Unit Test (Solutions): Some Applications of Trigonometry | Mathematics (Maths) Class 10 PDF Download
Time: 1 hour
M.M. 30
Attempt all questions.
- Question numbers 1 to 5 carry 1 mark each.
- Question numbers 6 to 8 carry 2 marks each.
- Question numbers 9 to 11 carry 3 marks each.
- Question number 12 & 13 carry 5 marks each.
Q1: _______________________ is drawn from the eye of an observer to the targeted object. (1 Mark)
(a) A parallel line
(b) Line of sight
(c) Elevation line
(d) Depression line
Ans: (b)
The line of sight is a line that is drawn from the eye of an observer to the targeted object viewed by the observer and the line of sight is required to form the angle of elevation.
Q2: A slope is built against a wall which makes an angle 30° with the ground and the height of the wall is 2 meters. Find the length of the slope in meters. (1 Mark)
a) 2
b) 4
c) 1
d) 3
Ans: (b)
AC is the length of the slope in ∆ABC.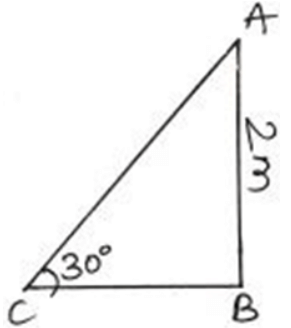
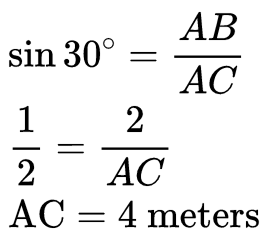
Q3: The shadow of a tower is equal to its height at 10-45 a.m. The sun’s altitude is (1 Mark)
(a) 30°
(b) 45°
(c) 60°
(d) 90°
Ans: (b)
Let the height of tower BC = x m and sun’s altitude = θ
Then Length of its shadow, AB = x m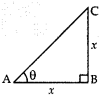 In rt. ∆ABC, tan θ = BC/AB = x/x = 1
In rt. ∆ABC, tan θ = BC/AB = x/x = 1
⇒ tan θ = tan 450
∴ θ = 45°
Q4: In given figure, the value of CE is (1 Mark)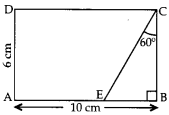
(a) 12 cm
(b) 6 cm
(c) 9 cm
(d) 6√3 cm
Ans: (a)
In rt. ∆EBC, cos 60° = BC/CE
⇒
1/2 = 6/CE
⇒
CE = 12cm
Q5: When the length of shadow of a vertical pole is equal to √3 times of its height, the angle of elevation of the Sun’s altitude is __________________________. (1 Mark)
Ans: 30°
Let the height of the vertical pole, BC = h m
∴ Shadow AB = √3h m and the angle of elevation angle BAC = θ 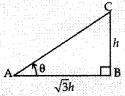
In rt ∆ABC, tan θ = BC/AB = h/√3h = 1/√3 = tan 30°
∴ θ = 30°
Hence the Sun’s altitude is 30°.
Q6: The ratio of the height of a tower and length of its shadow on the ground is √3 : 1 what is the angle of elevation of the sun? (2 Marks)
Ans: Let TW be tower and WS be its shadow.
Let ∠TSW = θ (angle of elevation)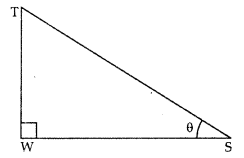
tanθ = √3/1
θ=60∘
Therefore, the angle of elevation of the sun is 60º.
Q7: A ladder, leaning against a wall, makes an angle of 60° with the horizontal. If the foot of the ladder is 2.5 m away from the wall, find the length of the ladder. (2 Marks)
Ans: Let AC be the ladder and the foot C is 2.5 m away from the wall AB.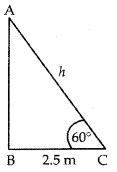
cos 60° = BC/AC = 2.5/h
1/2 = 2.5/h
h = 5m
Q8: An observer 1.5 m tall is 28.5 m away from a tower of height 30 m. Find the angle of elevation of the top of tower from his eye. (2 Marks)
Ans: In right ∆ABC,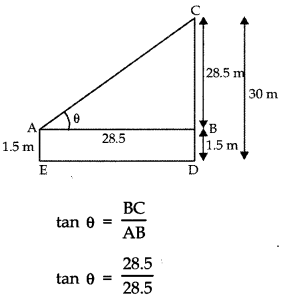
tan θ = 1 = tan 45°
θ = 45°
Q9: A moving boat is observed from the top of a 150 m high cliff moving away from the cliff. The angle of depression of the boat changes from 60° to 45° in 2 minutes. Find the speed of the boat in m/h. (3 Marks)
Ans: Let C & D be two positions of the boat,& AB be the cliff & let speed of boat be xm/ min.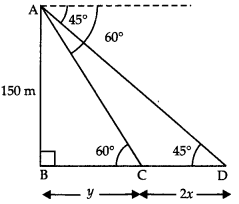 Let BC = y
Let BC = y
∴ CD = 2x (∵ Distance = speed × time) 
Q10: The angle of elevation of the top of a hill at the foot of a tower is 60° and the angle of elevation of the top of the tower from the foot of the hill is 30°. If height of the tower is 50 m, find the height of the hill. (3 Marks)
Ans: Let HL be Hill and TW be Tower angle of elevations ∠WLT = 30°
∠ LWH = 60°, let WL = x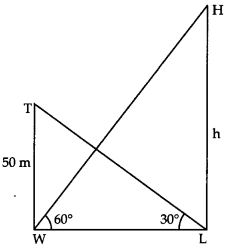 In ΔWLT, use tan30º to find x
In ΔWLT, use tan30º to find x
tan30º = 50/x
⇒ x = 50√3 ……. (i)
In rt. ∠d ∆WLH
⇒ h/x = tan 60°
⇒ h = 50√3 × √3 = 150 [Using (i)]
∴ Height of hill = 150 m
Q11: A man standing on the deck of a ship, which is 10 m above water level, observes the angle of elevation of the top of a hill as 60° and the angle of depression of the base of hill as 30°. Find the distance of the hill from the ship and the height of the hill. (3 Marks)
Ans:
Let AB be height of ship’s deck and CD be hill with C as top and D as base. Here angle of elevation ∠CAE = 60°.
Draw AE ⊥ CD and angle of depression ∠EAD = 30°
Let AE = BD = x
CE = y and ED = 10
Also, ∠BDA = ∠EAD = 30° [alternate angles]
In ∆ABD 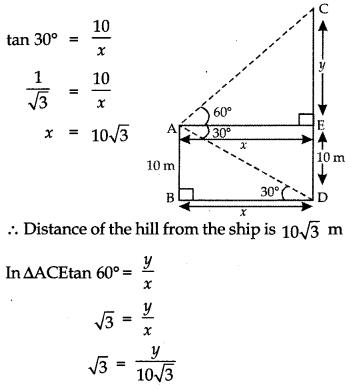
Now, CD = x + y
⇒ CD = 30 + 10 = 40 m
∴ The height of the hill is 40m.
Q12: At the foot of a mountain the elevation of its summit is 45°, after ascending 1000 m towards the mountain up a slope of 30° inclination, the elevation is found to be 60°. Find the height of the mountain. (5 Marks)
Ans: 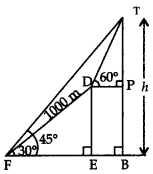 Let F be the foot and T be the summit of the mountain TFH such that ∠TFH = 45°
Let F be the foot and T be the summit of the mountain TFH such that ∠TFH = 45°
∴ In right ∆TBF,
∠BTF = 90° – 45° = 45°
Let height of mountain be h i.e., TB = h
since ∠TFH = ∠BTF = 45° ⇒ BF = BT = h
∠DFE = 30° and FD = 1000 m, ∠TDP = 60°
Draw DE ⊥BF and DP ⊥ BT
In right ∆DEF,
cos 30° = FE/DF = √3/2 = FE/1000
⇒ FE = 500√3 m
Also sin 30° = DE/DF = 1/2 = DE/1000
⇒ DE = 500 m
∴ BP = DE ⇒ BF = 500 m
Now TP = TB – BP = h – 500
In right ∆TPD, 
Q13: The angles of elevation and depression of the top and the bottom of a tower from the top of a building, 60 m high, are 30° and 60° respectively. Find the difference between the heights of the building and the tower and the distance between them. (5 Marks)
Ans: In right ∆ABE, 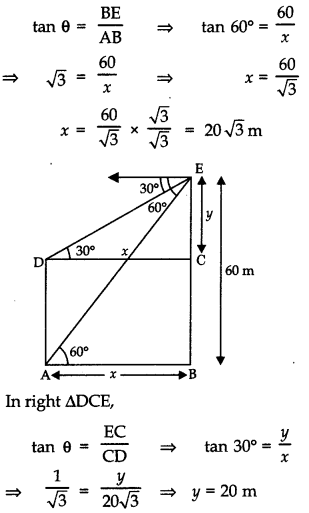
∴ Difference between heights of the building and tower = y = 20 m
Distance between tower and building = x
= 20√3 m
|
129 videos|736 docs|84 tests
|
FAQs on Unit Test (Solutions): Some Applications of Trigonometry - Mathematics (Maths) Class 10
| 1. What are some real-life applications of trigonometry in hobbies? |  |
| 2. How can trigonometry help in navigation for outdoor hobbies? |  |
| 3. What role does trigonometry play in designing models for hobbies like model building? |  |
| 4. Can trigonometry be used in digital hobbies such as gaming or animation? |  |
| 5. How does trigonometry enhance the experience in outdoor activities like climbing or cycling? |  |
















