Unit Test Solutions: A Tale of Three Intersecting Lines | Mathematics (Ganita Prakash) Class 7 - New NCERT PDF Download
Time: 1 hour
M.M. 30
Attempt all questions.
Question numbers 1 to 5 carry 1 mark each.
Question numbers 6 to 8 carry 2 marks each.
Question numbers 9 to 11 carry 3 marks each.
Question number 12 & 13 carry 5 marks each.
Q1: If two angles of a triangle are 35° and 85°, what is the measure of the third angle? (1 Mark)
a) 50°
b) 60°
c) 70°
d) 80°
Ans: b) 60°
The sum of the angles in a triangle is always 180°.
Third angle = 180° - (35° + 85°) = 180° - 120° = 60°.
Q2: In triangle XYZ, the exterior angle at Y is 140°, and ∠X = 65°. What is the measure of ∠Z? (1 Mark)
a) 75°
b) 80°
c) 85°
d) 90°
Ans: a) 75°
The exterior angle at a vertex of a triangle equals the sum of the two remote interior angles. For triangle XYZ, the exterior angle at Y is 140°, and the remote interior angles are ∠X and ∠Z. Thus:
140° = ∠X + ∠Z
140° = 65° + ∠Z
∠Z = 140° - 65° = 75°.
Q3. In a triangle DEF, if ∠D = 50° and ∠E = 60°, can a triangle be formed with these angles and a side DE of 7 cm? (1 Mark)
a) Yes, because the sum of angles is less than 180°
b) No, because the sum of angles is equal to 180°
c) No, because the sum of angles is greater than 180°
d) Yes, but only if the side length is greater than 7 cm
Ans: a) Yes, because the sum of angles is less than 180°
A triangle can be formed if the sum of the given angles is less than 180°, allowing a third angle to complete the sum to 180°. Here:
50° + 60° = 110° < 180°.
The third angle is 180° - 110° = 70°. The side length of 7 cm does not affect the angle condition, so a triangle can be formed.
Q4: Which of the following sets of side lengths cannot form a triangle? (1 Mark)
a) 7 cm, 8 cm, 10 cm
b) 4 cm, 4 cm, 8 cm
c) 6 cm, 9 cm, 14 cm
d) 5 cm, 12 cm, 13 cm
Sol: b) 4 cm, 4 cm, 8 cm
Using the triangle inequality theorem, the sum of any two sides must be greater than the third side. Checking each option:
- a) 7 + 8 = 15 > 10, 7 + 10 = 17 > 8, 8 + 10 = 18 > 7 (passes)
- b) 4 + 4 = 8 = 8 (not greater than, fails)
- c) 6 + 9 = 15 > 14, 6 + 14 = 20 > 9, 9 + 14 = 23 > 6 (passes)
- d) 5 + 12 = 17 > 13, 5 + 13 = 18 > 12, 12 + 13 = 25 > 5 (passes)
Option b fails because the sum of two sides equals the third, which does not satisfy the strict inequality required.
Q5. If two sides of a triangle are 6 cm and 8 cm, what is the minimum integer length of the third side? (1 Mark)
a) 7 cm
b) 4 cm
c) 3 cm
d) 5 cm
Sol: 3 cm
The triangle inequality requires 6 + x > 8, so x > 2.
The smallest integer is 3 cm.
Q6. In triangle XYZ, if ∠X = 90° and ∠Y = 45°, what is the measure of ∠Z? (2 Mark)
Sol: 45°.
Explanation: The sum of angles in a triangle is 180°. Given ∠X = 90° and ∠Y = 45°:
∠Z = 180° - (90° + 45°) = 180° - 135° = 45°.
Q7. Find the exterior angle at vertex B in triangle ABC if angle A = 40 degrees and angle C = 60 degrees. (2 Mark)
Sol: 100°.
First, angle B = 180° - (40° + 60°) = 80°.
The exterior angle at B is 180° - 80° = 100°.
Q8. In triangle XYZ, if angle X = angle Y and angle Z = 50 degrees, what is angle X? (2 Mark)
Sol: 65°.
Since angle X = angle Y, let each be x.
Angle sum: x + x + 50° = 180°.
Thus, 2x = 130°
⇒ x = 65°
Q9. Find the value of the unknown angle: (3 Mark)

Sol: In ∆PQR, ∠PRS = ∠PQR + ∠QPR
So, 140° = x + 120°
x = 140° – 120°
x = 20°
Q10. Find the third angle of a triangle when two of the angles are 45° and 80°. (3 Mark)
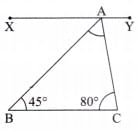
Sol:
Here ∠B = 45° and ∠C = 80°.
Since the line BC is parallel to XY.
So, ∠XAB = ∠B = 45°
[Alternate angles] … (i)
and ∠YAC = ∠C = 80°
[Alternate angles] … (ii)
Also, ∠XAB + ∠BAC + ∠YAC = 180°
⇒ 45° + ∠BAC + 80° = 180° [Using (i) and (ii)]
⇒∠BAC = 180° – 125°
= 55°.
Q11. In triangle LMN, if angle L = 50 degrees and angle M = 70 degrees, find the exterior angle at vertex N and determine its relationship with angles L and M. (3 Mark)
Sol: First, find angle N using the angle sum property: Angle L + Angle M + Angle N = 180 degrees.
Substituting, 50 + 70 + Angle N = 180.
This simplifies to 120 + Angle N = 180,
so Angle N = 60 degrees.
The exterior angle at N is supplementary to Angle N: Exterior angle = 180 - 60 = 120 degrees.
To find the relationship, note that the exterior angle at N equals the sum of the opposite interior angles (L and M):
50 + 70 = 120 degrees.
Thus, the exterior angle at N is 120 degrees, and it equals the sum of angles L and M.
Q12. In triangle UVW, if angle U = 45 degrees and angle V = 60 degrees, find the third angle W and determine the ratio of angles U, V, and W. (5 Mark)
Sol: To find angle W in triangle UVW and the ratio of angles U, V, and W, we proceed as follows:
Calculate Angle W
Use the angle sum property: Angle U + Angle V + Angle W = 180 degrees.
Substitute: 45 + 60 + Angle W = 180.
Simplify: 105 + Angle W = 180.
Solve: Angle W = 180 - 105 = 75 degrees.
Determine Ratio of Angles
List angles: Angle U = 45 degrees, Angle V = 60 degrees, Angle W = 75 degrees.
Express ratio: 45 : 60 : 75.
Find the greatest common divisor: 45, 60, 75 are divisible by 15.
Simplify:
45 / 15 = 3.
60 / 15 = 4.
75 / 15 = 5.
Ratio: 3 : 4 : 5.
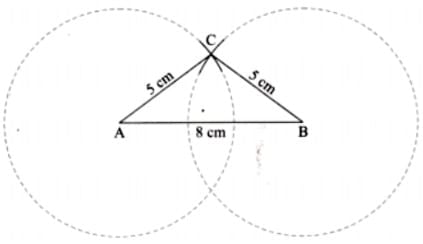
Q13. Construct a triangle having the side lengths 5, 5, and 8. (all units are in cm) (5 Mark)
Sol:Steps of Construction:
Step 1: Construct the base AB with one of the side lengths. Let us choose AB = 8 cm.
Step 2: From A, construct an arc of radius 5 cm.
Step 3: From B, construct an arc of radius 5 cm such that it intersects the first arc.
Step 4: The point where both the arcs meet is the required third vertex C. Join AC and BC to get ∆ABC.
|
41 videos|251 docs|8 tests
|
FAQs on Unit Test Solutions: A Tale of Three Intersecting Lines - Mathematics (Ganita Prakash) Class 7 - New NCERT
| 1. What are intersecting lines, and how are they defined in geometry? |  |
| 2. Can you explain the properties of intersecting lines? |  |
| 3. How can intersecting lines be represented in a coordinate plane? |  |
| 4. What is the significance of intersecting lines in real-world applications? |  |
| 5. How can one identify the intersection point of two lines algebraically? |  |