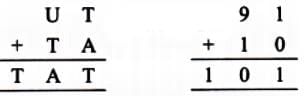Unit Test Solutions: Number Play | Mathematics (Ganita Prakash) Class 7 - New NCERT PDF Download
Time: 1 hour
M.M. 30
Attempt all questions.
- Question numbers 1 to 5 carry 1 mark each.
- Question numbers 6 to 8 carry 2 marks each.
- Question numbers 9 to 11 carry 3 marks each.
- Question number 12 & 13 carry 5 marks each.
Q1.What is the parity of the sum of an odd number of odd numbers and an even number of even numbers? (1 Mark)
A) Always odd
B) Always even
C) Depends on the specific numbers chosen
D) Sometimes odd, sometimes even
Sol: A) Always odd
An odd number of odd numbers sums to an odd number (e.g., 1 + 3 + 5 = 9, odd). An even number of even numbers sums to an even number (e.g., 2 + 4 = 6, even). Adding an odd number to an even number results in an odd sum (odd + even = odd).
Q2. What is the parity of the number of small squares in a 7 × 9 grid? (1 Mark)
A) Even
B) Odd
C) Depends on the grid layout
D) Cannot be determined
Sol: B) Odd
The number of squares is 7 × 9 = 63. Since 7 and 9 are both odd, odd × odd = odd. Thus, the parity is odd.
Q3. In a cryptarithm where X + X = YX, where X and Y are digits and YX is a two-digit number, what is the value of Y? (1 Mark)
A) 0
B) 1
C) 2
D) 3
Sol: B) 1
2X = YX means 2X = 10Y + X.
Subtract X: X = 10Y.
Since X and Y are digits, Y = 1, X = 10 (not a digit).
Testing: X = 5, 2 × 5 = 10, YX = 10 (Y = 1). Thus, Y = 1.
Q4. How many ways can 5 be expressed as a sum of 1s and 2s (e.g., 1+1+1+1+1, 2+1+2)? (1 Mark)
A) 5
B) 8
C) 7
D) 13
Sol: B) 8
The number of ways to write n as a sum of 1s and 2s is the (n+1)th Virahanka-Fibonacci term.
For n = 5, the 6th term is 8 (1, 2, 3, 5, 8, 13, …).
Q5. In the Virahanka-Fibonacci sequence (1, 2, 3, 5, 8, 13, …), what is the parity of the 9th term? (1 Mark)
A) Odd
B) Even
C) Depends on the starting terms
D) Cannot be determined
Sol: A) Odd
The 9th term in the sequence is 55 (1, 2, 3, 5, 8, 13, 21, 34, 55). Since 55 ÷ 2 leaves a remainder of 1, it is odd.
Q6. In the Virahanka-Fibonacci sequence (1, 2, 3, 5, 8, 13, …), what is the parity of the 8th term? (2 Mark)
Sol: Even
The 8th term is 34 (sequence: 1, 2, 3, 5, 8, 13, 21, 34). Since 34 ÷ 2 = 17, it is even
Q7. What is the 20th odd number in the sequence 1, 3, 5, 7, …? (2 Mark)
Sol: 39
The nth odd number is 2n - 1. For n = 20, 2 × 20 - 1 = 40 - 1 = 39.
Q8. What is the parity of the number of small squares in a 5 × 8 grid? (2 Mark)
Sol: Even
The number of squares is 5 × 8 = 40. Since 5 is odd and 8 is even, odd × even = even. Thus, the parity is even.
Q9. In a cryptarithm where K + K = MK, where K and M are digits and MK is a two-digit number, what is the value of M? (3 Mark)
Sol: 1
2K = MK means 2K = 10M + K.
Subtract K: K = 10M.
Since K and M are digits,
M = 1, K = 10 (not a digit).
Testing: K = 5, 2 × 5 = 10, MK = 10 (M = 1).
Thus, M = 1.
Q10. A door is initially locked. Tashi toggles the lock 50 times, where each toggle switches the door’s state (from locked to unlocked or unlocked to locked). Will the door be locked or unlocked at the end? Explain why. (3 Mark)
Sol: Tashi toggles the lock 50 times.
Each toggle changes the door’s state (locked to unlocked or unlocked to locked).
Starting from locked:
An odd number of toggles will leave the door unlocked, and an even number of toggles will leave it locked.
Since 50 is even, after 50 toggles, the door will be locked.
Q1. Solve this cryptarithm: (3 Mark)
Sol: Here, T is at the hundreds place, so T = 1
⇒ A = 0 and U = 9.
So, we have U = 9, T = 1, and A = 0.
Q12. Arjun has an odd number of ₹1 coins, an odd number of ₹5 coins, and an even number of ₹10 coins in his piggy bank. He calculated the total and got ₹205. Did he make a mistake? If he did, explain why. If he didn’t, how many coins of each type could he have? (5 Mark)
Sol: He made a mistake.
Odd ₹1 coins give an odd amount;
Odd ₹5 coins give an odd multiple of 5 (odd); even ₹10 coins give an even amount.
Odd + odd + even = odd. Since 205 is an odd number, the total of ₹ 205 is not possible with an odd number of ₹ 1 and ₹ 5 coins and an even number of ₹ 10 coins
Q13. Two consecutive numbers in the Virahānka sequence are 987 and 1597. What are the next 2 numbers in the sequence? What are the previous 2 numbers in the sequence? (5 Mark)
Sol: The given numbers are 987 and 1597.
In the Virahanka sequence, each number is the sum of the two preceding numbers.
The next two numbers are:
987 + 1597 = 2584
1597 + 2584 = 4181
The previous two numbers are:
1597 – 987 = 610
987 – 610 = 377
The sequence is …..,377, 610, 987, 1597, 2584, 4181,…..
|
41 videos|251 docs|8 tests
|
FAQs on Unit Test Solutions: Number Play - Mathematics (Ganita Prakash) Class 7 - New NCERT
| 1. What are the key concepts covered in the Number Play curriculum for Class 7? |  |
| 2. How can I effectively prepare for the Number Play unit test? |  |
| 3. Are there any specific types of questions commonly found in the Number Play unit test? |  |
| 4. What strategies can help with solving word problems in Number Play? |  |
| 5. How important is it to understand the properties of numbers in the Number Play curriculum? |  |