Unit Test Solutions: Parallel and Intersecting Lines | Mathematics (Ganita Prakash) Class 7 - New NCERT PDF Download
Time: 1 hour
M.M. 30
Attempt all questions.
- Question numbers 1 to 5 carry 1 mark each.
- Question numbers 6 to 8 carry 2 marks each.
- Question numbers 9 to 11 carry 3 marks each.
- Question number 12 & 13 carry 5 marks each.
Directions: Questions 1–5 refer to the figure below. For each given pair of lines, identify whether they are parallel, perpendicular, or intersecting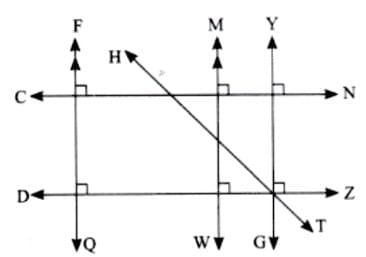
Q1. Lines FQ and HT are ___________ lines. (1 Mark)
Sol: Lines FQ and HT are intersecting lines.
Q2. Lines FQ and MW are ___________ lines. (1 Mark)
Sol: Lines FQ and MW are parallel lines.
Q3. Lines CN and FQ are ___________ lines. (1 Mark)
Sol: Lines CN and FQ are perpendicular lines.
Q4. Lines DZ and YG are ___________ lines. (1 Mark)
Sol: Lines DZ and YG are perpendicular lines,
Q5. Lines CN and YG are ___________ lines. (1 Mark)
Sol: Lines CN and YG are perpendicular lines.
Q6. Write down each pair of adjacent angles shown in the following figure (2 Mark)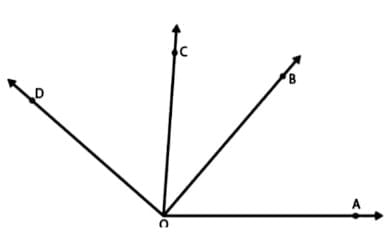
Sol:
The angles that have common vertex and a common arm are known as adjacent angles
Therefore the adjacent angles in the given figure are:
∠DOC and ∠BOC
∠DOB and ∠BOA
∠COB and ∠BOA
∠AOC and ∠COD
Q7. In given figure, if ∠c is 120°, figure out the measurements of ∠a, ∠b, and ∠d, without drawing and measuring them? (2 Mark)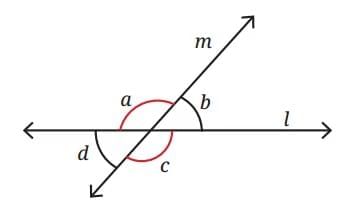
Sol: ∠d = 180° - ∠c
∠d = 180° - 120° = 60° (linear pair).
∠c = ∠a = 120° (vertically opposite).
∠d = ∠b = 60° (vertically opposite).
Q8. Two angles form a straight line. One angle measures 102°. What is the other? (2 Mark)
Sol: Angles on a straight line add up to 180° (linear pair).
So,
180° − 102° = 78°
Q9. State which lines are parallel and why? (3 Mark)
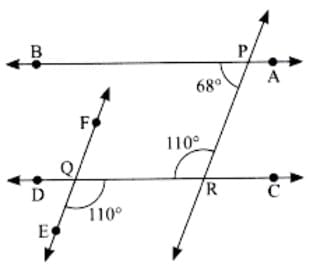
Sol: If a transversal intersects two lines such that a pair of alternate interior angles is equal, then the two lines are parallel.
Since ∠EQR = ∠PRQ =110° and lines FE and PR are intersected by a transversal DC such that the pair of alternate angles is equal.
So, FE || PR.
Q10.List all the linear pairs and vertically opposite angles you observe in Figure. (3 Mark)
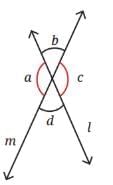
Sol: Linear Pairs: These are angles that are adjacent and form a straight line (add up to 180°).
- ∠a and ∠b
- ∠b and ∠c
- ∠c and ∠d
- ∠d and ∠a
Vertically Opposite Angles: These are angles that are opposite each other when two lines intersect (they are equal).
- ∠b and ∠d (they are opposite each other at the intersection).
- ∠a and ∠c (they are opposite each other at the intersection).
Q11. Find the measure of angle 'a' and angle 'b'. (3 Mark)
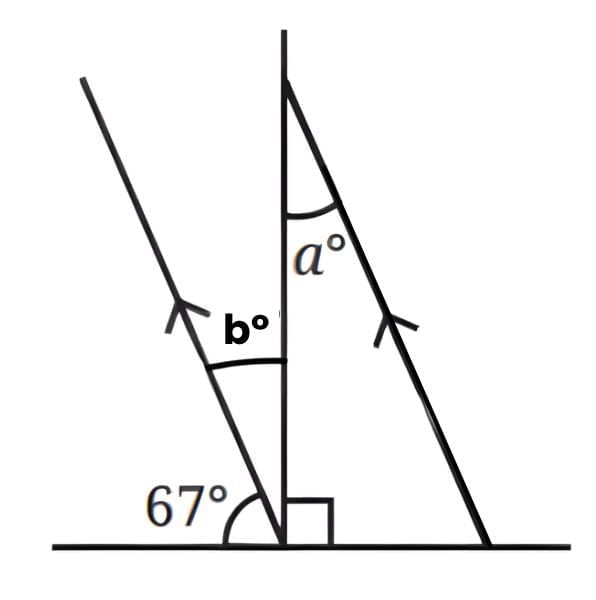
Sol:
⇒ 67° + bº + 90° = 180° ( Using angles on a straight line)
⇒ bº = 180° - 67° = 23°
⇒ a° = bº ( Also, alternate angles are equal).
⇒ bº = 23°
Q12. In the given figure, l || m and t is a transversal. If ∠1 = 55°, find ∠2, ∠3, ∠4, ∠5, ∠6, ∠7 and ∠8. (5 Mark)

Sol:
Since l || m and ∠1 = 55°
So, ∠3 = ∠1 = 55° (Vertically opposite angles)
and ∠1 + ∠2 = 180° (Linear pair)
or, ∠2 = 180° – ∠1 = 180° – 55° = 125°
Also, ∠5 = ∠3 = 55° (Alternate interior angles)
Now, ∠4 + ∠5 = 180°
(Interior angles on the same side of the transversal)
or ∠4 = 180° – ∠5 = 180° – 55° = 125°
Also, ∠6 = ∠2 = 125° (Corresponding angles)
Now ∠5 = ∠7 = 55° (Vertically opposite angles)
Also, ∠6 = ∠8 = 125° (Vertically opposite angles)
Hence, ∠2 = 125°, ∠3 = 55°, ∠4 = 125°, ∠5 = 55°, ∠6 = 125°, ∠7 = 55° and ∠8 = 125°.
Q13. Find whether the lines AB and CD are parallel or not. (5 Mark)
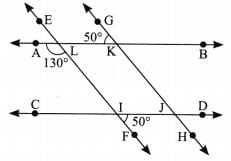
Sol:
∠CIF + ∠FIJ = 180° [Linear pair]
∠CIF = 180° - ∠FIJ
= 180° - 50°= 130°
So, ∠ALI = ∠CIF = 130° .
If two parallel lines are intersected by a transversal, then each pair of corresponding angles are equal.
Here, ∠ALI = ∠CIF = 130° are two corresponding angles.
Hence, AB || CD
|
41 videos|251 docs|8 tests
|
FAQs on Unit Test Solutions: Parallel and Intersecting Lines - Mathematics (Ganita Prakash) Class 7 - New NCERT
| 1. What are parallel lines and how can they be identified? |  |
| 2. What are intersecting lines and how do they differ from parallel lines? |  |
| 3. Can two lines be both parallel and intersecting at the same time? |  |
| 4. How does the concept of parallel and intersecting lines apply in real life? |  |
| 5. What are the angle relationships formed by intersecting lines? |  |






















