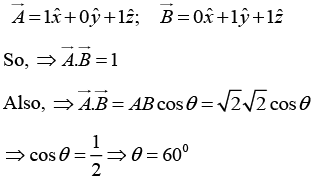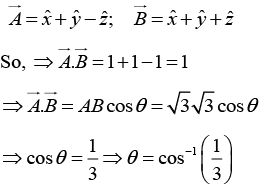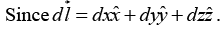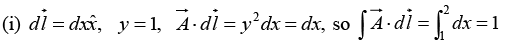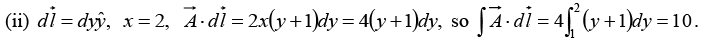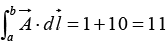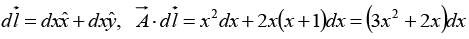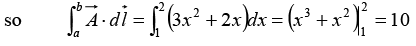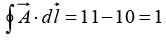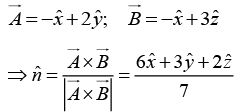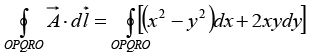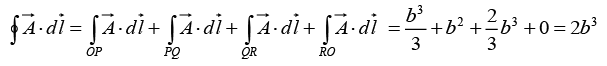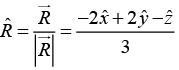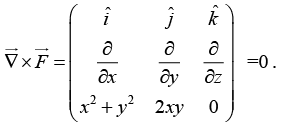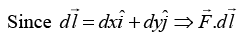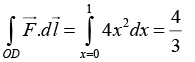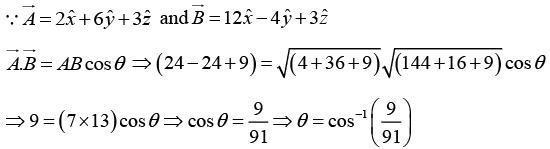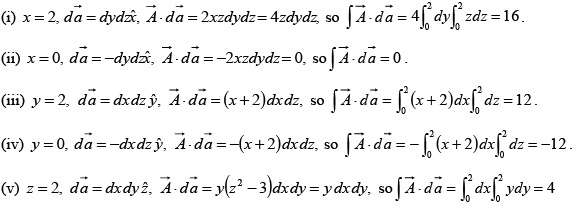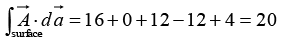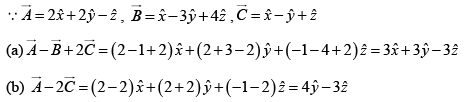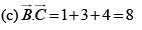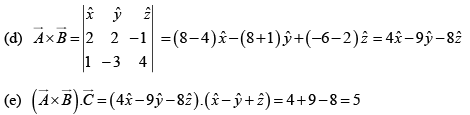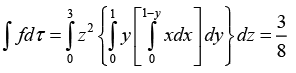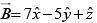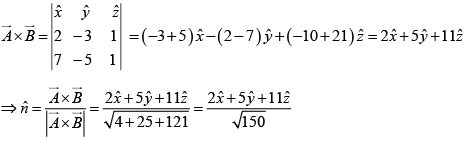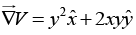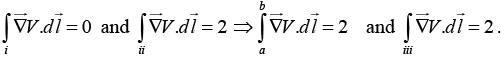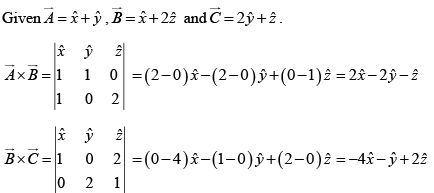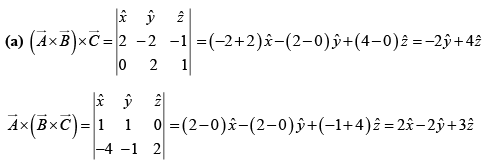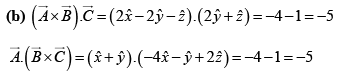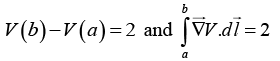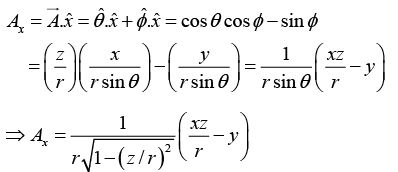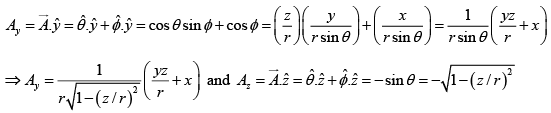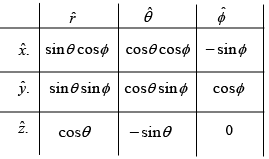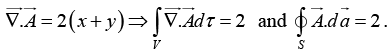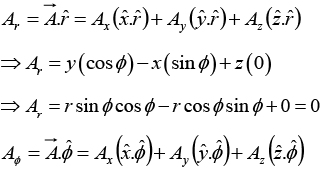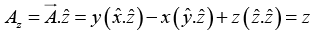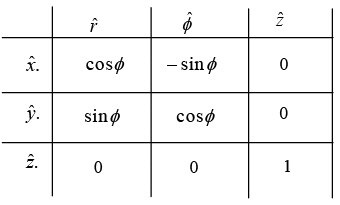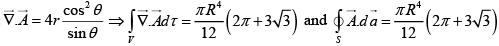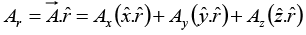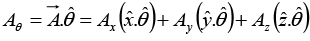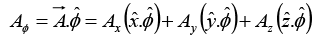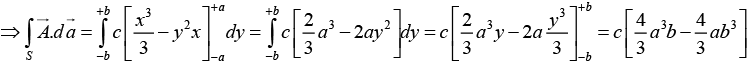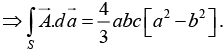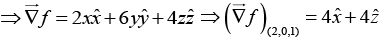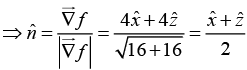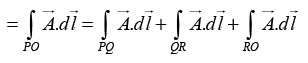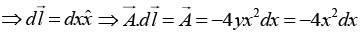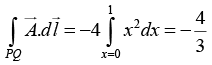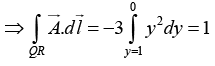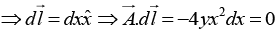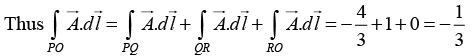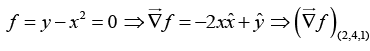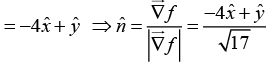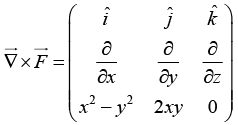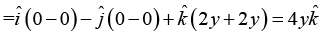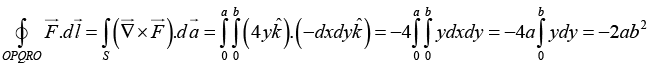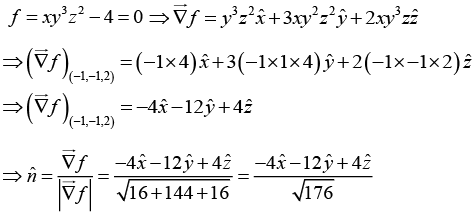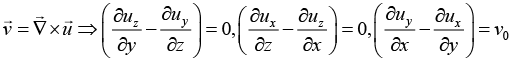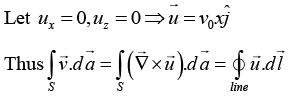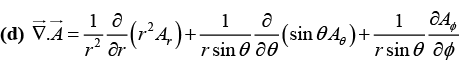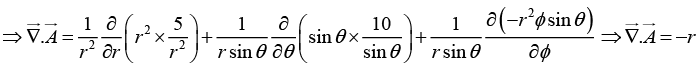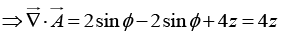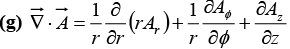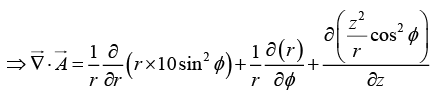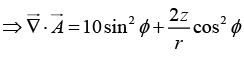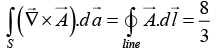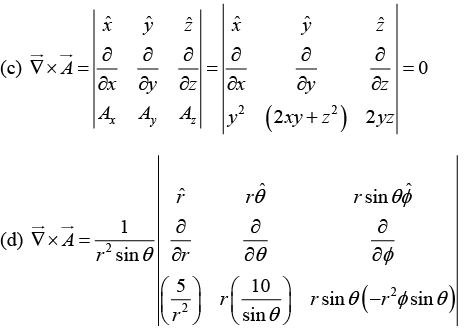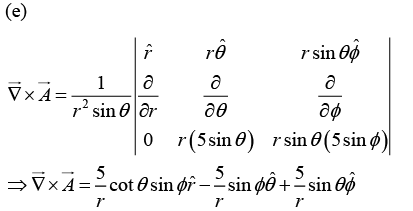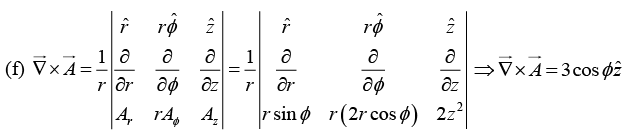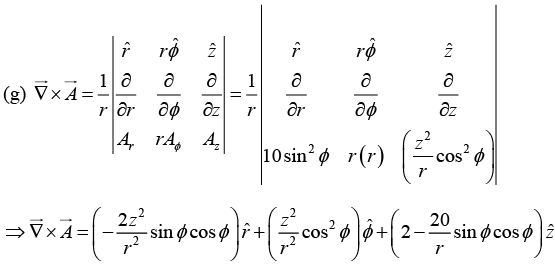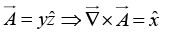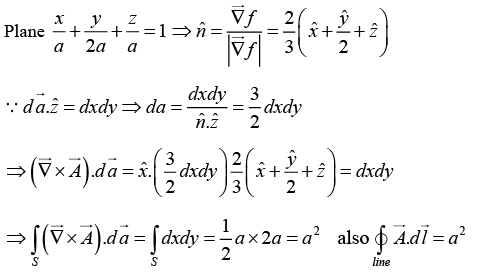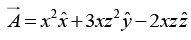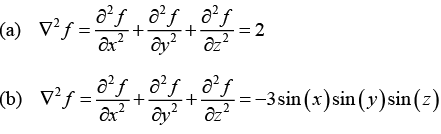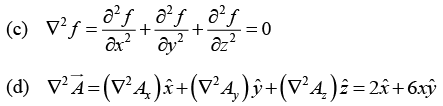Vector Analysis: Assignment | Mathematical Methods - Physics PDF Download
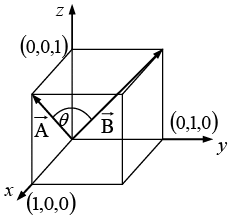
Q.1. (a) Find the angle between the face diagonals of a cube of unit length.
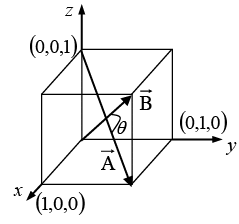
(b) Find the angle between the body diagonals of a cube of unit length.

(a) The face diagonals
are
(b) The body diagonals
are
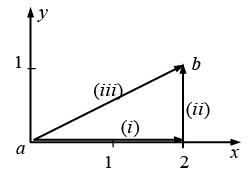
Q.2. Calculate the line integral of the function 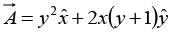 from the point a = (1, 1, 0) to the point b = (2, 2, 0) along the paths (1) and (2) as shown in figure. What is
from the point a = (1, 1, 0) to the point b = (2, 2, 0) along the paths (1) and (2) as shown in figure. What is 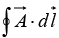 for the loop that goes from a to b along (1) and returns to a along (2)?
for the loop that goes from a to b along (1) and returns to a along (2)?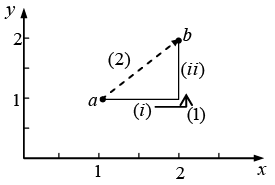
Path (1) consists of two parts. Along the “horizontal” segment dy = dz = 0, so
On the “vertical” stretch dx = dz = 0, so
By path (1), then,
Meanwhile, on path (2) x = y, dx = dy, and dz = 0, so
For the loop that goes out (1) and back (2), then,
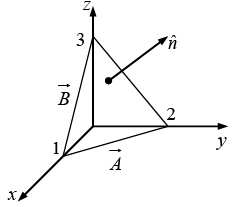
Q.3. Find the components of the unit vector nˆ perpendicular to the plane as shown in the figure.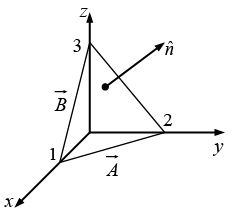
The vectors
can be defined as
Q.4. Find the line integral of the vector  around a square of side ‘b’ which has a corner at the origin, one side on the x axis and the other side on the y axis.
around a square of side ‘b’ which has a corner at the origin, one side on the x axis and the other side on the y axis.
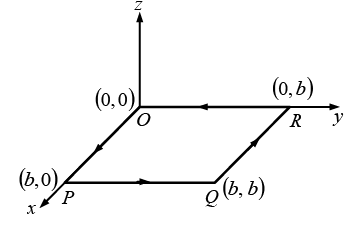
In a Cartesian coordinate system
Q.5. Find the separation vector  from the source point (2,8,7) to the field point (4,6,8). Determine its magnitude
from the source point (2,8,7) to the field point (4,6,8). Determine its magnitude 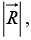 and construct the unit vector
and construct the unit vector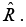
The separation vector
from the source point (2,8,7) to the field point (4,6,8) is
Its magnitudeand the unit vector
Q.6. (a) Determine whether the force represented by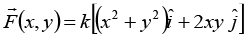 is conservative or not. Here k = 1Nm-2.
is conservative or not. Here k = 1Nm-2.
(b) Calculate the work done by this force in moving a particle from the origin O (0, 0, 0) to the point D(1, 1, 0) on the z = 0 plane along the paths OABD and OD as shown in the figure, where the coordinates are measured in meters.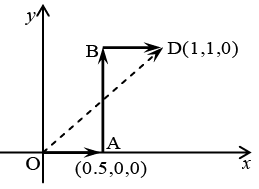
Thus the force
is conservative. So work done is independent of paths.
Along line OD , y = x ⇒ dy = dx
= [(x2 + y2) dx + 2xy dy] = [(x2 + x2) dx + 2x2dx] = 4x2dx
Q.7. Find the angle between vectors 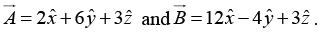
Q.8. Calculate the surface integral of  over five sides (excluding the bottom) of the cubical box (side 2) as shown in figure. Let “upward and outward” be the positive direction, as indicated by the arrows.
over five sides (excluding the bottom) of the cubical box (side 2) as shown in figure. Let “upward and outward” be the positive direction, as indicated by the arrows.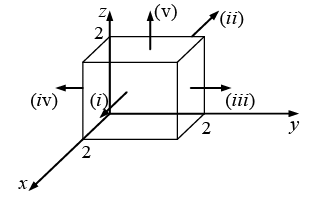
Taking the sides one at a time:
Evidently the total flux is
Q.9. For given vectors 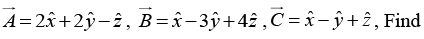
(a) 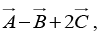
(b) The unit vector along 
(c) 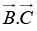
(d) 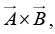
(e) 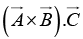
The unit vector along
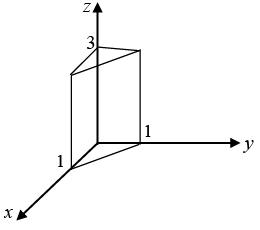
Q.10. Calculate the volume integral of f = xyz2 over the prism shown in the figure.
Q.11. Find the unit vector perpendicular to both of the vectors 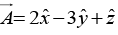 and
and 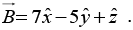
The vectors
can be defined as
and
Q.12. Let V = xy2, and take point a to be the origin (0, 0, 0) and b the point (2, 1, 0). Check the fundamental theorem for gradients.
V(b) - V(a) = 2
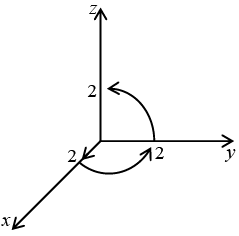
Q.13. (a) 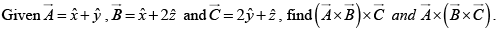
(b) Using the same vectors 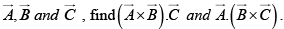
Q.14. Compute the gradient and Laplacian of the function T = r (cos θ + sin θ cos θ). Check the Laplacian by converting T to Cartesian coordinates. Test the gradient theorem for this function, using the path shown in figure, from (0, 0, 0) to (0, 0, 2).
T = r (cos θ + sin θ cos ϕ) = z + x ⇒ ∇2T = 0
Q.15. Transform the vector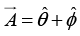 into Cartesian Coordinates.
into Cartesian Coordinates.
x = r sinθ cosϕ , y = r sinθ sinϕ , z = r cosϕ
Q.16. Check the divergence theorem using the function 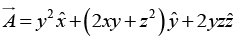 and the unit cube situated at the origin.
and the unit cube situated at the origin.
Q.17. Transform the vector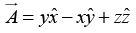 into Cylindrical Coordinates.
into Cylindrical Coordinates.
x = r cosϕ , y =r sinϕ , z = z
⇒ Aϕ = y (-sinϕ) - x (cos ϕ) + z (0) = -r sin2 ϕ - r cos2 ϕ = -r
Q.18. Check the divergence theorem for the function
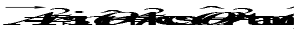
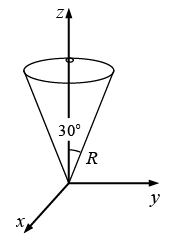
using the volume of the “ice-crem cone” shown in the figure.
(The top surface is spherical, with radius R and centered at the origin)
Q.19. Transform the vector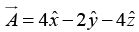 into spherical polar Coordinates.
into spherical polar Coordinates.
x = r sinθ cosϕ , y = r sinθ sinϕ , z = r cosθ
⇒ Ar = 4(sinθ cosϕ) - 2 (sinθ sinϕ) - 4 (cosθ)⇒ Ar = 2 sinθ [2cosϕ - sinϕ] - 4 (cosθ)
⇒ Aθ = 4(cosθ cosϕ) - 2 (cosθ sinϕ) - 4 (- sinθ)⇒ Aθ = 2 cosθ[2cosϕ - sinϕ] + 4 sinθ
⇒ Aϕ = 4 (-sinϕ) - 2 (cosϕ) - 4(0) = -4 sinϕ - 2 cosϕ
Q.20. For the vector field 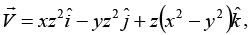
(a) Calculate the volume integral of the divergence of 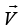 out of the region defined by a ≤ x ≤ a, -b ≤ y ≤ b and 0≤ z ≤ c.
out of the region defined by a ≤ x ≤ a, -b ≤ y ≤ b and 0≤ z ≤ c.
(b) Calculate the flux of 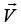 out of the region through the surface at z = c. Hence deduce the net flux through the rest of the boundary of the region.
out of the region through the surface at z = c. Hence deduce the net flux through the rest of the boundary of the region.
Thus
(b) The flux ofout of the region through the surface at z = c is
Q.21. Find a unit vector normal to the surface x2 + 3y2 + 2z2 = 6 at P (2, 0,1).
f = x2 + 3y2 + 2z2 - 6 = 0
Q.22. Consider a vector 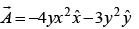
(a) Calculate the line integral 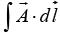 from point P→O along the path P→Q→R→O as shown in the figure.
from point P→O along the path P→Q→R→O as shown in the figure.
(b) Using Stokes’s theorem appropriately, calculate 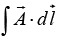 for the same path P→Q→R→O.
for the same path P→Q→R→O.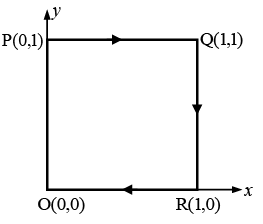
The line integral
from point P → O is
Along line PQ , y = 1 ⇒ dy = 0
Along line QR , x = 1 ⇒ dx = 0
Along line RO , y = 0 ⇒ dy = 0
Q.23. Find the unit vector normal to the curve y = x2 at the point (2, 4, 1).
Q.24. How much work is done when an object moves from O → P → Q → R → O in a force field given by 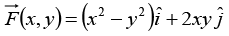 along the rectangular path shown. Find the answer by evaluating the line integral and also by using the Stokes’ theorem.
along the rectangular path shown. Find the answer by evaluating the line integral and also by using the Stokes’ theorem.
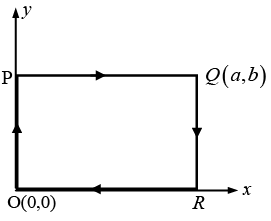
Using the Stokes’ theorem
Q.25. Find the unit vector normal to the surface xy3z2 = 4 at a point (-1, -1, 2).
Q.26. (a) Consider a constant vector field 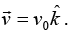 Find any one of the many possible vectors
Find any one of the many possible vectors 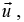 for which
for which 
(b) Using Stoke’s theorem, evaluate the flux associated with the field 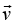 through the curved hemispherical surface defined by x2 + y2 + z2 = r2, z > 0.
through the curved hemispherical surface defined by x2 + y2 + z2 = r2, z > 0.
We have to take line integral around circle x2 + y2 = r2 in z = 0 plane. Let use cylindrical coordinate and use x = r cosϕ , y = r sinϕ ⇒ dy = r cosϕdϕ.
Q.27. Calculate the divergence of the following vector functions:
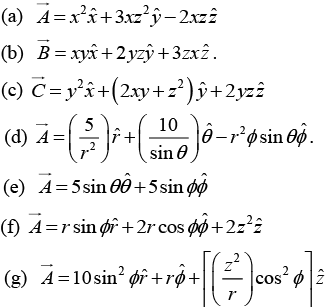
Q.28. Compute the line integral of 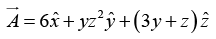 along the triangular path shown in figure. Check your answer using Stoke’s theorem.
along the triangular path shown in figure. Check your answer using Stoke’s theorem.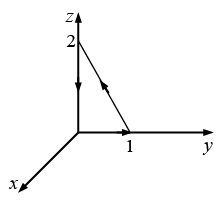
Q.29. Calculate the curls of the following vector functions: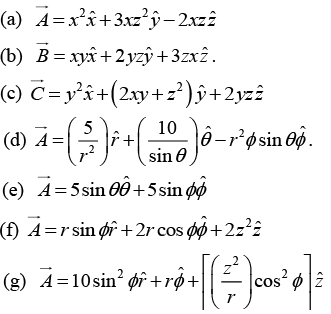
Q.30. Check Stoke’s theorem for the function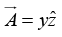 using the triangular surface shown in figure below.
using the triangular surface shown in figure below.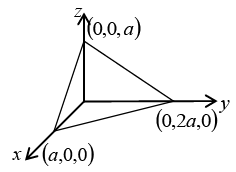
Q.31. Calculate the Laplacian of the following functions:
(a) f(x, y, z) = x2 + 2xy + 3z + 4
(b) f(x, y, z) = sin(x) sin(y) sin(z)
(c) f(x, y, z) = e-5x sin4y cos3z 
|
78 videos|18 docs|24 tests
|
FAQs on Vector Analysis: Assignment - Mathematical Methods - Physics
| 1. What is vector analysis? |  |
| 2. How is vector analysis used in IIT JAM? |  |
| 3. What are the key concepts covered in vector analysis for IIT JAM? |  |
| 4. How can I improve my understanding of vector analysis for IIT JAM? |  |
| 5. Are there any real-life applications of vector analysis? |  |