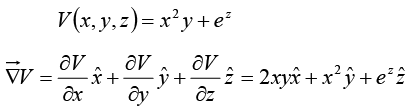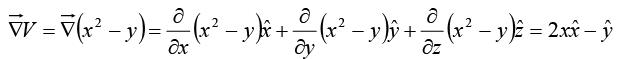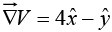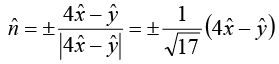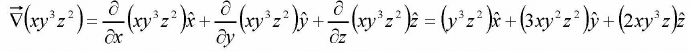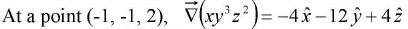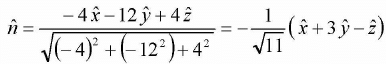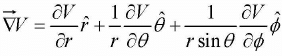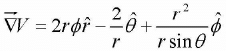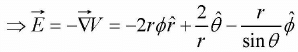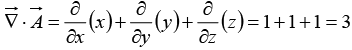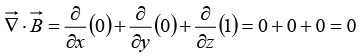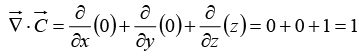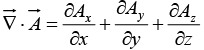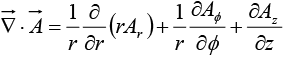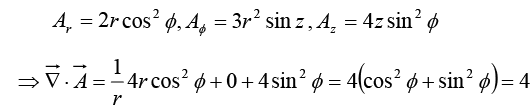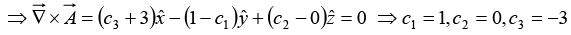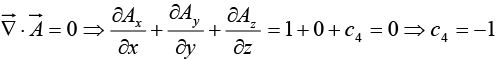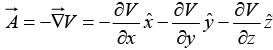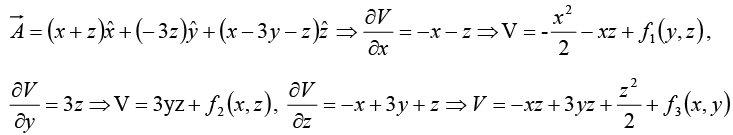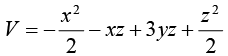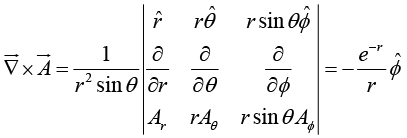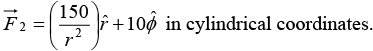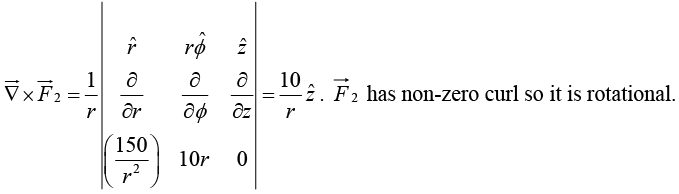Differential Calculus | Mathematical Methods - Physics PDF Download
“Ordinary” Derivatives
- We have a function that depends on one variable, which we can call f(x).
- The derivative of this function, noted as df/dx, shows us how quickly the function f(x) changes when we make a small adjustment to the input x.
- When we change the value of x by a tiny amount, known as dx, the derivative helps us understand the rate of that change in the function.
- In simpler terms, the derivative tells us the slope of the function at any point, indicating whether the function is increasing or decreasing.
- If the derivative is positive, it means that as x increases, the function f(x) is also increasing.
- Conversely, if the derivative is negative, the function is decreasing as x increases.
- If the derivative equals zero, it suggests that the function has a flat point at that location, meaning it is neither increasing nor decreasing at that instant.
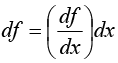
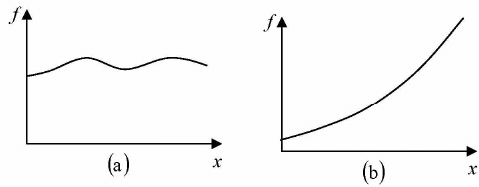
In words: If we change x by an amount dx, then f changes by an amount df the derivative is the proportionality factor. For example in figure (a), the function varies slowly with x, and the derivative is correspondingly small. In figure (b), f increases rapidly with x, and the derivative is large, as we move away from x = 0.
Geometrical Interpretation:The derivative d f / dx is the slope o f the graph off versus x.
Gradient
Suppose that we have a function of three variables-say, V(x, y, z) in a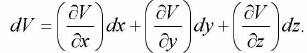
This tells us how V changes when we alter all three variables by the infinitesimal amounts dx, dy, dz. Notice that we do not require an infinite number o f derivatives-three will suffice: the partial derivatives along each of the three coordinate directions.
Thus 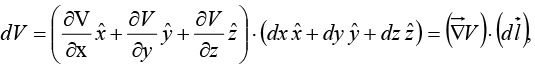
where  is the gradient of V .
is the gradient of V . is a vector quantity, with three components.
is a vector quantity, with three components.
Geometrical Interpretation of the Gradient
Like any vector, the gradient has magnitude and direction. To determine its geometrical meaning, let’s rewrite
where θ is the angle between  and
and . Now, i f we fix the magnitude
. Now, i f we fix the magnitude and search around in various directions (that is, varyθ), the maximum change in V evidently occurs when θ = 0(for then cos θ = 1). That is, for a fixed distance
and search around in various directions (that is, varyθ), the maximum change in V evidently occurs when θ = 0(for then cos θ = 1). That is, for a fixed distance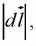 dT is greatest when one move in the same direction as
dT is greatest when one move in the same direction as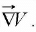 Thus:
Thus:
The gradient 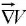 points in the direction of maximum increase of the function F.
points in the direction of maximum increase of the function F.
Moreover:
The magnitude gives the slope (rate o f increase) along this maximal direction.
gives the slope (rate o f increase) along this maximal direction.
Gradient in Spherical polar coordinates: V (r,θ,∅)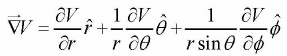
Gradient in cylindrical coordinates:V (r,∅,z)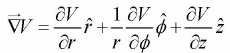
Example 4: Find the gradient of a scalar function of position V where V(x,y, z) = x2y + e2. Calculate the magnitude of the gradient at point P(1, 5,-2).
Example 5: Find the unit vector normal to the curve = x2 at the point (2, 4, 1).
The equation of curve in the form of surface is given by
x2 - y = 0
A constant scalar function V on the surface is given by V (x,y,z) =x2 -y
Taking the gradient
The value of the gradient at point (2, 4, 1),
The unit vector, as required
Example 6: Find the unit vector normal to the surface xy3z2 = 4 at a point (-1, -1, 2).
Unit vector normal to the surface
Example 7: In electrostatic field problems, the electric field is given b y 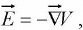 , where F V s the scalar field potential. If V = r2∅ - 2θ in spherical coordinates, then find
, where F V s the scalar field potential. If V = r2∅ - 2θ in spherical coordinates, then find 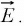
F = r2∅ - 2θ
In spherical coordinate,
Substituting the suitable values,
The Operator 
The gradient has the formal appearance of a vector,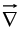 , “multiplying” a scalar V:
, “multiplying” a scalar V: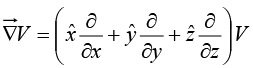
The term in parentheses is called “del”: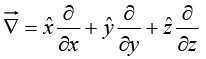
We should say that 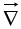 is a vector operator that acts upon V, not a vector that multiplies V.There are three ways the operator
is a vector operator that acts upon V, not a vector that multiplies V.There are three ways the operator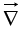 can act:
can act:
1. on a scalar function V: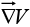 (the gradient);
(the gradient);
2. on a vector function 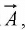 via the dot product:
via the dot product: 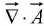 (the divergence),
(the divergence),
3. on a vector function 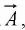 via the cross product:
via the cross product: 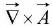 (the curl).
(the curl).
Divergence
From the definition of 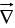 we construct the divergence:
we construct the divergence: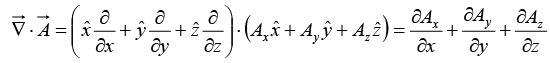
Observe that the divergence of a vector function 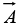 is itself a scalar
is itself a scalar 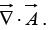 (You can't have the divergence of a scalar: that’s meaningless.)
(You can't have the divergence of a scalar: that’s meaningless.)
Geometrical Interpretation
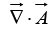 is a measure of how much the vector
is a measure of how much the vector 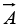 spreads out (diverges) from the point in question. For example, the vector function in figure (a) has a large (positive) divergence (if the arrows pointed in, it would be a large negative divergence), the function in figure (b) has zero divergence, and the function in figure (c) again has a positive divergence. (Please understand that
spreads out (diverges) from the point in question. For example, the vector function in figure (a) has a large (positive) divergence (if the arrows pointed in, it would be a large negative divergence), the function in figure (b) has zero divergence, and the function in figure (c) again has a positive divergence. (Please understand that 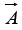 here is a function-there’s a different vector associated with every point in space.)
here is a function-there’s a different vector associated with every point in space.)
(a)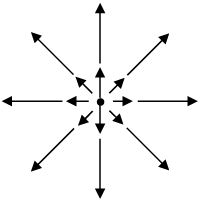
(b)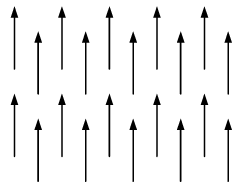
(c)
Divergence in Spherical polar coordinates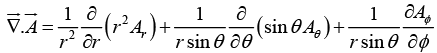
Divergence in cylindrical coordinates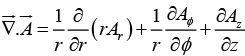
Example 8: Suppose the function sketched in above figure are 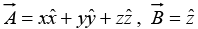 and
and  Calculate their divergences.
Calculate their divergences.
Example 9: Given
(i)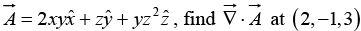
(ii)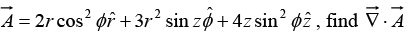
(iii)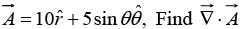
(i) In Cartesian coordinates,
(ii) In cylindrical coordinates
(iii) In spherical coordinates,
The Curl
From the definition of
 we construct the curl
we construct the curl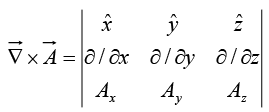
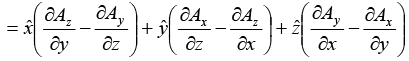
Notice that the curl of a vector function
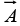 is, like any cross product, a vector. (You cannot have the curl of a scalar; that’s meaningless.)
is, like any cross product, a vector. (You cannot have the curl of a scalar; that’s meaningless.)Geometrical Interpretation
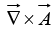 is a measure of how much the vector
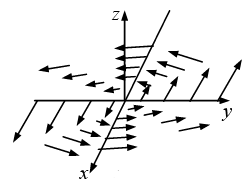
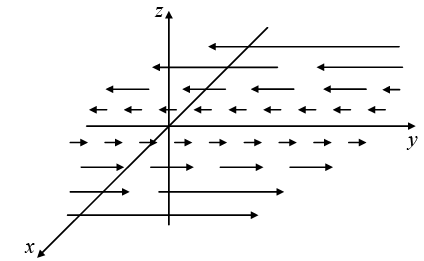
is a measure of how much the vector 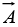 ‘‘curls around” the point in question. Figure shown below have a substantial curl, pointing in the z-direction, as the natural right-hand rule would suggest.
‘‘curls around” the point in question. Figure shown below have a substantial curl, pointing in the z-direction, as the natural right-hand rule would suggest.
(a)
(b)
Curl in Spherical polar coordinates
Curl in cylindrical coordinates
Example 10: Suppose the function sketched in above figure are 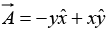 and
and 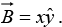
Calculate their curls.
As expected, these curls point in the +z direction. (Incidentally, they both have zero divergence, as you might guess from the pictures: nothing is “spreading out”.... it just “curls around.”)
Example 11: Given a vector function 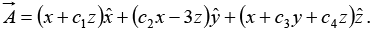
(a) Calculate the value of constants c1,c2,c3 if 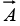 is irrotational.
is irrotational.
(b) Determine the constant c4 if 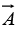 is also solenoidal.
is also solenoidal.
(c) Determine the scalar potential function V, whose negative gradient equals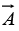 .
.
(a) If A is irrotational then,
(b) Ifis solenoidal,
(c)
Examination of above expressions of V gives a general value of
Example 12: Find the curl of the vector 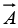 = (e-r/r)
= (e-r/r)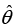
= (e-r/r)
⇒Ar = 0, Aθ = (e-r/r), AФ =0
Example 13: Find the nature of the following fields by determining divergence and curl.
(i) 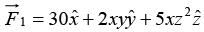
(ii) 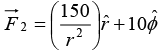 (Cylindrical coordinates)
(Cylindrical coordinates)
(i)
Divergence exists, so the field is non-solenoidal.The field has a curl so it is rotational.
(ii)
In cylindrical coordinates, DivergenceThe field is non-solenoid.
Product Rules
The calculation of ordinary derivatives is facilitated by a number of general rules, such as
the sum rule: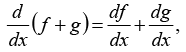
the rule for multiplying by a constant: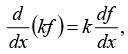
the product rule: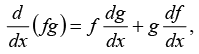
and the quotient rule: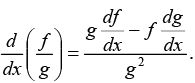
Similar relations hold for the vector derivatives. Thus,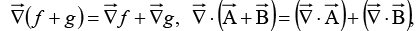
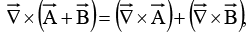
and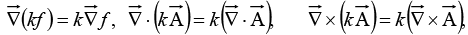
as you can check for yourself. The product rules are not quite so simple. There are two ways to construct a scalar as the product of two functions:
f g (product of two scalar functions),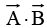 (Dot product of two vectors),
(Dot product of two vectors),
and two ways to make a vector: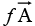 (Scalar time’s vector),
(Scalar time’s vector),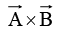 (Cross product of two vectors),
(Cross product of two vectors),
Accordingly, there are six product rules,
Two for gradients
(i) 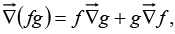
(ii) 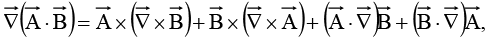
Two for divergences
(iii)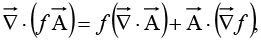
(iv)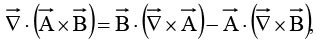
And two for curls
(v)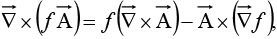
(vi)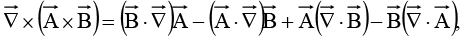
It is also possible to formulate three quotient rules: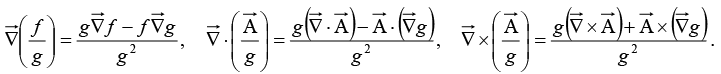
Second Derivatives
The gradient, the divergence, and the curl are the only first derivatives we can make with 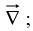 by applying
by applying twice we can construct five species of second derivatives. The gradient
twice we can construct five species of second derivatives. The gradient 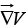 is a vector, so we can take the divergence and curl of it:
is a vector, so we can take the divergence and curl of it:
(1) Divergence of gradient: 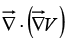
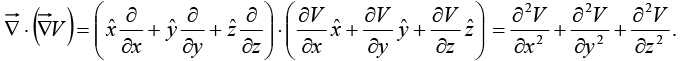 This object, which we write
This object, which we write  for short, is called the Laplacian of V. Notice that the Laplacian o f a scalar V is a scalar.
for short, is called the Laplacian of V. Notice that the Laplacian o f a scalar V is a scalar.
Laplacian in Spherical polar coordinates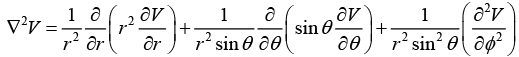
Laplacian in cylindrical coordinates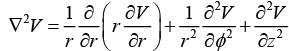
Occasionally, we shall speak o f the Laplacian o f a vector, 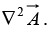 By this we mean a vector quantity whose x-component is the Laplacian of Ax, and so on:
By this we mean a vector quantity whose x-component is the Laplacian of Ax, and so on:
This is nothing more than a convenient extension of the meaning of 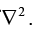 .
.
(2) Curl of gradient: 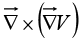
The divergence 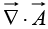 A is a scalar-all we can do is taking its gradient.
A is a scalar-all we can do is taking its gradient.
The curl of a gradient is always zero: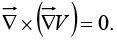
(3) Gradient of divergence: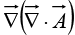
The curl 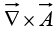 A is a vector, so we can take its divergence and curl.
A is a vector, so we can take its divergence and curl.
Notice that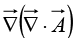 is not the same as the Laplacian of a vector:
is not the same as the Laplacian of a vector: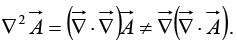
(4) Divergence of curl: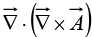
The divergence of a curl, like the curl of a gradient, is always zero: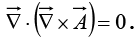
(5) Curl of curl: 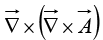
As you can check from the definition of 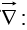
So curl-of-curl gives nothing new; the first term is just number (3) and the second is the Laplacian (of a vector).
|
78 videos|18 docs|24 tests
|
FAQs on Differential Calculus - Mathematical Methods - Physics
| 1. What is the importance of differential calculus in IIT JAM preparation? |  |
| 2. What are the basic concepts one should master in differential calculus for IIT JAM? |  |
| 3. How can I practice differential calculus effectively for IIT JAM? |  |
| 4. What types of questions related to differential calculus are commonly asked in IIT JAM? |  |
| 5. Are there any specific formulas I should memorize for differential calculus in IIT JAM? |  |