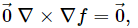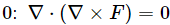Vector identities | Engineering Mathematics for Electrical Engineering - Electrical Engineering (EE) PDF Download
| Table of contents |

|
| Vector Linearity |

|
| Vanishing properties |

|
| Fundamental theorem of vector calculus |

|
| Solved Numericals |

|
The divergence, gradient, and curl satisfy several algebraic properties.
Let f and g denote scalar functions, R3→R and F and G be vector fields, R3→R3.
Vector Linearity
As with the sum rule of univariate derivatives, these operations satisfy: 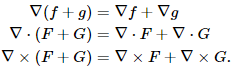
Product rule
The product rule (uv)′ = u′v + uv′ has related formulas: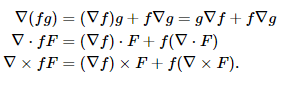 Rules over cross products
Rules over cross products
The cross product of two vector fields is a vector field for which the divergence and curl may be taken. There are formulas to relate to the individual terms: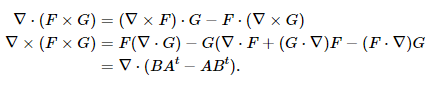 The curl formula is more involved.
The curl formula is more involved.
Vanishing properties
Surprisingly, the curl and divergence satisfy two vanishing properties. FirstThe curl of a gradient field is
if the scalar function f is has continuous second derivatives (so the mixed partials do not depend on order).
Vector fields where F = ∇f are conservative. Conservative fields have path independence, so any line integral, 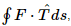 , around a closed loop will be 0. But the curl is defined as a limit of such integrals, so it too will be 0 Vector. In short, conservative fields have no rotation.
, around a closed loop will be 0. But the curl is defined as a limit of such integrals, so it too will be 0 Vector. In short, conservative fields have no rotation.
What about the converse? If a vector field has zero curl, then integrals around infinitesimally small loops are 0. Does this also mean that integrals around larger closed loops will also be 0, and hence the field is conservative? The answer will be yes, under assumptions. But the discussion will wait for later.
The combination ∇⋅∇f is defined and is called the Laplacian. This is denoted Δf. The equation Δf = 0 is called Laplace's equation. It is not guaranteed for any scalar function f, but the f for which it holds are important.
Second,
The divergence of a curl field is
This is not as clear, but can be seen algebraically as terms cancel. First:
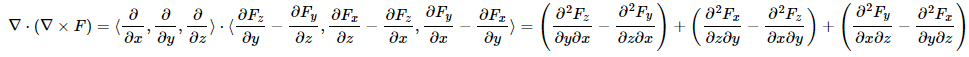 Focusing on one component function, Fz say, we see this contribution:
Focusing on one component function, Fz say, we see this contribution:
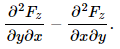
Fundamental theorem of vector calculus
The divergence and curl are complementary ideas. Are there other distinct ideas to sort a vector field by? The Helmholtz decomposition says not really. It states that vector fields that decay rapidly enough can be expressed in terms of two pieces: one with no curl and one with no divergence.Let F be a vector field on a bounded domain V which is twice continuously differentiable. Let S be the surface enclosing V. Then F can be decomposed into a curl-free component and a divergence-free component:
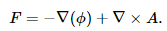 Without explaining why, these values can be computed using volume and surface integrals:
Without explaining why, these values can be computed using volume and surface integrals: 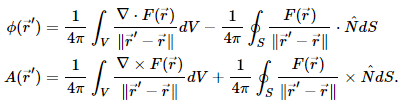
If V = R3 an unbounded domain, but Fvanishes faster than 1/r, then the theorem still holds with just the volume integrals:
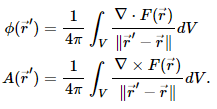 Change of Variable
Change of Variable
The divergence and curl are defined in a manner independent of the coordinate system, though the method to compute them depends on the Cartesian coordinate system. If that is inconvenient, then it is possible to develop the ideas in different coordinate systems.
We restrict to n = 3 and use (x, y, z) for Cartesian coordinates and (u, v, w) for an orthogonal curvilinear coordinate system, such as spherical or cylindrical. If 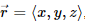 , then
, then The term
The term  is tangent to the curve formed by assuming v and w are constant and letting u vary. Similarly for the other partial derivatives. Orthogonality assumes that at every point, these tangent vectors are orthogonal.
is tangent to the curve formed by assuming v and w are constant and letting u vary. Similarly for the other partial derivatives. Orthogonality assumes that at every point, these tangent vectors are orthogonal.
As  is a vector it has a magnitude and direction. Define the scale factors as the magnitudes:
is a vector it has a magnitude and direction. Define the scale factors as the magnitudes:
 and let
and let 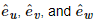 be the unit, direction vectors.
be the unit, direction vectors.
This gives the following notation: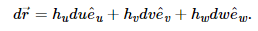 From here, we can express different formulas.
From here, we can express different formulas.
For line integrals, we have the line element:
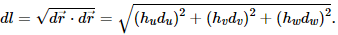 Consider the surface for constant u. The vector
Consider the surface for constant u. The vector 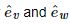 lie in the surface's tangent plane, and the surface element will be:
lie in the surface's tangent plane, and the surface element will be:
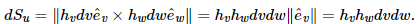 This uses orthogonality, so
This uses orthogonality, so 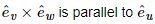 and has unit length. Similarly,
and has unit length. Similarly, 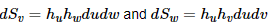
The volume element is found by projecting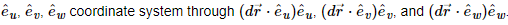 . Then forming the triple scalar product to compute the volume of the parallelepiped:
. Then forming the triple scalar product to compute the volume of the parallelepiped:
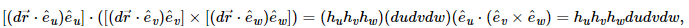 as the unit vectors are orthonormal, their triple scalar product is 1 and
as the unit vectors are orthonormal, their triple scalar product is 1 and 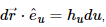 etc.
etc.
Solved Numericals
Q1. If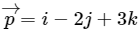 and
and 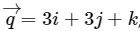 , then
, then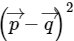 is equal to
is equal toSolution:
Concept Used:
for any vector,
Calculation:
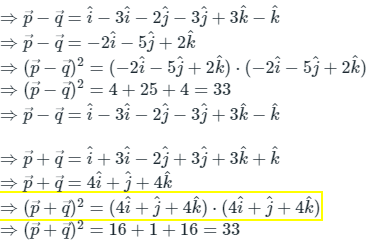
Q2. If A = 3i + j + k; B = 5i + j – k; C = i + j - k then find the volume of parallelogram if A, B, and C are the sides of the parallelepiped respectively.
Solution: A = 3i + j + k; B = 5i + j – k; C = i + j - k
The volume of parallelogram if A, B, and C are the sides of the parallelepiped
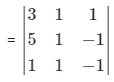
= 3(-1 + 1) +1(-1 + 5) +1(5 - 1)
= 0 + 4 + 4 = 8
Q3. If  inferior vector is,
inferior vector is, 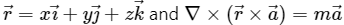 then m = will be__________ .
then m = will be__________ .
Solution: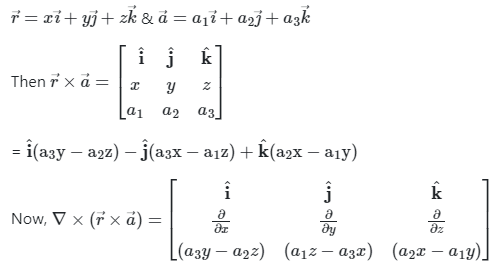
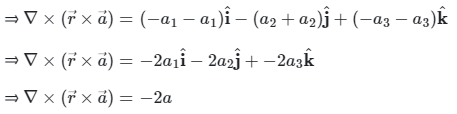
As given, 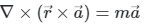
⇒ m = -2
|
44 videos|109 docs|58 tests
|
FAQs on Vector identities - Engineering Mathematics for Electrical Engineering - Electrical Engineering (EE)
| 1. What are vanishing properties in vector calculus? |  |
| 2. What is the fundamental theorem of vector calculus? |  |
| 3. How can vector identities be used in mechanical engineering? |  |
| 4. Can you provide an example of a solved numerical problem involving vector calculus? |  |
| 5. What are some common applications of the concepts discussed in vector calculus in real-world engineering scenarios? |  |