Class 9 Maths Chapter 1 Question Answers - Number System

Q1: Simplify: (√5 + √2)².
Ans:Here, (√5 + √2² = (√5² + 2√5√2 + (√2)²
= 5 + 2√10 + 2
= 7 + 2√10

Q2:How many rational numbers can be found between two distinct rational numbers?
(i) Two
(ii) Ten
(iii) Zero
(iv) Infinite
Ans: (iv) Infinite
Between any two distinct rational numbers, an infinite number of rational numbers can be found. This is because rational numbers are dense on the number line, meaning between any two rational numbers $a$a and b (a<b), you can always find another rational number by calculating the average:
New rational number = a+b/2 

Q3: Identify a rational number among the following numbers :
2 + √2, 2√2, 0 and π
Ans: 0 is a rational number.

Q4:  √8 is an
(i) natural number
(ii) rational number
(iii) integer
(iv) irrational number

Ans: (D) $\mathrm{<br\; style="word-break:\; break-word;\; line-height:\; 1.8;\; font-family:\; Lato,\; sans-serif;\; font-size:\; 20px;\; letter-spacing:\; inherit;\; color:\; black;">}\backslash sqrt\{8\}$√8 is an irrational number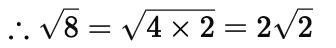

Q5: Find the value of √(3)^{- 2}.
Ans: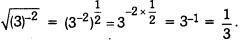


Q6:  Is zero a rational number? Can you write it in the form $\frac{p}{q}\backslash frac\{p\}\{q\}$, where $p$p and q are integers and $q\ne 0q\; \backslash neq\; 0$?

Ans: Consider the definition of a rational number. A rational number is the one that can be written in the form $\frac{p}{q}\backslash frac\{p\}\{q\}$ , where p and q are integers and $q\ne 0q\; \backslash neq\; 0$

Zero can be written as

$\frac{0}{1},\frac{0}{2},\frac{0}{3},\frac{0}{4},\frac{0}{5},\dots \backslash frac\{0\}\{1\},\; \backslash frac\{0\}\{2\},\; \backslash frac\{0\}\{3\},\; \backslash frac\{0\}\{4\},\; \backslash frac\{0\}\{5\},\; \backslash dots$

So, we arrive at the conclusion that $00$0 can be written in the form $\frac{p}{q}\backslash frac\{p\}\{q\}$, where $p$p is any integer.

Therefore, zero is a rational number.

Q7: A terminating decimal is

(i) a natural number
(ii) a rational number
(iii) a whole number
(iv) an integer.

Ans: (ii) a rational number

Q8: Find $64^\{\backslash frac\{1\}\{2\}\}$64^1/2
Ans:

Q9: Simplify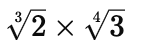

Ans: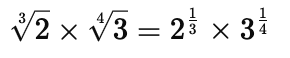The LCM of 3 and 4 is 12.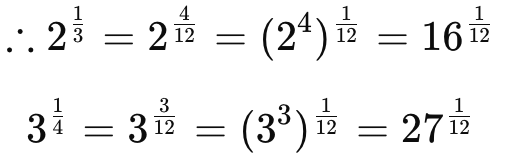

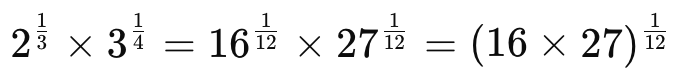
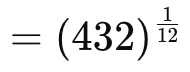
Q10: The sum of rational and an irrational number
(i) may be natural
(ii) may be irrational
(iii) is always irrational
(iv) is always rational

Ans: (iii) is always rational
Example: 
Rational number: $3$3
Irrational number: $2\backslash sqrt\{2$
Sum: $3+$√$2$
The sum $3+$√$23\; +\; \backslash sqrt\{2\}$ cannot be expressed as $\frac{p}{q}\backslash frac\{p\}\{q\}$, so it is irrational.