Pair of Linear Equations in Two Variables Class 10 Worksheet Maths Chapter 3
| Table of contents |

|
| A. Multiple Choice Questions |

|
| B. Fill in the blanks |

|
| C. Very Short Answer Questions |

|
| D. Short Answer Type Questions |

|
| E. Long Answer Type Questions |

|

A. Multiple Choice Questions
Q1: A pair of linear equations which have a unique solution x = 2, y = – 3 is:
(a) 2x – 3y = – 5, x + y = – 1
(b) 2x + 5y + 11 = 0, 4x + 10y + 22 = 0
(c) x – 4y – 14 = 0, 5x – y – 13 = 0
(d) 2x – y = 1, 3x + 2y = 0
Q2: If a system of a pair of linear equations in two unknowns is consistent, then the lines representing the system will be
(a) Parallel
(b) Always coincident
(c) Always intersecting
(d) Intersecting or coincident
Q3: The pair of equations x = 0 and y = 0 has
(a) One solution
(b) Two solutions
(c) Infinitely many solutions
(d) No solution
Q4: A pair of system of equations x = 2, y = -2; x = 3, y = – 3 when represented graphically enclose
(a) Square
(b) Trapezium
(c) Rectangle
(d) Triangle
Q5: If two lines are parallel to each other then the system of equations is
(a) Consistent
(b) Inconsistent
(c) Consistent dependent
(d) (a) and (c) both
B. Fill in the blanks
Q6: If in a system of equations corresponding to coefficients of member, equations are proportional then the system has ______________ solution (s).
Q7: A pair of linear equations is said to be inconsistent if its graph lines are ____________.
Q8: A pair of linear equations is said to be ____________ if its graph lines intersect or coincide.
Q9: A consistent system of equations where straight lines fall on each other is also called _____________ system of equations.
Q10: Solution of linear equations representing 2x – y = 0, 8x + y = 25 is ____________ .
C. Very Short Answer Questions
Q11: In Fig., ABCD is a rectangle. Find the values of x and y.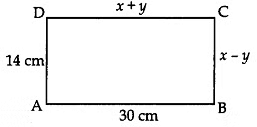
Q12: Graphically, determine whether the following pair of equations has no solution, a unique solution, or infinitely many solutions:
(1) 2x - 3y + 4 = 0
(2) 4x - 6y + 8 = 0
Q13: If 51x + 23y = 116 and 23x + 51y = 106, then find the value of (x – y).
Q14: For what value of V does the point (3, a) lie on the line represented by 2x – 3y = 5?
Q15: Determine whether the following system of linear equations is inconsistent or not.
3x – 5y = 20
6x – 10y = -40
D. Short Answer Type Questions
Q16: The father’s age is six times his son’s age. Four years hence, the age of the father will be four times his son’s age. Find the present ages of the son and the father.
Q17: If the lines x + 2y + 7 = 0 and 2x + ky + 18 = 0 intersect at a point, then find the value of k.
Q18: Find the value of k for which the system of equations x + 2y -3 = 0 and ky + 5x + 7 = 0 has a unique solution.
Q19: Find the values of a and b for which the following system of linear equations has an infinite number of solutions:
2x + 3 y = 7
2αx + (a + b) y = 28
Q20: In a cyclic quadrilateral ABCD, Find the four angles.
a. ∠A = (2 x + 4), ∠B = (y + 3), ∠C = (2y + 10) , ∠D = (4x − 5) .
b. ∠A = (2 x − 1) , ∠ B = (y + 5) , ∠C = (2 y + 15) and ∠D = (4 x − 7)
E. Long Answer Type Questions
Q21: Draw the graph of 2x + y = 6 and 2x – y + 2 = 0. Shade the region bounded by these lines and the x-axis. Find the area of the shaded region.
Q22: Draw the graphs of the following equations:
2x – y = 1, x + 2y = 13
(i) Find the solution of the equations from the graph.
(ii) Shade the triangular region formed by lines and the y-axis.
Q23: A man travels 370 km partly by train and partly by car. If he covers 250 km by train and the rest by car, it takes him 4 hours. But, if he travels 130 km by train and the rest by car, he takes 18 minutes longer. Find the speed of the train and that of the car.
Q24: The taxi charges in a city comprise a fixed charge together with the charge for the distance covered. For a journey of 10 km, the charge paid is ₹75 and for a journey of 15 km, the charge paid is ₹110. What will a person have to pay for traveling a distance of 25 km?
Q25: Solve the following system by drawing their graph:
(3/2)x – (5/4)y = 6, 6x – 6y = 20.
Determine whether these are consistent, inconsistent, or dependent.
You can access the solutions to this worksheet here.
|
127 videos|584 docs|79 tests
|
FAQs on Pair of Linear Equations in Two Variables Class 10 Worksheet Maths Chapter 3
| 1. What are the different methods to solve a pair of linear equations in two variables? |  |
| 2. How can we represent a pair of linear equations graphically? |  |
| 3. What is the significance of the solution of a pair of linear equations? |  |
| 4. What is the difference between consistent and inconsistent pairs of linear equations? |  |
| 5. Can a pair of linear equations have infinitely many solutions? If so, how? |  |





















