Class 7 Maths Chapter 7 Worksheet Solutions - A Tale of Three Intersecting Lines
| Table of contents |

|
| Section A: Multiple Choice Questions (MCQs) |

|
| Section B: Match the Following |

|
| Section C: Spot the Error |

|
| Section D: Think and Answer |

|
Section A: Multiple Choice Questions (MCQs)
Q1: Which of the following sets of side lengths can form a triangle?
a) 2 cm, 3 cm, 6 cm
b) 4 cm, 5 cm, 7 cm
c) 1 cm, 1 cm, 3 cm
d) 5 cm, 10 cm, 16 cm
Ans: b) 4 cm, 5 cm, 7 cm
Explanation: A triangle can be formed if the sum of any two sides is greater than the third side (triangle inequality). For option b:4 + 5 > 7 (9 > 7)
4 + 7 > 5 (11 > 5)
5 + 7 > 4 (12 > 4)
Other options fail at least one condition (e.g., for a: 2 + 3 = 5 < 6).
Q2 : If two angles of a triangle are 80° and 60°, what is the measure of the third angle?
a) 30°
b) 40°
c) 50°
d) 60°
Ans: b) 40°
Explanation: The sum of angles in a triangle is always 180°.
Thus, the third angle = 180° - (80° + 60°) = 180° - 140° = 40°.
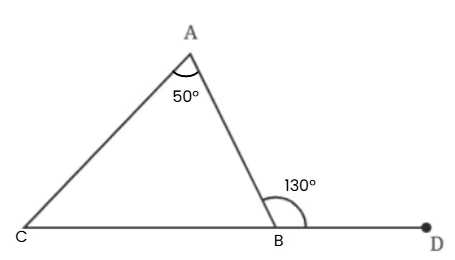
Q3: In triangle ABC, the exterior angle at B is 130°, and ∠A = 50°. The measure of ∠C is
a) 85°
b) 70°
c) 75°
d) 80°
Ans: d) 80°
Explanation: The exterior angle at B equals the sum of the remote interior angles (∠A and ∠C). Thus:
130° = 50° + ∠C
∠C = 130° - 50° = 80°.
Q4: In a triangle PQR, if ∠P = 45° and ∠Q = 75°, can a triangle be formed with these angles and an included side of 5 cm?
a) Yes, because the sum of angles is less than 180°
b) No, because the sum of angles is equal to 180°
c) No, because the sum of angles is greater than 180°
d) Yes, but only if the side length is greater than 5 cm
Ans: a) Yes, because the sum of angles is less than 180°
Explanation: A triangle can be formed if the sum of the given angles is less than 180°.
Here, 45° + 75° = 120° < 180°,
so a third angle (60°) exists to make the sum 180°.
Section B: Match the Following


Section C: Spot the Error
Q1: Isha wrote the following steps to construct a triangle:
Step 1: Draw AB = 6 cm
Step 2: At A, draw a 120° angle
Step 3: Mark a point C on the ray such that AC = 5 cm
Step 4: Join BC
She claims the triangle formed is equilateral.
Is she correct? Explain the mistake.
Ans: Mistake: She used an angle of 120°, which makes the triangle not equilateral.
In an equilateral triangle, all angles must be 60° and all sides equal.
Also, AB = 6 cm and AC = 5 cm are not equal.
Correction: Triangle is not equilateral.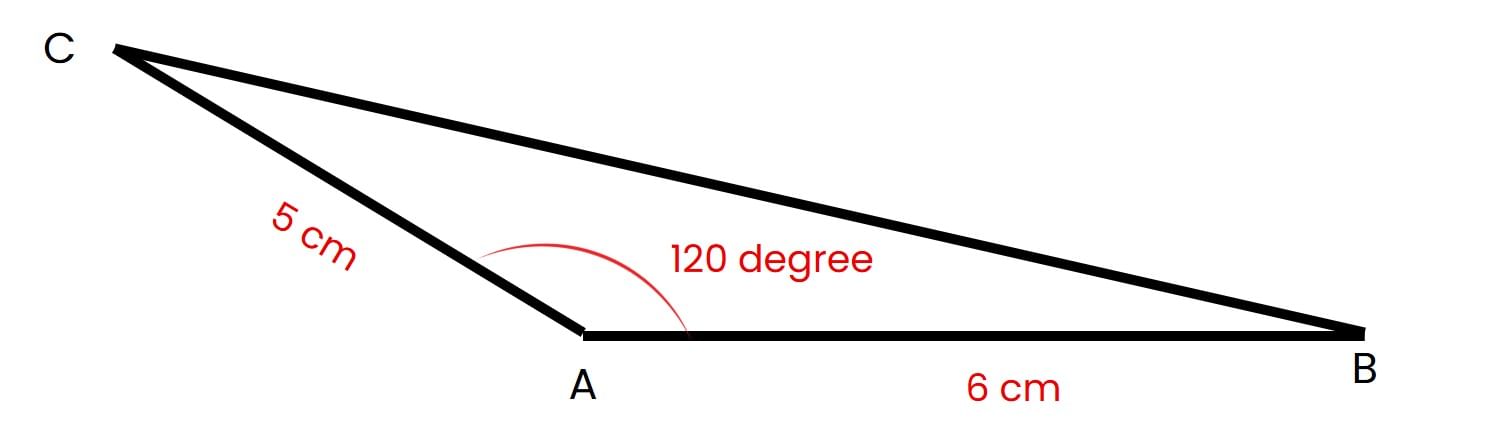
Section D: Think and Answer
Q1: A triangle has angles measuring 30°, 60°, and 90°.
a) Name the triangle based on its angles.
b) Will this triangle have an altitude inside or outside?
Ans: a) This triangle has one angle = 90°, which is a right angle.
So, it is called a Right-Angled Triangle.
b) In a right-angled triangle, all altitudes (heights) are usually drawn inside the triangle.
Since all angles are less than or equal to 90°, the altitude will lie inside the triangle.
Q2: A triangle has exactly one line of symmetry.
What kind of triangle is it and why?
Ans: A triangle with only one line of symmetry is an isosceles triangle.
In an isosceles triangle, two sides are equal, and the line of symmetry passes through the unequal side and the opposite angle.
That’s why it has only one line where you can fold it evenly.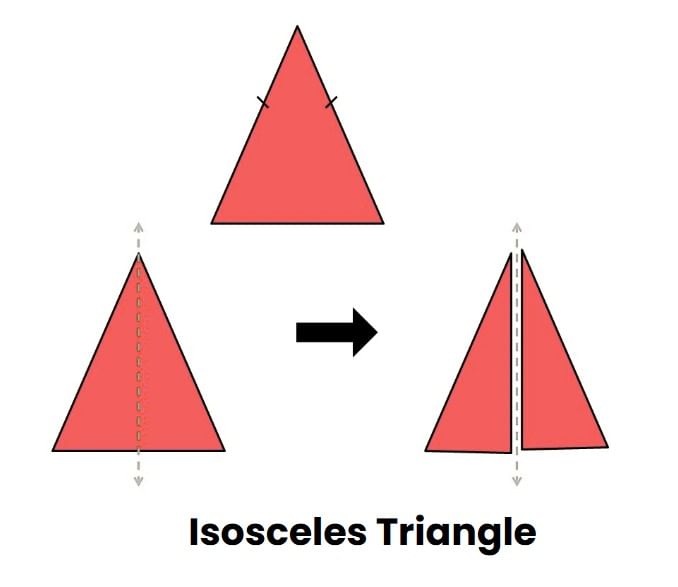
Q3: Can a triangle have:
a) All angles obtuse?
b) Two right angles?
Explain your answers.
Ans: a) No, a triangle cannot have all angles obtuse.
An obtuse angle is more than 90°.
If you add even two obtuse angles, the total will be more than 180°, which is not allowed in a triangle.
(Triangle angles must always add up to exactly 180°.)
b) No, a triangle cannot have two right angles.
Each right angle is 90°, and 90° + 90° = 180°, leaving no angle left for the third corner — and you need three angles in a triangle.
|
1 videos|107 docs
|
FAQs on Class 7 Maths Chapter 7 Worksheet Solutions - A Tale of Three Intersecting Lines
| 1. What are the key concepts covered in the worksheet "A Tale of Three Intersecting Lines"? |  |
| 2. How do I solve the multiple-choice questions in the worksheet effectively? |  |
| 3. What should I focus on while completing the fill-in-the-blanks section? |  |
| 4. Can you provide tips for tackling word problems related to intersecting lines? |  |
| 5. How can I prepare for an exam on the topic of intersecting lines and angles? |  |