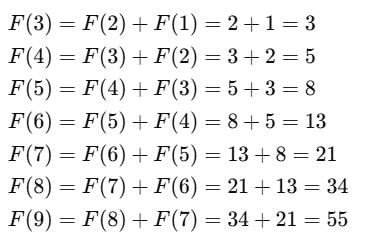Class 7 Maths Chapter 6 Worksheet Solutions - Number Play

Section A: Multiple Choice Questions

Q1: Two consecutive numbers in the Virahãnka sequence are 377 and 610. What is the first of the next 2 numbers?
A) 987
B) 1597
C) 2584
D) 4181

Ans: 987

Sol: 

In the Virahãnka-Fibonacci sequence:

Given 377 (Fn-1), 610 (Fn), compute:

Fn+1 = 377 + 610 = 987.

Fn+2 = 610 + 987 = 1597.
The next 2 numbers are 987, 1597. The first is 987. 
Verify: 233 + 377 = 610, 377 + 610 = 987. 

Q2: The expression 4n + 3 generates numbers for different values of n. What is the parity of 4n + 3 when n = 3?
A) 0
B) 1
C) 2
D) 4

Ans: 1
Solution:
For n = 3: 
4n + 3 = 4 × 3 + 3 = 12 + 3 = 15. 
Check parity: 15 ÷ 2 = 7.5 (odd, parity = 1). 

Q3: Anil wants to find the parity of the 10th term of the Virahãnka sequence. What is the parity?
A) 0
B) 1
C) 2
D) 3

Ans:  The Virahãnka-Fibonacci sequence is: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ... Parities (odd = 1, even = 0): 
1, 0, 1, 1, 0, 1, 1, 0, 1, 1. 
The pattern repeats every 3 terms: odd, even, odd (1, 0, 1). 
For the 10th term: 10 ÷ 3 = 3 remainder 1, so it corresponds to the 1st position in the cycle (odd, 1). 
Compute the 10th term: 89 (9th: 55, 10th: 55 + 34 = 89). 
Check: 89 ÷ 2 = 44.5 (odd). Parity = 1. Answer: B) 1.

Section B: Fill in the Blanks 

Q4: Solve the cryptarithm: X4 + Y = Z11. The value of X is ______.

Ans: 

X4 + Y = Z11: X4 (X tens, 4 units), Y (units), Z11 (Z hundreds, 1 tens, 1 units). 
Solve:

Units: 4 + Y = 1 (or 11 with carry).

Tens: X + carry = 1 (or 11).

Hundreds: 0 + carry = Z.
Units: 4 + Y = 11, so Y = 7. Carry 1. Tens: X + 1 = 1, so X = 0. 
No carry to hundreds, Z = 0. 
Check: 04 + 7 = 11 (Z11 = 011, Z = 0, Y = 7).

Q5:  Uneek wants to find all 5-beat rhythms (sums of 1’s and 2’s). The number of ways to write 5 as a sum of 1’s and 2’s is ______. 

Ans: 8
Sol: The number of ways to write n as a sum of 1s and 2s is the nth Virahãnka-Fibonacci number: 
1, 2, 3, 5, 8, ... 
For n = 5, the 5th term is 8. 
List: 
1+1+1+1+1, 
1+1+1+2, 
1+1+2+1, 
1+2+1+1, 
2+1+1+1, 
1+2+2, 
2+1+2, 
2+2+1 (8 ways). 

Q6:  Ishan has number cards with values 1, 3, 5, 7, and 9. She wants to select 3 cards that sum to 21. The number of ways to select 3 cards summing to 21 is _______. 

Ans: 

Ishan selects 3 cards from 1, 3, 5, 7, 9 to sum to 21. List combinations:

Possible sums of 3 odd numbers (all cards are odd): Check combinations systematically.

Try: 9 + 7 + 5 = 21 (works).

Other combinations:

9 + 7 + 3 = 19 (too low).

9 + 7 + 1 = 17.

9 + 5 + 3 = 17.

9 + 5 + 1 = 15.
7 + 5 + 3 = 15.

7 + 5 + 1 = 13.
5 + 3 + 1 = 9.
Only 9 + 7 + 5 = 21 is valid. 
Number of ways to select these 3 cards: 1 combination. 
Verify: No other triplets yield 21, as odd sums must be odd, and 21 is odd, but only this set works. 

Section C: Word Problems

Q7: Priya and Rohan, two siblings born one year apart, celebrate their birthdays. Priya claims the sum of their ages is 25. Is this possible? 

Ans: Since they are born one year apart, their ages are consecutive: n and n+1. 
We need n + (n+1) = 25. 
Solve: 2n + 1 = 25, 
so 2n = 24, n = 12. 
Ages: 12 and 13. 
Sum: 12 + 13 = 25, which is possible. 
Verify: Try other sums (e.g., 24: 2n + 1 = 24, 2n = 23, n = 11.5, not integer). 
Only 25 works for integer ages. 

Q8: Write the next 3 numbers in the sequence: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89. 

Ans: The Virahãnka-Fibonacci sequence has each term as the sum of the two previous terms: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ... Calculate:

11th: 55 + 89 = 144.

12th: 89 + 144 = 233.

13th: 144 + 233 = 377.
The next 3 numbers are 144, 233, 377. The second is 233. Verify: 55 + 89 = 144, 89 + 144 = 233, 144 + 233 = 377.

Q9: Two consecutive numbers in the Virahãnka sequence are 987 and 1597. What are the next 2 numbers in the sequence? Find the second of the next 2 numbers.

Ans: In the Virahãnka-Fibonacci sequence (Fn = Fn-1 + Fn-2):

Given 987 (Fn-1), 1597 (Fn), compute next terms:

Fn+1 = 987 + 1597 = 2584.

Fn+2 = 1597 + 2584 = 4181.
The next 2 numbers are 2584, 4181. The second is 4181. Verify: 610 + 987 = 1597, 987 + 1597 = 2584, 1597 + 2584 = 4181.

Q10: A light bulb is OFF. A student toggles its switch 50 times. How many times is the bulb ON after 50 toggles? [Count ON state, 1 for ON, 0 for OFF.]

Ans: 25
Sol: Each toggle switches the bulb’s state (ON to OFF, OFF to ON). 
Starting ON: 1 toggle → OFF, 2 toggles → ON, etc. 
The state after n toggles is 
ON if n is even, 
OFF if n is odd. 
Here, n = 50 (odd, 50 ÷ 2 = 25 remainder 0). 
The light bulb is ON 25 times after 50 toggles.

Q11: Using the generalized form, find a magic square if the center number is 13. 

Ans: 39
Sol: Odd numbers: 1, 3, 5, 7, ... 
The nth odd number is 2n - 1 : 
n = 1 → 1, 
n = 2 → 3, 
n = 3 → 5. 
For the 20th odd number, n = 20: 2 × 20 - 1 = 40 - 1 = 39. 

Q12: Vanshika wants to climb a 9-step staircase, taking either 1 or 2 steps at a time. In how many different ways can she reach the top?

Ans: 55
Sol: This is a classic Fibonacci-type problem.
Let F(n) be the number of ways to climb n steps using 1 or 2 steps at a time.
Then:

F(n)=F(n−1)+F(n−2)

Because:

• From step (n−1), she can take 1 step

• From step (n−2), she can take 2 steps

Base Cases:

• F(1) = 1 (only one way: 1)

• F(2) = 2 (1+1 or 2)

Compute up to F(9):

There are 55 different ways for Vanshika to climb a 9-step staircase taking 1 or 2 steps at a time.