Decimal Numbers | Mathematics (Maths) Class 7 PDF Download
Multiplying Decimals
Multiplying decimals is very important when we talk about the grouping of items. Suppose you have to distribute 0.25 part of a chocolate bar to each child and there is a total of 12 children. How many chocolate bars would you need? To find the number of chocolate bars required, we have to multiply 12 by 0.25.
Did you know that the history of decimals traces back to the ancient days in countries like China and India? Decimals were even adopted to the counting system by the Egyptians. By around 1500, almost all professional mathematicians accepted decimals and thus they became an integral part of the counting system around the world.
How to Multiply Decimals?
Multiplying Decimals has the same procedure as that of multiplication of the whole numbers, except the placement of the decimal point in the product. In our everyday life, we have come across various instances where we have to use the multiplication operation on two numbers out of which at least one or both are decimal numbers. Imagine going out with your friend for lunch. You both order a platter costing $6.75 each. The total bill amounts to $15.75, including the taxes. To calculate the total cost of the platter in the bill, you need to multiply $6.75 × 2. Similarly, suppose you plan to gift your mother a flower bouquet on her birthday. Each flower costs $0.75 and you buy a total of 6 flowers. To find the total cost of the bouquet, you need to multiply $0.75 × 6. The above examples follow the application of multiplying decimals.
Multiplying Decimals with Whole Numbers
Multiplication of decimals with whole numbers is similar to the multiplication of whole numbers, the only difference being in the placement of the decimal point. The following steps can be followed to multiply decimals with whole numbers:
- Step 1: Initially, Ignore the decimal point and multiply the two numbers normally.
- Step 2: After multiplication, count the number of decimal places in decimal numbers. The product obtained after multiplication will have the same number of decimal places.
- Step 3: Place the decimal point in the obtained product following Step 2.
Let us understand a real-life situation where we multiply decimal numbers. A class of 15 students decided to contribute to a relief fund. Each student made a contribution of $6.5. What was the total amount collected from the whole class? Here, the contribution made by one student = $6.5. Total contribution made by 15 students = 6.5 × 15= $97.5.
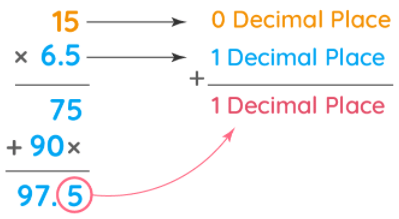 Multiplying of decimals with whole numbers
Multiplying of decimals with whole numbers
Multiplying a decimal by Powers of 10
While multiplying any decimal by 10,100,1000, or any other power of 10, we just simply shift the decimal point towards the right as many places as the number of zeroes in the power of 10
- If we multiply any decimal by 10, we shift the decimal point one place towards the right, as there is 1 zero in the number 10
- If we multiply any decimal by 100, we shift the decimal point two places towards the right.
- Similarly, if we multiply a decimal by 1000, we shift the decimal point by three places towards the right, and so on.
For example, 2.32×10 = 23.2, 2.32×100 = 232, 2.32×1000 = 2320.
Multiplying Two Decimals Numbers
This section will help you to learn about the multiplication of two decimal numbers. It is the same as that of the whole number, but the only difference is that in this we have to take the sum of the total number of decimal places in both the given numbers and that needs to be equal to the number of decimal places in the product. To multiply two decimals, follow the step listed below:
- Step 1: Initially, Ignore the decimal point and multiply the two numbers normally.
- Step 2: After multiplication, count the total number of decimal places in both the numbers combined. The product obtained after multiplication will have this total number of decimal places.
- Step 3: Place the decimal point in the obtained product following Step2.
Let us see the multiplication of two decimal numbers in the image given below:
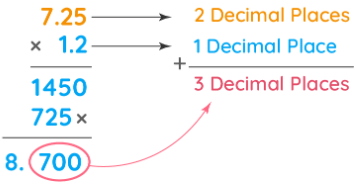 Multiplying Two Decimals Numbers
Multiplying Two Decimals Numbers
Note: Zeros on the extreme right of decimal places can be dropped
→ 8.7
Examples:
1. Multiply 0.567 and 13.065
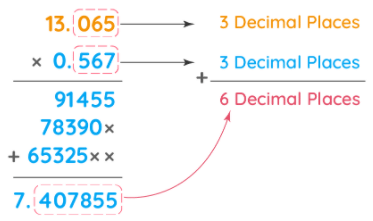
Therefore, 0.567 × 13.065 = 7.407855. There are 6 digits after the decimal point.
2. Find the product of 16.45 and 8.5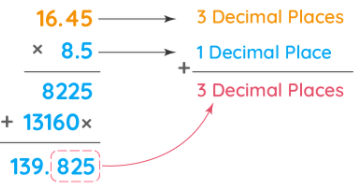
Therefore, 16.45 × 8.5 = 139.825. The product has 3 digits after the decimal point.
Important Notes:
- The decimal multiplication follows the same procedure as the multiplication of whole numbers.
- The decimal point should be placed in the product in such a way that, the product has a number of decimal places equal to the sum of decimal places of all the multiplicands and the multipliers.
- Make sure you keep all the zeros in the product while placing the decimal point.
- If the product has more decimal places than the number of digits, zeros can be inserted before placing the decimal point in the product.
- The trailing zeros in the resultant product can be dropped.
Dividing Decimals
Dividing Decimals is similar to dividing whole numbers, except for the way we handle the decimal point. When we divide decimals, we change the divisor to a whole number by moving the decimal point all the way to the right. Then, we move the decimal point of the dividend up to the same number of places to the right, and divide the resultant numbers in the normal way as we do regular division.
Let us learn more about the division of decimals by reading the content given below, which will help us to understand this better.
What are Decimals?
Decimals are a part of the extended number system to express tenths, hundredths, thousandths, and so on. Working with decimals may seem a bit complex but the various operations using decimal numbers is quite similar to the operations using whole numbers. A decimal number has a whole number part and the fractional part separated by a dot. The digits following the decimal point show a value smaller than one.
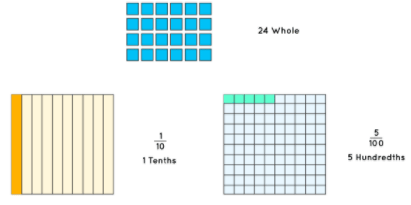 Block Representation - Dividing-decimalsFor example, 24.15 is a decimal number with 24 in its number part and 15 in the decimal part. This can be understood with the following explanation: 24.15= 20 + 4 + 0.1 + 0.05.
Block Representation - Dividing-decimalsFor example, 24.15 is a decimal number with 24 in its number part and 15 in the decimal part. This can be understood with the following explanation: 24.15= 20 + 4 + 0.1 + 0.05.
Dividing Decimals Definition
The process of dividing decimals is similar to the normal division process, but we just need to keep in mind the decimal point which should be correctly placed in the quotient. Since we are referring to decimals, the following steps will help us to understand the process of dividing decimals.
- To divide a decimal number by a whole number, the division is performed in the same way as in the whole numbers. We first divide the two numbers ignoring the decimal point. Then, the decimal point in the quotient is placed in the same position as in the dividend. For example, 18.2 ÷ 2 = 9.1
- To divide a decimal number by a decimal number, multiply the divisor by as many tens as necessary until we get a whole number, and remember to multiply the dividend by the same number of tens. For example, 13.8 ÷ 0.6 becomes 138 ÷ 6 = 23.
Dividing Decimals by Whole Numbers: Dividing decimals by whole numbers is similar to the normal division. Here the dividend is a decimal and the divisor is a whole number, so the quotient will have the number of decimals based on the decimals in the dividend. The division of decimals with a whole number is easily done by taking the following steps.
- Step 1: For example to divide 78.92 ÷ 4, ignore the decimal and divide normally until you get 0 as the remainder.
- Step 2: Place the decimal point in the quotient in the same position as given in the dividend. 78.92 ÷ 4=19.73. Thus, we get 19.73 as the answer, where the decimal is placed according to the decimal of the dividend.
Dividing Decimals by another Decimal Number: In this division, both the dividend and the divisor are decimals and we can solve them by two methods. In the first method, we first move the decimals of the divisor to make it a whole number, and then we move the decimals of the dividend. Let us understand this with the help of the following steps:
- Step 1: For example, to divide 48.5 by 3.5, move the decimal of the divisor to the right as many times as necessary to make it a whole number. This makes the divisor 35.
- Step 2: Move the decimal in the dividend up to the same number of digits as you moved it in the divisor. This makes the divisor 485.
- Step 3: Now, divide the dividend (485) by the divisor (35) just like regular division.
The second method is used when the number of digits after the decimal in the dividend is more or less than the number of decimals in the divisor.
If the dividend's decimal place is more than or equal to the divisor's decimal place:
- Step 1: Ignore the decimal and divide normally until you get 0 as the remainder. For example, to divide: 0.09 ÷ 0.3, we ignore the decimals and write it as 9 ÷ 3 = 3.
- Step 2: Place the decimal point using the formula: Dividend's decimal place - Divisor's decimal place= Quotient's decimal place. Now, using the formula, we get 2-1 = 1. Hence, the decimal of the quotient will be placed as 0.3
If the dividend's decimal place is less than the divisor's decimal place:
In this case, convert the decimal to a fraction. For example: 0.4 ÷ 0.02 = 4/10 ÷ 2/100 = 4/10 × 100/2 = 20
Dividing Decimals Through Long Division
The long division with decimals can be easily done just as the normal long division. The following sequence of steps explain the process of long division of decimals.
- First, write the division in the standard form. Start by dividing the whole number part by the divisor.
- Place the decimal point in the quotient above the decimal point of the dividend. Bring down the tenth digit.
- Divide and bring down the other digit in sequence. Divide until 0 is obtained in the remainder. Thus, the decimal in the quotient is similar is equal to the decimal in the dividend.
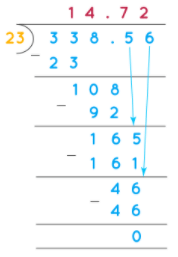 Long-division for Dividing-decimals
Long-division for Dividing-decimals
Now, let us look at the following tips that are helpful while dividing decimals.
- Convert the divisor to a whole number by multiplying by the powers of 10. Multiply the dividend by the same powers of 10.
- When you divide a decimal number by 10, move the decimal point to the left by one place.
- When you divide a decimal number by 100, move the decimal point to the left by two places.
- When you divide a decimal number by 1000, move the decimal point to the left by three places.
|
76 videos|344 docs|39 tests
|
FAQs on Decimal Numbers - Mathematics (Maths) Class 7
| 1. What is the process for multiplying decimals? |  |
| 2. Can you provide an example of multiplying decimals? |  |
| 3. Is there any special rule to remember when multiplying decimals? |  |
| 4. How can we use the concept of multiplying decimals in real-life situations? |  |
| 5. What is the difference between multiplying whole numbers and multiplying decimals? |  |























