Real Numbers Class 10 Notes Maths Chapter 1
| Table of contents |

|
| Real Numbers |

|
| Classification of Real Numbers |

|
| Fundamental Theorem of Arithmetic |

|
| HCF and LCM by Prime Factorisation Method |

|
| Revisiting Irrational Numbers |

|
Real Numbers
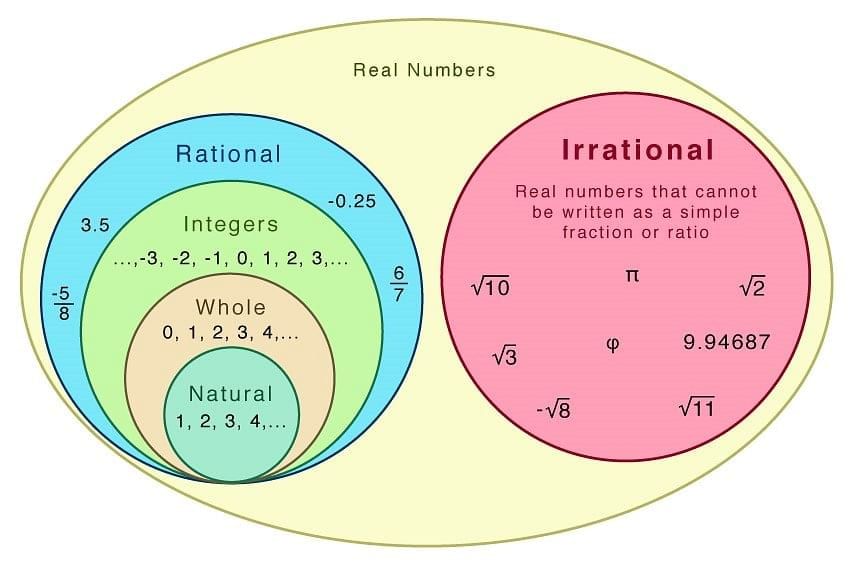
Real numbers are all the numbers that can be found on the number line. This includes both rational numbers (like 7, -3, 0.5, and 4/3) and irrational numbers (like √2) . They encompass integers, fractions, and decimals, representing a continuous, unbroken set of values.
 Rational numbers such as integers (-2, 0, 1), fractions (1/2, 2.5) and irrational numbers such as √3, π(22/7), etc., are all real numbers.
Rational numbers such as integers (-2, 0, 1), fractions (1/2, 2.5) and irrational numbers such as √3, π(22/7), etc., are all real numbers.
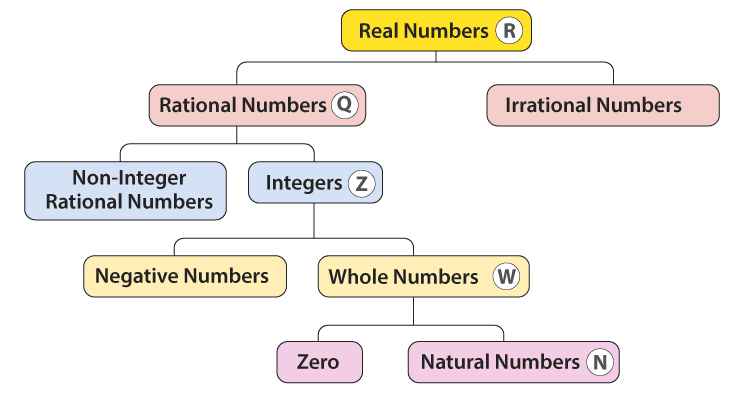
Classification of Real Numbers
- Natural Numbers: Natural Numbers are a set of counting numbers. They are denoted by N.
N = {1, 2, 3, 4..........∞} - Whole Numbers: Whole numbers are a set of natural numbers plus zero.
W = {0, 1, 2, 3 ......... ∞} - Integers: Integers is a set of whole numbers and negative of all natural numbers.
Z = { -3, -2, -1, 0, 1, 2, 3} - Rational Numbers: All the numbers that can be written in the p/q form where p and q are integers and q ≠ 0 are called rational numbers.
E.g. 8/11, -3/17 - Irrational Numbers: All the numbers that cannot be written in the p/q form are called irrational numbers. All the non-terminating and non-repeating decimal numbers are irrational numbers.
E.g. √5, √3, √5 + √3, π
Fundamental Theorem of Arithmetic
To understand the fundamental theorem of Arithmetic, first, it is important to know what are composite numbers and prime numbers.
Composite Number
Composite Numbers are those numbers that have at least one factor other than one and the number itself.
Consider a number, 10. Now, the factors of 10 are 1, 2, 5 and 10. So it is a composite number.
Prime Number
Prime Numbers are those numbers that have exactly two factors: 1 and the number itself.
Let us take one more number 23. Now, the factors of 23 are 1 and 23. That means it has two factors 1 and the number itself, which is called a prime number.
 Prime and Composite Numbers
Prime and Composite Numbers
Theorem: Fundamental Theorem of Arithmetic states that every composite number can be expressed as a product of primes, and this factorization is unique, apart from the order in which the prime factors occur.
Any composite number can be written as a product of primes in one way only as long as we are not particular about the order in which the primes occur.
Let us consider an example here: we will use a tree diagram to show the factors of 270.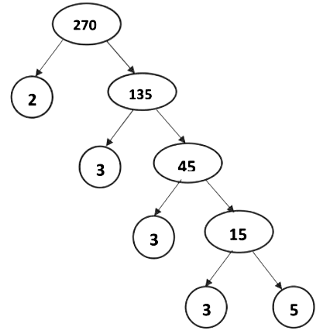 270 = 2 x 33 x 5
270 = 2 x 33 x 5
Here, in the prime factorization of 270, the prime numbers appearing in both cases are the same, only the order in which they appear is different.
Therefore, the prime factorization of 270 is unique except for the order in which the primes occur.
Example 1: Check whether 15n can end with the digit zero for any natural number n.
Sol:

Example 2: Explain, why (7 × 6 × 5 × 4 × 3 × 2 × 1) + 5 and (3 × 5 × 13 × 46) + 23 is a composite number?
Sol:
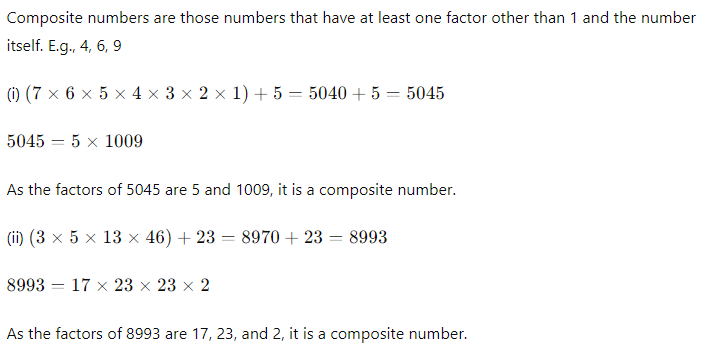
HCF and LCM by Prime Factorisation Method
In this method, we first express the given numbers as a product of prime factors separately. Then, HCF is the product of the smaller power of each common prime factor in the numbers, and LCM is the product of the greatest power of each prime factor involved in the numbers.For any two positive integers a and b,
HCF (a, b) × LCM (a, b) = a × b
Example 3: Find the LCM and HCF of 120 and 144 by the fundamental arithmetic theorem.
Sol:
120 = 23 × 3 × 5
144 = 24 × 32
Now, HCF is the product of the smallest power of each common prime factor in the numbers.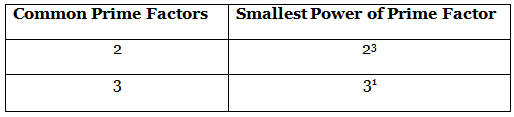 HCF (120, 144) = 23 × 3 = 8 × 3 = 24
HCF (120, 144) = 23 × 3 = 8 × 3 = 24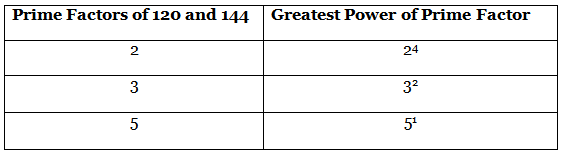 LCM is the product of the greatest power of each prime factor involved in the numbers.
LCM is the product of the greatest power of each prime factor involved in the numbers.
LCM (120,144) = 24 × 32 × 5 = 16 × 9 × 5 = 720
Example 4: If two positive integers p and q can be expressed as p = ab2 and q = a3b, where a, b are prime numbers, find the LCM (p, q).
Sol:
Given: p = ab2 and q = a3b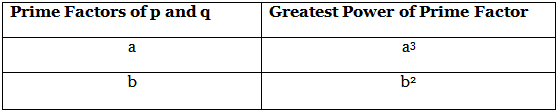 LCM is the product of the greatest power of each prime factor involved in the numbers.
LCM is the product of the greatest power of each prime factor involved in the numbers.
LCM (p, q) = a3 × b2 = a3b2
Example 5: Write the HCF and LCM of the smallest odd composite number and the smallest odd prime number.
Sol:
The smallest odd composite number is 9, and the smallest odd prime number is 3.
9 = 32
3 = 31
Now, the smallest power of the common prime factor is 31.
HCF (9, 3) = 3
The greatest power of the common prime factor is 32.
LCM (9, 3) = 32 = 9
Example 6: If HCF (253,440) = 11 and LCM (253,440)= 253 × R. Find the value of R.
Sol:
We know that,
HCF (a, b) × LCM (a, b) = a × b
∴ HCF (253, 440) × LCM (253, 440) = 253 × 440
11 × 253 × R = 253 × 440
R = 253 x 440 / 253 x 11
R = 40
Example 7: Ravi and Shikha drive around a circular sports field. Ravi takes 16 min to complete one round, while Shikha completes the round in 20 min. If both start at the same point, at the same time, and go in the same direction, then how much time will they meet at the starting point?
Sol:
Time taken by Ravi to drive one round of the circular field = 16 min. Time taken by Shikha to drive one round of the circular field =20 min.
The time after which they will again meet at the starting point will be equal to the LCM of 16 min and 20 min.
16 = 24
20 = 22 × 5
LCM(16, 20) = 24 × 5 = 16 × 5 = 80
Therefore, Ravi and Shikha will meet again at the starting point after 80 min.
Revisiting Irrational Numbers
Irrational numbers are those numbers that cannot be written in the form p/q, where p and q are integers and q ≠0. E.g.,√2, √3, √15
The square roots of all the numbers do not give an irrational number.
 For example, √2 is an irrational number, but √4 = 2, which is rational.
For example, √2 is an irrational number, but √4 = 2, which is rational.
Therefore, the square roots of all prime numbers are irrational.
If p is a prime number, then √p is an irrational number.
Theorem : If a prime number p divides a2, then p divides a, where a is a positive integer.

Theorem: Prove that √2 is an irrational number.
Sol:

Example 8: Show that 3√2 is an irrational number.
Sol:

Example 9: Show that 5 − √3 is irrational.
Sol:

|
127 videos|584 docs|79 tests
|
FAQs on Real Numbers Class 10 Notes Maths Chapter 1
| 1. What are the different classifications of real numbers? |  |
| 2. What is the Fundamental Theorem of Arithmetic? |  |
| 3. How can we find the HCF and LCM using the Prime Factorisation Method? |  |
| 4. Can you explain irrational numbers with examples? |  |
| 5. Why is understanding real numbers important in mathematics? |  |
















