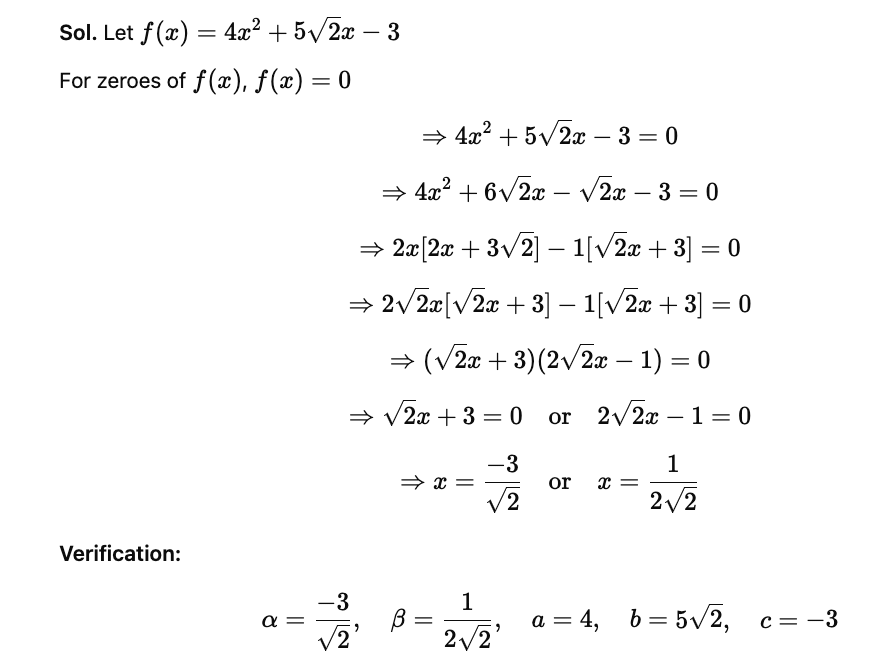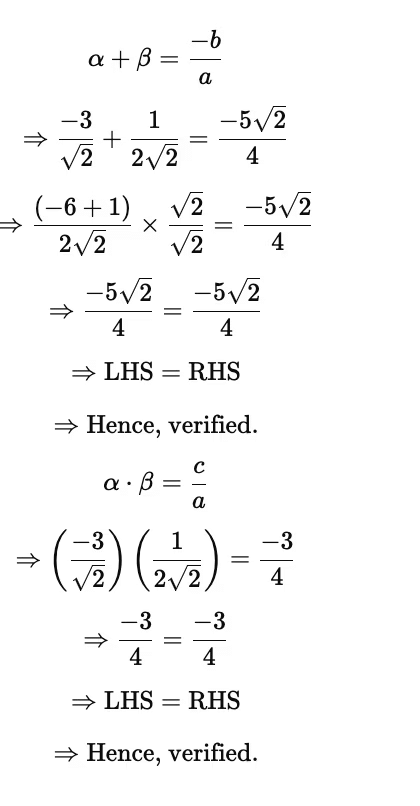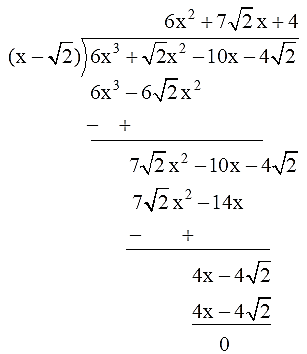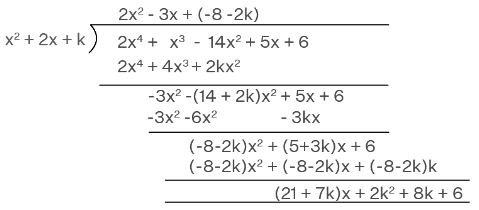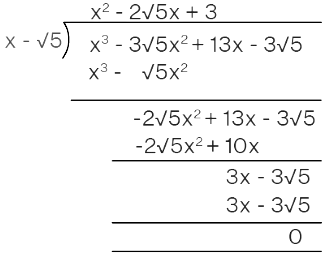NCERT Exemplar: Polynomials - 2 | Mathematics (Maths) Class 10 PDF Download
Exercise 2.3
Find the zeroes of the following polynomials by factorisation method.
Q.1. 4x2 – 3x – 1
4x2 – 3x – 1
Splitting the middle term, we get,
4x2- 4x + 1x - 1
Taking the common factors out, we get,
4x(x - 1) +1(x - 1)
On grouping, we get,
(4x + 1)(x - 1)
So, the zeroes are,
4x + 1 = 0⇒ 4x = -1 ⇒x = (-1/4)
(x-1) = 0 ⇒ x = 1
Therefore, zeroes are (-1/4) and 1
Verification:
Sum of the zeroes = – (coefficient of x) ÷ coefficient of x2
α + β = – b/a
1 – 1/4 = – (- 3)/4 = ¾
Product of the zeroes = constant term ÷ coefficient of x2
α β = c/a
1(- 1/4) = – ¼
– 1/4 = – 1/4
Q.2. 3x2 + 4x – 4
3x2 + 4x – 4
Splitting the middle term, we get,
3x2 + 6x – 2x – 4
Taking the common factors out, we get,
3x(x + 2) -2(x + 2)
On grouping, we get,
(x + 2)(3x - 2)
So, the zeroes are,
x + 2 =0 ⇒ x = -2
3x - 2 = 0 ⇒ 3x = 2 ⇒ x = 2/3
Therefore, zeroes are (2/3) and -2
Verification:
Sum of the zeroes = – (coefficient of x) ÷ coefficient of x2
α + β = – b/a
– 2 + (2/3) = – (4)/3
= – 4/3 = – 4/3
Product of the zeroes = constant term ÷ coefficient of x2
α β = c/a
Product of the zeroes = (- 2) (2/3) = – 4/3
Q.3. 5t2 + 12t + 7
5t2 + 12t + 7
Splitting the middle term, we get,
5t2 + 5t + 7t + 7
Taking the common factors out, we get,
5t (t + 1) +7(t + 1)
On grouping, we get,
(t + 1)(5t + 7)
So, the zeroes are,
t + 1 = 0 ⇒ y = -1
5t+7=0 ⇒ 5t=-7⇒t=-7/5
Therefore, zeroes are (-7/5) and -1
Verification:
Sum of the zeroes = – (coefficient of x) ÷ coefficient of x2
α + β = – b/a
(- 1) + (- 7/5) = – (12)/5
= – 12/5 = – 12/5
Product of the zeroes = constant term ÷ coefficient of x2
α β = c/a
(- 1)(- 7/5) = 7/5
7/5 = 7/5
Q.4. t3 – 2t2 – 15t
t3 – 2t2 – 15t
Taking t common, we get,
t ( t2 -2t -15)
Splitting the middle term of the equation t2 -2t -15, we get,
t( t2 -5t + 3t -15)
Taking the common factors out, we get,
t (t (t-5) +3(t-5)
On grouping, we get,
t (t+3)(t-5)
So, the zeroes are,
t=0
t+3=0 ⇒ t= -3
t -5=0 ⇒ t=5
Therefore, zeroes are 0, 5 and -3
Verification:
Sum of the zeroes = – (coefficient of x2) ÷ coefficient of x3
α + β + γ = – b/a
(0) + (- 3) + (5) = – (- 2)/1
= 2 = 2
Sum of the products of two zeroes at a time = coefficient of x ÷ coefficient of x3
αβ + βγ + αγ = c/a
(0)(- 3) + (- 3) (5) + (0) (5) = – 15/1
= – 15 = – 15
Product of all the zeroes = – (constant term) ÷ coefficient of x3
αβγ = – d/a
(0)(- 3)(5) = 0
Q.5. 2x2 +(7/2)x +3/4
2x2 +(7/2)x +3/4
The equation can also be written as,
8x2+14x+3
Splitting the middle term, we get,
8x2+12x+2x+3
Taking the common factors out, we get,
4x (2x+3) +1(2x+3)
On grouping, we get,
(4x+1)(2x+3)
So, the zeroes are,
4x+1=0 ⇒ x = -1/4
2x+3=0 ⇒ x = -3/2
Therefore, zeroes are -1/4 and -3/2
Verification:
Sum of the zeroes = – (coefficient of x) ÷ coefficient of x2
α + β = – b/a
(- 3/2) + (- 1/4) = – (7)/4
= – 7/4 = – 7/4
Product of the zeroes = constant term ÷ coefficient of x2
α β = c/a
(- 3/2)(- 1/4) = (3/4)/2
3/8 = 3/8
Q.6. .
Hence, verified.\Rightarrow \text{Hence, verified.}
Q.7. 2s2 - (1 + 2√2)s + √2
Given, the polynomial is 2s² - (1+ 2√2)s + √2.
We have to find the relation between the coefficients and zeros of the polynomial
Let 2s² - (1+ 2√2)s + √2 = 0
On factoring,
2s² - s - 2√2s + √2 = 0
2s² - 2√2s - s + √2 = 0
2s(s - √2 ) - 1(s - √2) = 0
(2s - 1)(s - √2) = 0
Now, 2s - 1 = 0
2s = 1
s = 1/2
Also, s - √2 = 0
s = √2
Therefore, the zeros of the polynomial are 1/2 and √2.
Q.8. v2 + 4√3v - 15
Given, the polynomial is v² + 4√3v - 15.
We have to find the relation between the coefficients and zeros of the polynomial
Let v² + 4√3v - 15 = 0
On factoring,
v² + 5√3v - √3v - 15 = 0
v(v + 5√3) - √3(v + 5√3) = 0
(v - √3)(v + 5√3) = 0
Now, v - √3 = 0
v = √3
Also, v + 5√3 = 0
v = -5√3
Therefore, the zeros of the polynomial are -5√3 and √3.
We know that, if α and β are the zeroes of a polynomial ax² + bx + c, then
Sum of the roots is α + β = -coefficient of x/coefficient of x² = -b/a
Product of the roots is αβ = constant term/coefficient of x² = c/a
From the given polynomial,
coefficient of x = 4√3
Coefficient of x² = 1
Constant term = -15
Sum of the roots:
LHS: α + β
= √3 - 5√3
= -4√3
RHS: -coefficient of x/coefficient of x²
= -4√3/1
= -4√3
LHS = RHS
Product of the roots
LHS: αβ
= (-5√3)(√3)
= -15
RHS: constant term/coefficient of x²
= -15/1
= -15
LHS = RHS
Q.9. 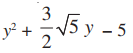
Given, the polynomial is y² + (3√5/2)y - 5.
We have to find the relation between the coefficients and zeros of the polynomial
The polynomial can be rewritten as (1/2)[2y² + 3√5y - 10].
Let 2y² + 3√5y - 10 = 0
On factoring,
2y² + 4√5y - √5y - 10 = 0
2y(y + 2√5) - √5(y - 2√5) = 0
(y + 2√5)(2y - √5) = 0
Now, y + 2√5 = 0
y = -2√5
Also, 2y - √5 = 0
2y = √5
x = √5/2
Therefore, the zeros of the polynomial are √5/2 and -2√5.
We know that, if α and β are the zeroes of a polynomial ax² + bx + c, then
Sum of the roots is α + β = -coefficient of x/coefficient of x² = -b/a
Product of the roots is αβ = constant term/coefficient of x² = c/a
From the given polynomial,
coefficient of x = 3√5
Coefficient of x² = 2
Constant term = -10
Sum of the roots:
LHS: α + β
= √5/2 - 2√5
= (√5 - 4√5)/2
= -3√5/2
RHS: -coefficient of x/coefficient of x²
= -3√5/2
LHS = RHS
Product of the roots
LHS: αβ
= (√5/2)(-2√5)
= -10/2
= -5
RHS: constant term/coefficient of x²
= -10/2
= -5
LHS = RHS
Q.10. 7y2-11/3y - 2/3
Given, the polynomial is 7y² - (11/3)y - (2/3).
We have to find the relation between the coefficients and zeros of the polynomial
The polynomial can be rewritten as (1/3)[21y² - 11y - 2]
Let (1/3)[21y² - 11y - 2] = 0
21y² - 11y - 2 = 0
On factoring,
21y² - 14y + 3y - 2 = 0
7y(3y - 2) + (3y - 2) = 0
(7y + 1)(3y - 2) = 0
Now, 7y + 1 = 0
7y = -1
y = -1/7
Also, 3y - 2 = 0
3y = 2
y = 2/3
Therefore, the zeros of the polynomial are 2/3 and -1/7.
We know that, if α and β are the zeroes of a polynomial ax² + bx + c, then
Sum of the roots is α + β = -coefficient of x/coefficient of x² = -b/a
Product of the roots is αβ = constant term/coefficient of x² = c/a
From the given polynomial,
coefficient of x = -11
Coefficient of x² = 21
Constant term = -2
Sum of the roots:
LHS: α + β
= -1/7 + 2/3
= (-3+14)/21
= 11/21
RHS: -coefficient of x/coefficient of x²
= -(-11)/21
= 11/21
LHS = RHS
Product of the roots
LHS: αβ
= (-1/7)(2/3)
= -2/21
RHS: constant term/coefficient of x²
= -2/21
LHS = RHS
Exercise 2.4
Q.1. For each of the following, find a quadratic polynomial whose sum and product respectively of the zeroes are as given. Also find the zeroes of these polynomials by factorisation.
(i) (–8/3), 4/3
(ii) 21/8, 5/16
(iii) -2√3, -9
(iv) (-3/(2√5)), -1/2
(i) Sum of the zeroes = – 8/3
Product of the zeroes = 4/3
P(x) = x2 – (sum of the zeroes) + (product of the zeroes)
Then, P(x)= x2 – (-8x)/3 + 4/3
P(x)= 3x2 + 8x + 4
Using splitting the middle term method,
3x2 + 8x + 4 = 0
3x2 + (6x + 2x) + 4 = 0
3x2 + 6x + 2x + 4 = 0
3x(x + 2) + 2(x + 2) = 0
(x + 2)(3x + 2) = 0
⇒ x = -2, -2/3
(ii) Sum of the zeroes = 21/8
Product of the zeroes = 5/16
P(x) = x2 – (sum of the zeroes) + (product of the zeroes)
Then, P(x)= x2 – 21x/8 + 5/16
P(x)= 16x2 – 42x + 5
Using splitting the middle term method,
16x2 – 42x + 5 = 0
16x2 – (2x + 40x) + 5 = 0
16x2 – 2x – 40x + 5 = 0
2x (8x – 1) – 5(8x – 1) = 0
(8x – 1)(2x – 5) = 0
⇒ x = 1/8, 5/2
(iii) Sum of the zeroes = – 2√3
Product of the zeroes = – 9
P(x) = x2 – (sum of the zeroes) + (product of the zeroes)
Then, P(x) = x2 – (-2√3x) – 9
Using splitting the middle term method,
x2 + 2√3x – 9 = 0
x2 + (3√3x – √3x) – 9 = 0
x(x + 3√3) – √3(x + 3√3) = 0
(x – √3)(x + 3√3) = 0
⇒ x = √3, -3√3
(iv) Sum of the zeroes = -3/2√5x
Product of the zeroes = – ½
P(x) = x2 – (sum of the zeroes) + (product of the zeroes)
Then, P(x)= x2 -(-3/2√5x) – ½
P(x)= 2√5x2 + 3x – √5
Using splitting the middle term method,
2√5x2 + 3x – √5 = 0
2√5x2 + (5x – 2x) – √5 = 0
2√5x2 – 5x + 2x – √5 = 0
√5x (2x + √5) – (2x + √5) = 0
(2x + √5)(√5x – 1) = 0
⇒ x = 1/√5, -√5/2
Q.2. Given that the zeroes of the cubic polynomial x3 – 6x2 + 3x + 10 are of the form a, a + b, a + 2b for some real numbers a and b, find the values of a and b as well as the zeroes of the given polynomial.
Given that a, a + b, a + 2b are roots of given polynomial x³ - 6x² + 3x + 10
Sum of the roots ⇒ a + 2b + a + a + b = -coefficient of x²/ coefficient of x³
⇒ 3a+3b = -(-6)/1 = 6
⇒ 3(a+b) = 6
⇒ a+b = 2 ........(1)b = 2-a
Product of roots ⇒ (a+2b)(a+b)a = -constant/coefficient of x³
⇒ (a+b+b)(a+b)a = -10/1
Substituting the value of a+b=2 in it
⇒ (2+b)(2)a = -10
⇒ (2+b)2a = -10
⇒ (2+2-a)2a = -10
⇒ (4-a)2a = -10
⇒ 4a-a² = -5
⇒ a²-4a-5 = 0
⇒ a²-5a+a-5 = 0
⇒ (a-5)(a+1) = 0
a-5 = 0 or a+1 = 0
a = 5 a = -1
a = 5, -1 in (1) a+b = 2
When a = 5, 5+b=2 ⇒ b=-3
a = -1, -1+b=2 ⇒ b= 3
∴ If a=5 then b= -3
or
If a= -1 then b=3
Q.3. Given that √2 is a zero of the cubic polynomial 6x3 + √2 x2 – 10x – 4√2 , find its other two zeroes.
Given, √2 is one of the zero of the cubic polynomial.
Then, (x-√2) is one of the factor of the given polynomial p(x) = 6x³+√2x²-10x- 4√2.
So, by dividing p(x) by x-√2
6x³+√2x²-10x-4√2= (x-√2) (6x² +7√2x + 4)
By splitting the middle term,
We get,
(x-√2) (6x² + 4√2x + 3√2x + 4)
= (x-√2) [2x(3x+2√2) + √2(3x+2√2)]
= (x-√2) (2x+√2) (3x+2√2)
To get the zeroes of p(x),
Substitute p(x)= 0
(x-√2) (2x+√2) (3x+2√2)= 0
x= √2, x= -√2/2, x= -2√2/3
Hence, the other two zeroes of p(x) are -√2/2 and -2√2/3
Q.4. Find k so that x2 + 2x + k is a factor of 2x4 + x3 – 14x2 + 5x + 6. Also find all the zeroes of the two polynomials.
Given, p(x) = 2x⁴ + x³ - 14 x² + 5x + 6.
g(x) = x² + 2x + k
We have to find the zeros of the polynomial.
The division algorithm states that given any polynomial p(x) and any non-zero
polynomial g(x), there are polynomials q(x) and r(x) such that
p(x) = g(x) q(x) + r(x), where r(x) = 0 or degree r(x) < degree g(x).
Let r(x) = 0
So, p(x) = g(x) q(x)
By using long division,
So, q(x) = 2x² - 3x - 8 - 2k
r(x) = (21+7k)x + (2k² + 8k + 6)
By comparing the coefficients of (21+7k)x and 2k² + 8k + 6
2k² + 8k + 6 = 0
2(k² + 4k + 3) = 0
k² + 3k + k + 3 = 0
k(k + 3) + (k + 3) = 0
(k + 1)(k + 3) = 0
Now, k + 1 = 0
k = -1
Also, k + 3 = 0
k = -3
So, k = -1, -3.
When k = -1,
21 + 7k = 0
= 21 + 7(-1)
= 21 - 7
= 14
21 + 7k is not equal to zero.
So, k = -1 is neglected.
When k = -3,
21 + 7k = 0
= 21 + 7(-3)
= 21 - 21
= 0
Therefore, the value of k is -3.
Now, g(x) = x² + 2x - 3
x² + 2x - 3 = 0
x² - x + 3x - 3 = 0
x(x - 1) + 3(x - 1) = 0
(x + 3)(x - 1) = 0
Now, x + 3 = 0
x = -3
Also, x - 1 = 0
x = 1
Now, q(x) = 2x² - 3x - 8 - 2k
= 2x² - 3x - 8 - 2(-3)
= 2x² - 3x - 8 + 6
= 2x² - 3x - 2
On factoring,
2x² - 3x - 2 = 0
2x² - 4x + x - 2 = 0
2x(x - 2) + (x - 2) = 0
(2x + 1)(x - 2) = 0
Now, 2x + 1 = 0
2x = -1
x = -1/2
Also, x - 2 = 0
x = 2
We know that g(x) and q(x) are the factors of p(x).
So, the zeros of g(x) and q(x) will be the zeros of p(x).
Therefore, the zeros of p(x) = -3, -1/2, 1 and 2.
Q.5. Given that x – √5 is a factor of the cubic polynomial x3 – 3√5x2 + 13x – 3√5, find all the zeroes of the polynomial.
Give, the cubic polynomial p(x) = x³ - 3√5x² + 13x - 3√5
g(x) = x - √5
We have to find all the zeros of the polynomial.
By using long division,
The quotient is g(x) = x² - 2√5x + 3
On factoring,
x² - 2√5x + 3 = 0
Using the quadratic formula,
x= [-b ± √b² - 4ac]/2a
Here, a = 1, b = -2√5 and c = 3
x = [2√5 ± √(-2√5)² - 4 (1) (3)]/ 2(1)
x = [2√5 ± √20 - 12]/ 2
x = [2√5 ± √8]/ 2
x = [2√5 ± 2√2]/ 2
Taking out common terms,
x = 2[√5 ± √2]/ 2
x = √5 ± √2
Therefore, the zeros are √5, √5 ± √2.
|
127 videos|584 docs|79 tests
|
FAQs on NCERT Exemplar: Polynomials - 2 - Mathematics (Maths) Class 10
| 1. What is a polynomial? |  |
| 2. How do you classify polynomials based on the number of terms? |  |
| 3. How do you find the degree of a polynomial? |  |
| 4. What are the different operations that can be performed on polynomials? |  |
| 5. Can a polynomial have a negative degree? |  |