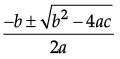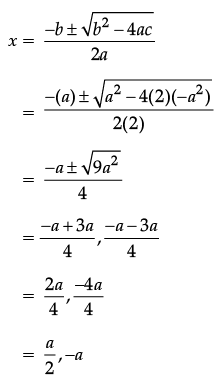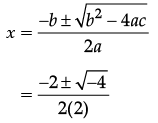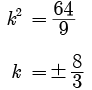All Courses
Get the App Signup / Login
Sign in Open App
Class 10 Exam  >  Class 10 Notes  >  Mathematics (Maths) Class 10  >  Assertion & Reason Type Questions: Quadratic Equations

Class 10 Maths Chapter 4 Assertion and Reason Questions - Quadratic Equations

Q1:

Question for Assertion & Reason Type Questions: Quadratic Equations
Try yourself:Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.

Assertion (A): The degree of quadratic equation is always 2. Hence, x2 – 1 = 0 is pure quadratic equation.

Reason (R): An equation of the form ax2 + c = 0 is known as pure quadratic equation.

View Solution

Q2:

Question for Assertion & Reason Type Questions: Quadratic Equations
Try yourself: Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.

Assertion (A): The product of two successive positive integral multiples of 5 is 300, then the two numbers are 15 and 20.

Reason (R): The product of two consecutive integrals is a multiple of 2.

View Solution

Q3:

Question for Assertion & Reason Type Questions: Quadratic Equations
Try yourself: Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.

Assertion (A): In the expression:Class 10 Maths Chapter 4 Assertion and Reason Questions - Quadratic Equations x can’t have values 3 and – 5

Reason (R): If discriminant D = b2 – 4ac > 0 then the roots of the quadratic equation ax2 + bx + c = 0 are real and unequal.

View Solution

Q4:

Question for Assertion & Reason Type Questions: Quadratic Equations
Try yourself: Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.

Assertion (A): The equation 8x2 + 3kx + 2 = 0 has equal roots than the value of k is ± Class 10 Maths Chapter 4 Assertion and Reason Questions - Quadratic Equations

Reason (R): The equation ax2 + bx + c = 0 has equal roots if D = b2 – 4ac = 0.

View Solution

Q5:

Question for Assertion & Reason Type Questions: Quadratic Equations
Try yourself: Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.

Assertion (A): Values of x are Class 10 Maths Chapter 4 Assertion and Reason Questions - Quadratic Equations a for a quadratic equation 2x2 + ax – a2 = 0.

Reason (R): For quadratic equation ax2 + ax + c = 0, Class 10 Maths Chapter 4 Assertion and Reason Questions - Quadratic Equations

View Solution

Q6:

Question for Assertion & Reason Type Questions: Quadratic Equations
Try yourself: Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.

Assertion (A): Sum of ages of two friends is 20 years. Four years ago, the product of their ages in years was 48. Then the difference between their ages is 16.

Reason (R): For quadratic equation ax2 + bx + c = 0,

Class 10 Maths Chapter 4 Assertion and Reason Questions - Quadratic Equations

View Solution

Q7:

Question for Assertion & Reason Type Questions: Quadratic Equations
Try yourself: Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.

Assertion (A): The roots of the quadratic equation x2 + 2x + 2 = 0 are imaginary.

Reason (B): If discriminant D = b2 – 4ac < 0="" then="" the="" roots="" of="" the="" quadratic="" equation="" />2 + bx + c = 0 are imaginary.

View Solution

Q8:

Question for Assertion & Reason Type Questions: Quadratic Equations
Try yourself: Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.

Assertion (A): If we solve the equation of the form 9(x+2) – 6.(3)(x+1) + 1 = 0, then x = – 2.

Reason (R): The equation of the form x2a + xb + b = 0 can’t be solved by quadratic formula.

View Solution

Q9:

Question for Assertion & Reason Type Questions: Quadratic Equations
Try yourself: Directions: In the following questions, A statement of Assertion (A) is followed by a statement of Reason (R). Mark the correct choice as.

Assertion (A): The equationClass 10 Maths Chapter 4 Assertion and Reason Questions - Quadratic Equations has no root.

Reason (R): x - 1 ≠ 0, then only above equation is defined.

View Solution

Q10:

Question for Assertion & Reason Type Questions: Quadratic Equations
Try yourself: DIRECTION : In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:

Assertion : The equation x2 + 3x+1 = (x - 2)2 is a quadratic equation.

Reason : Any equation of the form ax2 + bx + c = 0 where a ≠ 0 , is called a quadratic equation.

View Solution

Q11:

Question for Assertion & Reason Type Questions: Quadratic Equations
Try yourself: DIRECTION : In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:

Assertion : The values of x are Class 10 Maths Chapter 4 Assertion and Reason Questions - Quadratic Equations a for a quadratic equation 2x2 +ax- a2 =0 .

Reason : For quadratic equation ax2 + bx+ c = 0

Class 10 Maths Chapter 4 Assertion and Reason Questions - Quadratic Equations

View Solution

Q12:

Question for Assertion & Reason Type Questions: Quadratic Equations
Try yourself: DIRECTION : In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:

Assertion : The value of k = 2 , if one root of the quadratic equation 6x2 -x- k = 0 is ⅔

Reason : The quadratic equation ax2 + bx + c = 0, a ≠ 0 a has two roots.

View Solution

Q13:

Question for Assertion & Reason Type Questions: Quadratic Equations
Try yourself:DIRECTION : In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:

Assertion : If roots of the equation x2 - bx + c = 0 are two consecutive integers, then b2 - 4c =1

Reason : If a, b, c are odd integer then the roots of the equation 4abc x2 + (b2 - 4ac)x - b = 0 are real and distinct.

View Solution

Q14:

Question for Assertion & Reason Type Questions: Quadratic Equations
Try yourself: DIRECTION : In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:

Assertion : A quadratic equation ax2 + bx + c = 0 , has two distinct real roots, if b2 - 4ac >0 .

Reason : A quadratic equation can never be solved by using method of completing the squares.

View Solution

Q15:

Question for Assertion & Reason Type Questions: Quadratic Equations
Try yourself: DIRECTION : In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:

Assertion : 4x2 -12x+9 =0 has repeated roots.

Reason : The quadratic equation ax2 + bx + c = 0 have repeated roots if discriminant D > 0 .

View Solution

Q16:

Question for Assertion & Reason Type Questions: Quadratic Equations
Try yourself: DIRECTION : In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:

Assertion : (2x - l)2 - 4x2 + 5 = 0 is not a quadratic equation.

Reason : x = 0, 3 are the roots of the equation 2x2 -60x = 0.

View Solution

Q17:

Question for Assertion & Reason Type Questions: Quadratic Equations
Try yourself: DIRECTION : In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:

Assertion : The equation 8x2 + 23kx+0 = has equal roots then the value of k is Class 10 Maths Chapter 4 Assertion and Reason Questions - Quadratic Equations

Reason : The equation ax2 + bx+ c = 0 has equal roots if D =b2 - 4ac =0

View Solution

Q18:

Question for Assertion & Reason Type Questions: Quadratic Equations
Try yourself: DIRECTION : In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:

Assertion : The roots of the quadratic equation x2 + 2x+2 = 0 are imaginary.

Reason : If discriminant D =b2 - 4ac <0 then="" the="" roots="" of="" quadratic="" equation="">2 + bx+ c = 0 are imaginary.

View Solution

Q19:

Question for Assertion & Reason Type Questions: Quadratic Equations
Try yourself: DIRECTION : In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:

Assertion : The equation 9x2 + 34kx + 4 = 0 has equal roots for k = + 4 .

Reason : If discriminant ‘D’ of a quadratic equation is equal to zero then the roots of equation are real and equal.

View Solution

Q20:

Question for Assertion & Reason Type Questions: Quadratic Equations
Try yourself: DIRECTION : In the following questions, a statement of assertion (A) is followed by a statement of reason (R). Mark the correct choice as:

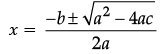
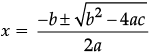
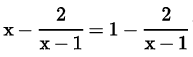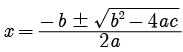
Assertion : Sum and product of roots of 2x2 -35x+0 = are Class 10 Maths Chapter 4 Assertion and Reason Questions - Quadratic Equations andClass 10 Maths Chapter 4 Assertion and Reason Questions - Quadratic Equations respectively.

Reason : If a and b are the roots of ax2 + bx + c = 0 , a ≠ 0 , then sum of roots = α +β = Class 10 Maths Chapter 4 Assertion and Reason Questions - Quadratic Equations and product of roots Class 10 Maths Chapter 4 Assertion and Reason Questions - Quadratic Equations

View Solution

The document Class 10 Maths Chapter 4 Assertion and Reason Questions - Quadratic Equations is a part of the Class 10 Course Mathematics (Maths) Class 10.
All you need of Class 10 at this link: Class 10
126 videos|457 docs|75 tests
Join Course for Free

Top Courses for Class 10

Related Exams
About this Document
4.67/5 Rating
Dec 23, 2024 Last updated
Document Description: Assertion & Reason Type Questions: Quadratic Equations for Class 10 2024 is part of Mathematics (Maths) Class 10 preparation. The notes and questions for Assertion & Reason Type Questions: Quadratic Equations have been prepared according to the Class 10 exam syllabus. Information about Assertion & Reason Type Questions: Quadratic Equations covers topics like and Assertion & Reason Type Questions: Quadratic Equations Example, for Class 10 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Assertion & Reason Type Questions: Quadratic Equations.
Introduction of Assertion & Reason Type Questions: Quadratic Equations in English is available as part of our Mathematics (Maths) Class 10 for Class 10 & Assertion & Reason Type Questions: Quadratic Equations in Hindi for Mathematics (Maths) Class 10 course. Download more important topics related with notes, lectures and mock test series for Class 10 Exam by signing up for free. Class 10: Class 10 Maths Chapter 4 Assertion and Reason Questions - Quadratic Equations
Description
Full syllabus notes, lecture & questions for Class 10 Maths Chapter 4 Assertion and Reason Questions - Quadratic Equations - Class 10 | Plus excerises question with solution to help you revise complete syllabus for Mathematics (Maths) Class 10 | Best notes, free PDF download
Information about Assertion & Reason Type Questions: Quadratic Equations
In this doc you can find the meaning of Assertion & Reason Type Questions: Quadratic Equations defined & explained in the simplest way possible. Besides explaining types of Assertion & Reason Type Questions: Quadratic Equations theory, EduRev gives you an ample number of questions to practice Assertion & Reason Type Questions: Quadratic Equations tests, examples and also practice Class 10 tests
126 videos|457 docs|75 tests
Join Course for Free
Download as PDF
Explore Courses for Class 10 exam

Top Courses for Class 10

Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
10M+ students study on EduRev
Related Searches

Summary

,

video lectures

,

MCQs

,

Class 10 Maths Chapter 4 Assertion and Reason Questions - Quadratic Equations

,

Exam

,

Viva Questions

,

pdf

,

Extra Questions

,

past year papers

,

Semester Notes

,

Previous Year Questions with Solutions

,

mock tests for examination

,

Class 10 Maths Chapter 4 Assertion and Reason Questions - Quadratic Equations

,

Objective type Questions

,

ppt

,

study material

,

Class 10 Maths Chapter 4 Assertion and Reason Questions - Quadratic Equations

,

Free

,

Important questions

,

shortcuts and tricks

,

practice quizzes

,

Sample Paper

;
Additional Information about Assertion & Reason Type Questions: Quadratic Equations for Class 10 Preparation

Assertion & Reason Type Questions: Quadratic Equations Free PDF Download

The Assertion & Reason Type Questions: Quadratic Equations is an invaluable resource that delves deep into the core of the Class 10 exam. These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective. With the help of these notes, you can grasp complex subjects quickly, revise important points easily, and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner, allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material, or toppers' notes, this PDF has got you covered. Download the Assertion & Reason Type Questions: Quadratic Equations now and kickstart your journey towards success in the Class 10 exam.

Importance of Assertion & Reason Type Questions: Quadratic Equations

The importance of Assertion & Reason Type Questions: Quadratic Equations cannot be overstated, especially for Class 10 aspirants. This document holds the key to success in the Class 10 exam. It offers a detailed understanding of the concept, providing invaluable insights into the topic. By knowing the concepts well in advance, students can plan their preparation effectively. Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.

Assertion & Reason Type Questions: Quadratic Equations Notes

Assertion & Reason Type Questions: Quadratic Equations Notes offer in-depth insights into the specific topic to help you master it with ease. This comprehensive document covers all aspects related to Assertion & Reason Type Questions: Quadratic Equations. It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation. Practice papers and question papers enable you to assess your progress effectively. Additionally, the paper analysis provides valuable tips for tackling the exam strategically. Access to Toppers' notes gives you an edge in understanding complex concepts. Whether you're a beginner or aiming for advanced proficiency, Assertion & Reason Type Questions: Quadratic Equations Notes on EduRev are your ultimate resource for success.

Assertion & Reason Type Questions: Quadratic Equations Class 10

The "Assertion & Reason Type Questions: Quadratic Equations Class 10 Questions" guide is a valuable resource for all aspiring students preparing for the Class 10 exam. It focuses on providing a wide range of practice questions to help students gauge their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation. The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level. Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.

Study Assertion & Reason Type Questions: Quadratic Equations on the App

Students of Class 10 can study Assertion & Reason Type Questions: Quadratic Equations alongwith tests & analysis from the EduRev app, which will help them while preparing for their exam. Apart from the Assertion & Reason Type Questions: Quadratic Equations, students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc. The EduRev App will make your learning easier as you can access it from anywhere you want. The content of Assertion & Reason Type Questions: Quadratic Equations is prepared as per the latest Class 10 syllabus.
© EduRev
Education Revolution
Signup to see your scores go up
within 7 days!
Takes less than 10 seconds to signup