Perimeter and Area Class 7 Notes Maths Chapter 9
| Table of contents |

|
| What is Perimeter and Area? |

|
| Area of Parallelograms |

|
| Area of Triangle |

|
| Circles |

|
| Circumference of Circle |

|
What is Perimeter and Area?
Area and perimeter are two fundamental concepts in geometry that describe the size and shape of a 2D object.
Perimeter
- The perimeter of a shape is the total length of its boundary.
- It is calculated by adding the lengths of all sides of the shape.
- Perimeter is measured in linear units such as meters (m), centimeters (cm), or inches (in).

Area
- The area of a shape is the space enclosed within its boundary.
- It is measured in square units such as square meters (m²), square centimeters (cm²), or square inches (in²).

Area of Parallelograms
A parallelogram is a two-dimensional geometrical shape whose sides are parallel to each other. It is a type of polygon having four sides (also called quadrilateral), where the pair of parallel sides are equal in length.
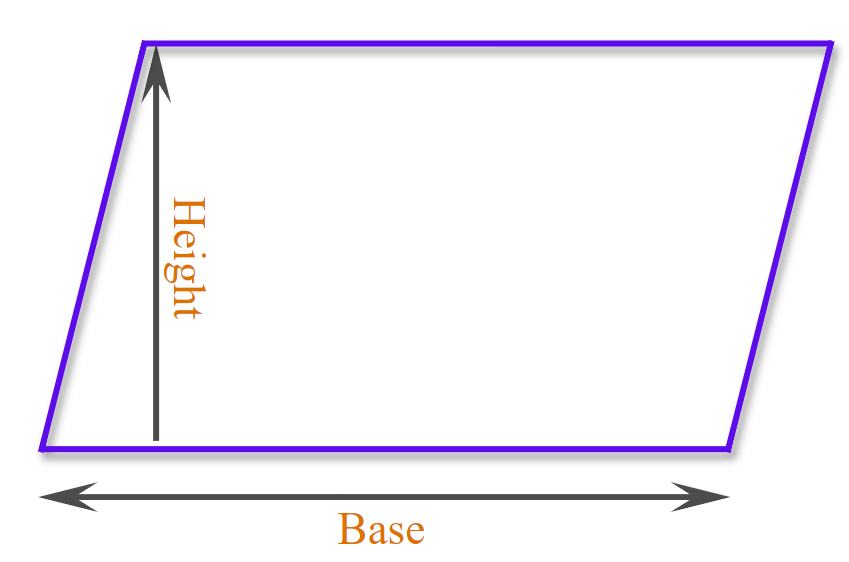
To find the area of a parallelogram, you can follow these steps:
- Choose a base (any one side of the parallelogram).
- Determine the height (the perpendicular distance from the base to the opposite side).
- Use the formula: Area = Base × Height

Let us understand this with an example:
Example 1: Find the area of the following parallelograms: 
Ans:
Base = 8 cm
Height = 3.5 cm
Area of parallelogram = Base × Height
Area of parallelogram = 8 cm x 3.5 cm = 28 cm2
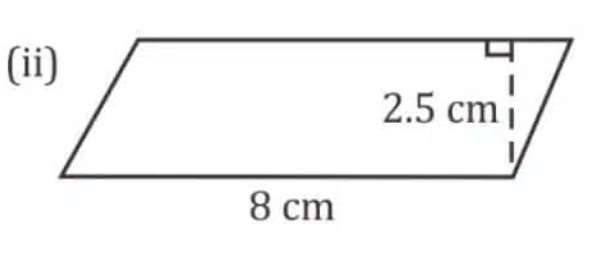
Ans:
Base = 8 cm
Height = 2.5 cm
Area of parallelogram = Base × Height
Area of parallelogram = 8 cm x 2.5 cm = 20 cm2
Example 2: PQRS is a parallelogram. QM is the height from Q to SR and QN is the height from Q to PS. If SR = 12 cm and QM = 7.6 cm. Find:
(a) the area of the parallelogram PQRS
(b) QN, if PS = 8 cm
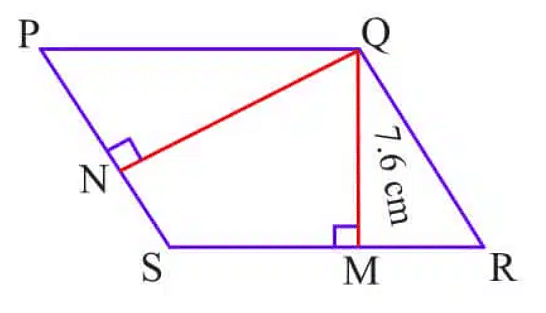
Ans:
Given: SR=12 cm, QM = 7.6 cm, PS = 8cm
(a) Area of parallelogram = base x height = 12 x 7.6 = 91.2 cm2
(b) Area of parallelogram = base x height
=> 91.2 = 8 x QN
=> QN = 91.2/8
= 11.4 cm.
Area of Triangle
A triangle is a polygon with three vertices, and three sides or edges that are line segments. A triangle with vertices A, B, and C is denoted as ABC.
 Triangle ABC
Triangle ABC
To find the area of a triangle within a parallelogram, you can follow these steps
1. Identify the Triangle
- Look at one of the triangles inside the parallelogram.
- The base of the triangle is one side of the parallelogram.
- The height is the straight distance from the base to the opposite side.
2. Understand the Relationship
- A parallelogram is made up of two identical triangles.
- Therefore, the area of the parallelogram is twice the area of one triangle.
3. Calculate the Area of the Parallelogram
- Use the formula: Area = Base × Height

4. Apply the Relationship for the Triangle
- Since the parallelogram has two identical triangles, the area of one triangle is half the area of the parallelogram.
12×Are
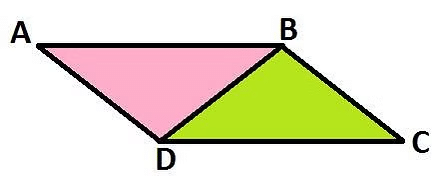 Parallelogram ABCD
Parallelogram ABCD
Area of each triangle = (Area of parallelogram)
= (base × height) (Since area of a parallelogram = base × height)
=(or , in short)
All the congruent triangles are equal in area but the triangles equal in area need not be congruent.
Example 1: Find BC, if the area of the triangle ABC is 36 cm2 and the height AD is 3 cm.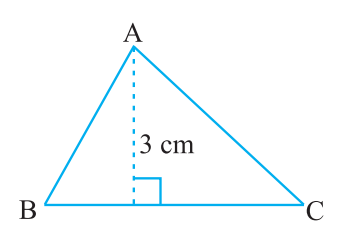
Ans:
Height = 3 cm, Area = 36 cm2
Area of the triangle ABC = 1/2 x b x h
=> 36 = 1/2 x b x 3 => b = 24 cm
Base BC = 24 cm
Example 2: Triangle ABC is isosceles with AB = AC = 7.5 cm and BC = 9 cm. The height AD from A to BC, is 6 cm. Find the area of Triangle ABC. What will be the height from C to AB i.e., CE?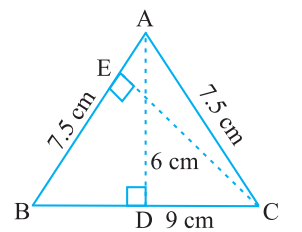
Ans:
In triangle ABC, AD = 6cm and BC = 9cm
Area of triangle = 1/2 x base x height = 1/2 x AB x CE
=> 27 = 1/2 x 7.5 x CE
=> CE = (27 x 2) /7.5 => CE = 7.2 cm
Height from C to AB ie.., CE is 7.2 cm
Circles
A circle is defined as a collection of points on a plane that are at an equal distance.
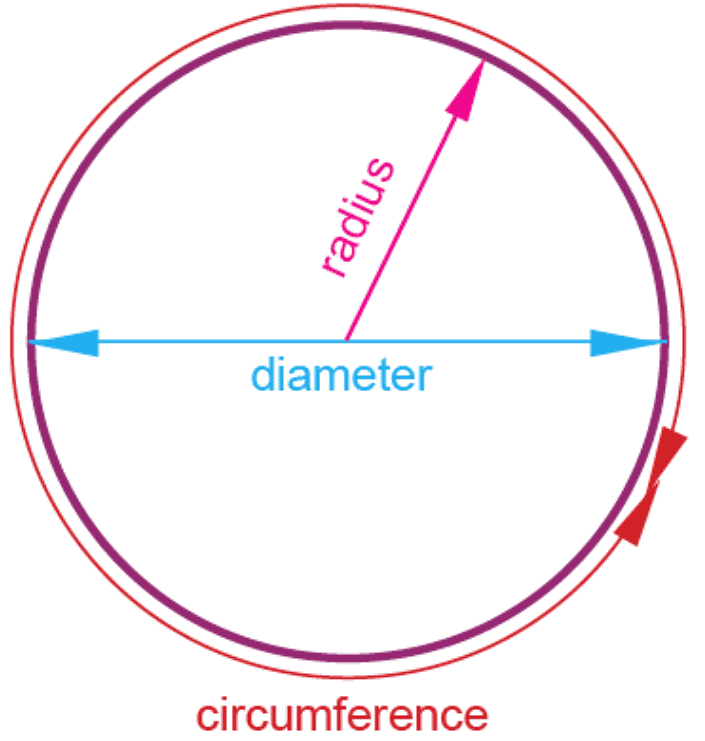 Circle
Circle
- Diameter: Any straight line segment that passes through the centre of a circle and whose end points are on the circle is called its diameter.
- Radius: Any line segment from the centre of the circle to its circumference.
Circumference of Circle
The distance around a circular region is known as its circumference.
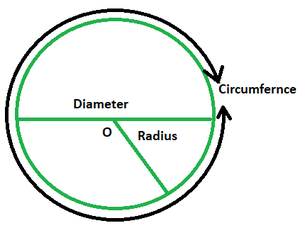

where,
- r is the radius of the circle
- π is an irrational number, whose value is approximately equal to 3.14 or it can be taken as 22/7
Diameter(d) of a circle is equal to twice the radius(r) =2r
Therefore, Circumference = Diameter x π
C = π d
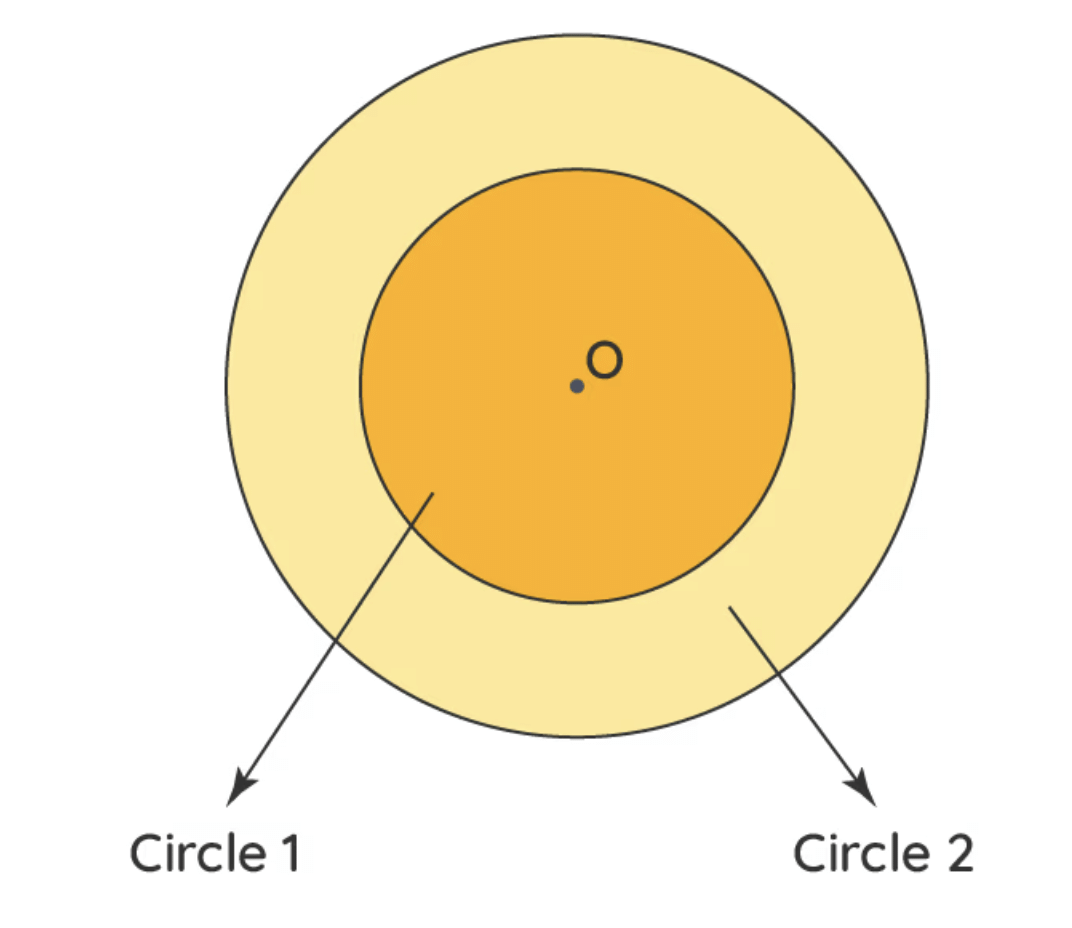
Note: Circles with the same centre but different radii are called concentric circles.
Example: If the radius of the circle is 25 units, find the circumference of the circle. (Take π = 3.14)
Ans:
Given, radius = 25 units
Let us write the circumference formula and then we will substitute the value of r (radius) in it.
Circumference of circle formula = 2πr
C = 2 × π × 25
C = 2 × 3.14 × 25 = 157 units
Therefore, the circumference of a circle is 157 units.
Area of Circle
The area of a circle is the region enclosed in the circle.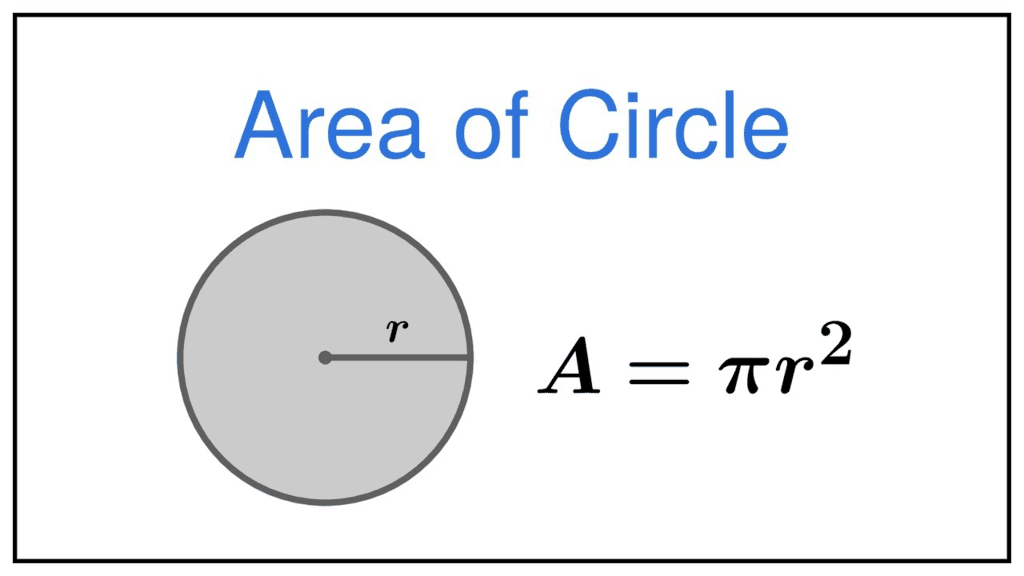
where
- r is the radius of the circle
- A is the area of the circle
- π is an irrational number, whose value is approximately equal to 3.14 or it can be taken as 22/7
Example 1: The radius of a circular pipe is 10 cm. What length of a tape is required to wrap once around the pipe (π = 3.14)?
Ans:
Radius of the pipe (r) = 10 cm
Length of tape required is equal to the circumference of the pipe. Circumference of the pipe = 2πr = 2 × 3.14 × 10 cm = 62.8 cm
Therefore, length of the tape needed to wrap once around the pipe is 62.8 cm.
Example 2: Find the perimeter of the given shape (Take π = 22/7 ).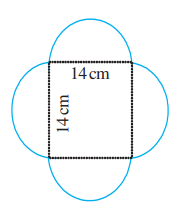
Ans: In this shape, we need to find the circumference of semicircles on each side of the square.Circumference of the circle = πd
Circumference of the semicircle = 1/2 πd = 1/2 x 22/7 × 14 cm = 22 cm Circumference of each of the semicircles is 22 cm .Therefore, the perimeter of the given figure = 4 × 22 cm = 88 cm.
Example 3: Diameter of a circular garden is 9.8 m. Find its area.
Ans:
Diameter, d = 9.8 m
Therefore, radius r = 9.8 ÷ 2 = 4.9 m
Area of the circle = πr2 = 22/7 x (4.9)2 m2 = 22/7 × 4.9 x 4.9 m2= 75.46 m2
Example 4:The adjoining figure shows two circles with the same centre. The radius of the larger circle is 10 cm and the radius of the smaller circle is 4 cm. Find: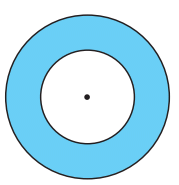
(a) the area of the larger circle
(b) the area of the smaller circle
(c) the shaded area between the two circles. (π = 3.14)
Ans:
(a) Radius of the larger circle = 10 cm So, area of the larger circle = πr2 = 3.14 × 10 × 10 = 314 cm2
(b) Radius of the smaller circle = 4 cm Area of the smaller circle = πr2 = 3.14 × 4 × 4 = 50.24 cm2
(c) Area of the shaded region = (314 – 50.24) cm2 = 263.76 cm2
|
76 videos|452 docs|39 tests
|
FAQs on Perimeter and Area Class 7 Notes Maths Chapter 9
| 1. What is the formula to calculate the area of a parallelogram? |  |
| 2. How do you find the area of a triangle? |  |
| 3. What is the formula for the circumference of a circle? |  |
| 4. How do you calculate the area of a circle? |  |
| 5. What is the difference between perimeter and area? |  |