NCERT Solutions for Class 7 Maths - Rational Numbers
Exercise 8.1
Q1: List five rational numbers between:
(i) -1 and 0
Ans: Let us write -1 and 0 as rational numbers with denominator 6.
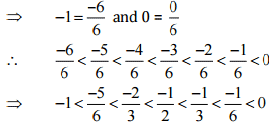
Therefore, five rational numbers between -1 and 0 would be
(ii) -2 and -1
Ans: Let us write -2 and -1 as rational numbers with denominator 6.
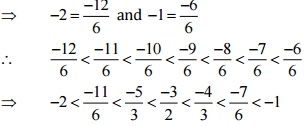
Therefore, Five rational numbers between -2 and -1 would be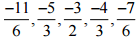
(iii) 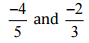
Ans: Let us write 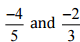 as rational numbers with the same denominators.
as rational numbers with the same denominators.
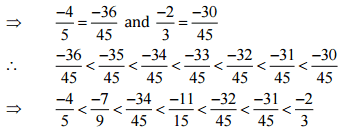
Therefore, five rational numbers between 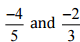 would be
would be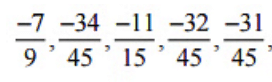
(iv) 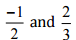
Ans: Let us write 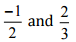 as rational numbers with the same denominators.
as rational numbers with the same denominators.
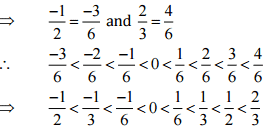
Therefore, five rational numbers between 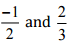 would be
would be 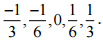
Q2: Write four more rational numbers in each of the following patterns:
(i) 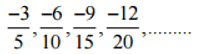
Ans: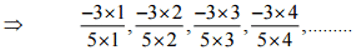
Therefore, the next four rational numbers of this pattern would be
(ii) 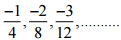
Ans: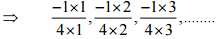
Therefore, the next four rational numbers of this pattern would be
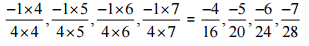
(iii) 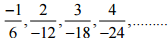
Ans:
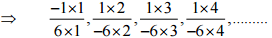
Therefore, the next four rational numbers of this pattern would be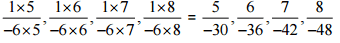
(iv) 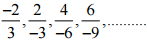
Ans: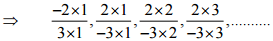
Therefore, the next four rational numbers of tins pattern would be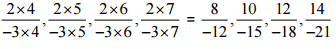
Q3: Give four rational numbers equivalent to:
(i) -2/7
Ans: The four rational numbers equivalent to -2/7 are,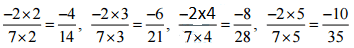
Therefore, four equivalent rational numbers are 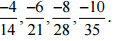
(ii) 5/-3
Ans: The four rational numbers equivalent to 5/-3 are,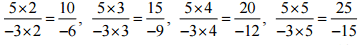
Therefore, four equivalent rational numbers are 
(iii) 4/9
Ans: The four rational numbers equivalent to 5/-3 are,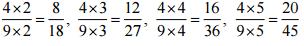
Therefore, four equivalent rational numbers are 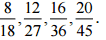
Q4: Draw the number line and represent the following rational numbers on it:
(i) 3/4
Ans: We know that 3/4 is greater than 0 and less than 1.
∴ it lies between 0 and 1. It can be represented on number line as,
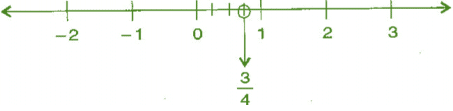
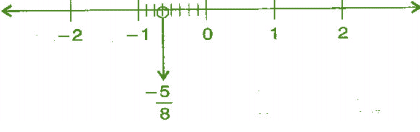
(ii) -5/8
Ans: We know that -5/8 is less than 0 and greater than -1.
∴ it lies between 0 and -1. It can be represented on number line as,
(iii) -7/4
Ans: Now above question can be written as,
= (-7/4) = 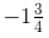
We know that (-7/4) is Less than -1 and greater than -2.
∴ it lies between -1 and -2. It can be represented on number line as,
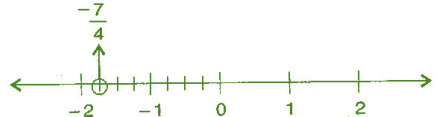
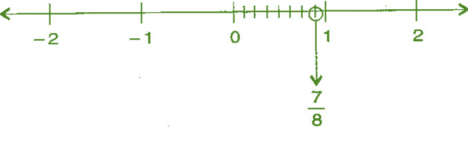
(iv) 7/8
Ans: We know that 7/8 is greater than 0 and less than 1.
∴ it lies between 0 and 1. It can be represented on number line as,
Q5: The points P, Q, R, S, T, U, A and B on the number line are such that, TR = RS = SU and AP = PQ = QB. Name the rational numbers represented by P, Q, R and S. 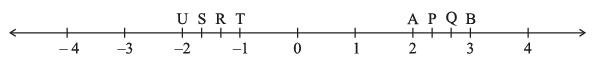
Ans:

Q6: Which of the following pairs represent the same rational numbers:
(i) 
Ans: We have to check the given pair represents the same rational number.
Then,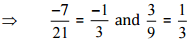 [Converting into lowest term]
[Converting into lowest term]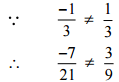
So, the given pair is not represents the same rational number.
(ii) 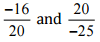
Ans: We have to check the given pair represents the same rational number.
Then,
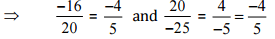 [Converting into lowest term]
[Converting into lowest term]
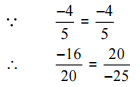
So, the given pair is represents the same rational number.
(iii) 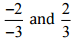
Ans: We have to check the given pair represents the same rational number.
Then,
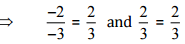 [Converting into lowest term]
[Converting into lowest term]
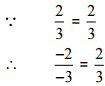
So, the given pair is represents the same rational number.
(iv) 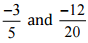
Ans: We have to check the given pair represents the same rational number.
Then,
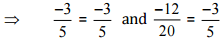 [Converting into lowest term]
[Converting into lowest term]
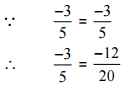
So, the given pair is represents the same rational number.
(v) 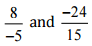
Ans: We have to check the given pair represents the same rational number.
Then,
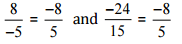 [Converting into lowest term]
[Converting into lowest term]
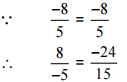
So, the given pair is represents the same rational number.
(vi) 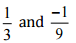
Ans: We have to check the given pair represents the same rational number.
Then,
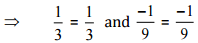 [Converting into lowest term]
[Converting into lowest term]
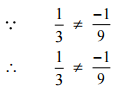
So, the given pair does not represent the same rational number.
(vii) 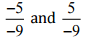
Ans: We have to check the given pair represents the same rational number.
Then,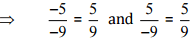 [Converting into lowest terra]
[Converting into lowest terra]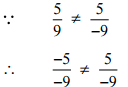
So, the given pair does not represent the same rational number.
Q7: Rewrite the following rational numbers in the simplest form:
(i) -8/6
Ans: The given rational numbers can be simplified further,
Then,
= -4/3 … [∵ Divide both numerator and denominator by 2]
(ii) 25/45
Ans: The given rational numbers can be simplified further,
Then,
= 5/9 … [∵ Divide both numerator and denominator by 5]
(iii) -44/72
Ans: The given rational numbers can be simplified further,
Then,
= -11/18 … [∵ Divide both numerator and denominator by 4]
(iv) -8/10
Ans: The given rational numbers can be simplified further,
Then,
= -4/5 … [∵ Divide both numerator and denominator by 2]
Q8: Fill in the boxes with the correct symbol out of <, > and =:
(i) 
Ans: The LCM of the denominators 7 and 3 is 21
∴ (-5/7) = [(-5 × 3)/ (7 × 3)] = (-15/21)
And (2/3) = [(2 × 7)/ (3 × 7)] = (14/21)
Now, -15 < 14
So,
(-15/21) < (14/21)
Hence, -5/7 [<] 2/3
(ii) 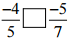
Ans: The LCM of the denominators 5 and 7 is 35
∴ (-4/5) = [(-4 × 7)/ (5 × 7)] = (-28/35)
And (-5/7) = [(-5 × 5)/ (7 × 5)] = (-25/35)
Now, -28 < -25
So,
(-28/35) < (- 25/35)
Hence, -4/5 [<] -5/7
(iii) 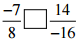
Ans: 14/-16 can be simplified further,
Then,
7/-8 … [∵ Divide both numerator and denominator by 2]
So,
(-7/8) = (-7/8)
Hence, -7/8 [=] 14/-16
(iv) 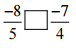
Ans: The LCM of the denominators 5 and 4 is 20
∴ (-8/5) = [(-8 × 4)/ (5 × 4)] = (-32/20)
And (-7/4) = [(-7 × 5)/ (4 × 5)] = (-35/20)
Now, -32 > – 35
So,
(-32/20) > (- 35/20)
Hence, -8/5 [>] -7/4
(v) 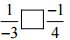
Ans: The LCM of the denominators 3 and 4 is 12
∴ (-1/3) = [(-1 × 4)/ (3 × 4)] = (-4/12)
And (-1/4) = [(-1 × 3)/ (4 × 3)] = (-3/12)
Now, -4 < – 3
So,
(-4/12) < (- 3/12)
Hence, 1/-3 [<] -1/4
(vi) 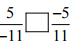
Ans: Since, (-5/11) = (-5/11)
Hence, 5/-11 [=] -5/11
(vii) 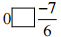
Ans: Since every negative rational number is less than 0.
We have:
= 0 [>] -7/6
Q9: Which is greater in each of the following:
(i) 
Ans: The LCM of the denominators 3 and 2 is 6
(2/3) = [(2 × 2)/ (3 × 2)] = (4/6)
And (5/2) = [(5 × 3)/ (2 × 3)] = (15/6)
Now, 4 < 15
So, (4/6) < (15/6)
∴ 2/3 < 5/2
Hence, 5/2 is greater.
(ii) 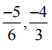
Ans: The LCM of the denominators 6 and 3 is 6
∴ (-5/6) = [(-5 × 1)/ (6 × 1)] = (-5/6)
And (-4/3) = [(-4 × 2)/ (3 × 2)] = (-12/6)
Now, -5 > -12
So, (-5/6) > (- 12/6)
∴ -5/6 > -12/6
Hence, – 5/6 is greater.
(iii) 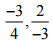
Ans: The LCM of the denominators 4 and 3 is 12
∴ (-3/4) = [(-3 × 3)/ (4 × 3)] = (-9/12)
And (-2/3) = [(-2 × 4)/ (3 × 4)] = (-8/12)
Now, -9 < -8 So, (-9/12) < (- 8/12)
∴ -3/4 < 2/-3
Hence, 2/-3 is greater.
(iv) 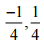
Ans: The given fraction is like friction,
So, -¼ < ¼
Hence ¼ is greater,
(v) 
Ans: First we have to convert mixed fractions into improper fractions,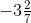 = -23/7
= -23/7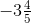 = -19/5
= -19/5
Then, The LCM of the denominators 7 and 5 is 35
∴ (-23/7) = [(-23 × 5)/ (7 × 5)] = (-115/35)
And (-19/5) = [(-19 × 7)/ (5 × 7)] = (-133/35)
Now, -115 > -133 So, (-115/35) > (- 133/35)
∴ 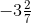 >
> 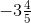
Hence, 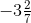 is greater.
is greater.
Q10: Write the following rational numbers in ascending order:
(i) -3/5, -2/5, -1/5
Ans: The given rational numbers are in form of like fractions,
Hence, (-3/5)< (-2/5) < (-1/5)
(ii) -1/3, -2/9, -4/3
Ans: To convert the given rational numbers into like fractions we have to find LCM,
LCM of 3, 9, and 3 is 9
Now,
(-1/3)= [(-1 × 3)/ (3 × 9)] = (-3/9)
(-2/9)= [(-2 × 1)/ (9 × 1)] = (-2/9)
(-4/3)= [(-4 × 3)/ (3 × 3)] = (-12/9)
Clearly, (-12/9) < (-3/9) < (-2/9)
Hence, (-4/3) < (-1/3) < (-2/9)
(iii) -3/7, -3/2, -3/4
Ans: To convert the given rational numbers into like fractions we have to find LCM,
LCM of 7, 2, and 4 is 28
Now, (-3/7)= [(-3 × 4)/ (7 × 4)] = (-12/28)
(-3/2)= [(-3 × 14)/ (2 × 14)] = (-42/28)
(-3/4)= [(-3 × 7)/ (4 × 7)] = (-21/28)
Clearly, (-42/28) < (-21/28) < (-12/28)
Hence, (-3/2) < (-3/4) < (-3/7)
Exercise 8.2
Q1: Find the sum:
(i) 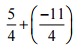
Ans: We have:
= (5/4) – (11/4) = [(5 – 11)/4] … [∵ denominator is same in both the rational numbers]
= (-6/4)
= -3/2 … [∵ Divide both numerator and denominator by 3]
(ii) 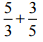
Ans: Take the LCM of the denominators of the given rational numbers.
LCM of 3 and 5 is 15 Express each of the given rational numbers with the above LCM as the common denominator.
Now, (5/3) = [(5 × 5)/ (3 × 5)] = (25/15)
(3/5) = [(3 × 3)/ (5 × 3)] = (9/15)
Then,
= (25/15) + (9/15) … [∵ denominator is same in both the rational numbers]
= (25 + 9)/15 = 34/15
(iii) 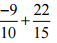
Ans: Take the LCM of the denominators of the given rational numbers.
LCM of 10 and 15 is 30 Express each of the given rational numbers with the above LCM as the common denominator.
Now,
(-9/10)= [(-9 × 3)/ (10 × 3)] = (-27/30)
(22/15)= [(22 × 2) / (15 × 2)] = (44/30)
Then, = (-27/30) + (44/30) … [∵ denominator is same in both the rational numbers]
= (-27 + 44)/30
= (17/30)
(iv) 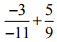
Ans: We have, = 3/11 + 5/9
Take the LCM of the denominators of the given rational numbers.
LCM of 11 and 9 is 99
Express each of the given rational numbers with the above LCM as the common denominator.
Now,
(3/11) = [(3 × 9)/ (11 × 9)] = (27/99)
(5/9) = [(5 × 11)/ (9 × 11)] = (55/99)
Then,
= (27/99) + (55/99) … [∵ denominator is same in both the rational numbers]
= (27 + 55)/99
= (82/99)
(v) 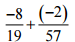
Ans: We have = -8/19 – 2/57
Take the LCM of the denominators of the given rational numbers.
LCM of 19 and 57 is 57
Express each rational number with the above LCM as the common denominator.
Now,
(-8/19)= [(-8 × 3)/ (19 × 3)] = (-24/57) (-2/57)= [(-2 × 1)/ (57 × 1)] = (-2/57)
Then,
= (-24/57) – (2/57) … [∵ denominator is same in both the rational numbers]
= (-24 – 2)/57 = (-26/57)
(vi) 
Ans: We know that any number or fraction is added to zero the answer will be the same number or fraction.
Hence,
= -2/3 + 0
= -2/3
(vii) 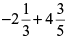
Ans: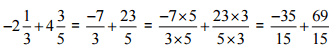 [L.C.M. of 3 and 5 is 15]
[L.C.M. of 3 and 5 is 15]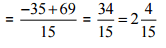
Q2: Find:
(i) 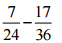
Ans: Take the LCM of the denominators of the given rational numbers.
LCM of 24 and 36 is 72
Express each of the given rational numbers with the above LCM as the common denominator.
Now,
(7/24)= [(7 × 3)/ (24 × 3)] = (21/72)
(17/36)= [(17 × 2)/ (36 × 2)] = (34/72)
Then,
= (21/72) – (34/72) … [∵ denominator is same in both the rational numbers]
= (21 – 34)/72 = (-13/72)
(ii)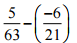
Ans: We can also write -6/21 = -2/7
= 5/63 – (-2/7)
We have, = 5/63 + 2/7
Take the LCM of the denominators of the given rational numbers.
LCM of 63 and 7 is 63
Express each of the given rational numbers with the above LCM as the common denominator.
Now,
(5/63)= [(5 × 1)/ (63 × 1)] = (5/63)
(2/7)= [(2 × 9)/ (7 × 9)] = (18/63)
Then, = (5/63) + (18/63) … [∵ denominator is same in both the rational numbers]
= (5 + 18)/63 = 23/63
(iii)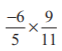
Ans: We have, = -6/13 + 7/15
LCM of 13 and 15 is 195
Express each of the given rational numbers with the above LCM as the common denominator.
Now,
(-6/13)= [(-6 × 15)/ (13 × 15)] = (-90/195)
(7/15)= [(7 × 13)/ (15 × 13)] = (91/195)
Then, = (-90/195) + (91/195) … [∵ denominator is same in both the rational numbers]
= (-90 + 91)/195
= (1/195)
(iv) 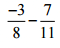
Ans: Take the LCM of the denominators of the given rational numbers.
LCM of 8 and 11 is 88
Express each of the given rational numbers with the above LCM as the common denominator.
Now,
(-3/8)= [(-3 × 11)/ (8 × 11)] = (-33/88)
(7/11)= [(7 × 8)/ (11 × 8)] = (56/88)
Then, = (-33/88) – (56/88) … [∵ denominator is same in both the rational numbers]
= (-33 – 56)/88
= (-89/88)
(v) 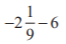
Ans: First we have to convert the mixed fraction into improper fraction,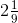 = -19/9
= -19/9
We have, -19/9 – 6
Take the LCM of the denominators of the given rational numbers.
LCM of 9 and 1 is 9
Express each of the given rational numbers with the above LCM as the common denominator.
Now,
(-19/9)= [(-19 × 1)/ (9 × 1)] = (-19/9)
(6/1)= [(6 × 9)/ (1 × 9)] = (54/9)
Then, = (-19/9) – (54/9) … [∵ denominator is same in both the rational numbers]
= (-19 – 54)/9
= (-73/9)
Q3: Find the product:
(i) (9/2) × (-7/4)
Ans: The product of two rational numbers = (product of their numerator)/ (product of their denominator)
The above question can be written as
(9/2) × (-7/4)
We have,
= (9 × -7) / (2 × 4)
= -63/8
(ii) (3/10) × (-9)
Ans: The product of two rational numbers = (product of their numerator)/ (product of their denominator)
The above question can be written as
(3/10) × (-9/1)
We have,
= (3 × -9)/ (10×1)
= -27/10
(iii) (-6/5) × (9/11)
Ans: The product of two rational numbers = (product of their numerator)/ (product of their denominator)
We have,
= (-6 × 9) / (5 × 11)
= -54/55
(iv) (3/7) × (-2/5)
Ans: The product of two rational numbers = (product of their numerator)/ (product of their denominator)
We have,
= (3 × -2) / (7 × 5)
= -6/35
(v) (3/11) × (2/5)
Ans: The product of two rational numbers = (product of their numerator)/ (product of their denominator)
We have,
= (3 × 2) / (11 × 5)
= 6/55
(vi) (3/-5) × (-5/3)
Ans: The product of two rational numbers = (product of their numerator)/ (product of their denominator)
We have,
= (3 × -5) / (-5 × 3)
On simplifying, = (1 × -1)/ (-1 × 1)
= -1/-1 = 1
Q4: Find the value of:
(i) (-4) ÷ (2/3)
Ans: We have,
= (-4/1) × (3/2) … [∵ reciprocal of (2/3) is (3/2)]
The product of two rational numbers = (product of their numerator)/ (product of their denominator)
= (-4 × 3) / (1 × 2) = (-2 × 3) / (1 × 1) = -6
(ii) (-3/5) ÷ 2
Ans: We have,
= (-3/5) × (1/2) … [∵ reciprocal of (2/1) is (1/2)]
The product of two rational numbers = (product of their numerator)/ (product of their denominator)
= (-3 × 1) / (5 × 2)
= -3/10
(iii) (-4/5) ÷ (-3)
Ans: We have,
= (-4/5) × (1/-3) … [∵ reciprocal of (-3) is (1/-3)]
The product of two rational numbers = (product of their numerator)/ (product of their denominator)
= (-4× (1)) / (5× (-3))
= -4/-15 = 4/15
(iv) (-1/8) ÷ 3/4
Ans: We have,
= (-1/8) × (4/3) … [∵ reciprocal of (3/4) is (4/3)]
The product of two rational numbers = (product of their numerator)/ (product of their denominator)
= (-1 × 4) / (8 × 3)
= (-1 × 1) / (2 × 3) = -1/6
(v) (-2/13) ÷ 1/7
Ans: We have,
= (-2/13) × (7/1) … [∵ reciprocal of (1/7) is (7/1)]
The product of two rational numbers = (product of their numerator)/ (product of their denominator)
= (-2 × 7) / (13 × 1)
= -14/13
(vi) (-7/12) ÷ (-2/13)
Ans: We have, = (-7/12) × (13/-2) … [∵ reciprocal of (-2/13) is (13/-2)]
The product of two rational numbers = (product of their numerator)/ (product of their denominator)
= (-7× 13) / (12× (-2))
= -91/-24 = 91/24
(vii) (3/13) ÷ (-4/65)
Ans: We have, = (3/13) × (65/-4) … [∵ reciprocal of (-4/65) is (65/-4)]
The product of two rational numbers = (product of their numerator)/ (product of their denominator)
= (3 × 65) / (13 × (-4))
= 195/-52 = -15/4
|
76 videos|452 docs|39 tests
|
FAQs on NCERT Solutions for Class 7 Maths - Rational Numbers
| 1. What are rational numbers and how are they represented? |  |
| 2. How do you add and subtract rational numbers? |  |
| 3. Can you provide an example of multiplying rational numbers? |  |
| 4. What is the process for dividing rational numbers? |  |
| 5. How do you convert a decimal to a rational number? |  |






















