NCERT Solutions for Class 8 Maths Chapter 5 - Understanding Elementary Shapes (Exercise 5.4, 5.5 and 5.6)
Exercise 5.4
Q1. What is the measure of
(i) a right angle?
Ans: The measure of a right angle is 90o
(ii) a straight angle?
Ans: The measure of a straight angle is 180o
Q2. Say True or False:
(a) The measure of an acute angle < 90°.
(b) The measure of an obtuse angle < 90°.
(c) The measure of a reflex angle > 180°.
(d) The measure of on complete revolution = 360°.
(e) If m∠A = 53o and m∠B = 35o then m∠A > m∠B.
Ans:
(a) True; the measure of an acute angle is less than 90o
(b) False; the measure of an obtuse angle is more than 90o but less than 180o
(c) True; the measure of a reflex angle is more than 180o
(d) True; the measure of one complete revolution is 360o
(e) True; ∠A is greater than ∠B
Q3. Write down the measure of:
(a) some acute angles
(b) some obtuse angles
(give at least two examples of each)
Ans: (a) The measures of an acute angle are 50°, 65°
(b) The measures of obtuse angle are 110°, 175°
Q4. Measure the angles given below using the Protractor and write down the measure: 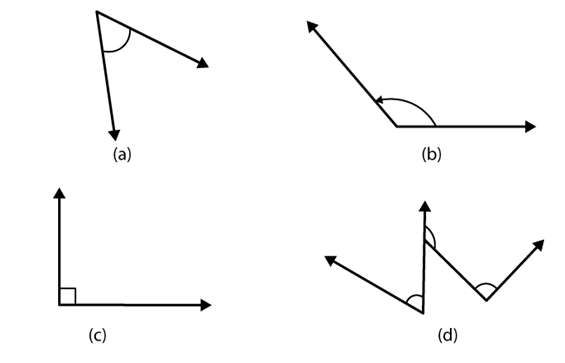
Ans: (a) The measure of an angle is 45°
(b) The measure of an angle is 120°
(c) The measure of an angle is 90°
(d) The measures of angles are 60°, 90° and 130°
Q5. Which angle has a large measure? First estimate and then measure:
Measure of angle A = ?
Measure of angle B = ?
Ans: ∠B has larger measure.
∠A = 40o and ∠B = 68o
Q6. From these two angles which has larger measure? Estimate and then confirm by measuring them:
Ans: Second angle has larger measure.
The measures of these angles are 45o and 55o.
Q7. Fill in the blanks with acute, obtuse, right or straight:
(a) An angle whose measure is less than that of a right angle is ________________.
Ans: acute angle
(b) An angle whose measure is greater than that of a right angle is ________________.
Ans: obtuse angle
(c) An angle whose measure is the sum of the measures of two right angles is ________________.
Ans: straight angle
(d) When the sum of the measures of two angles is that of a right angle, then each one of them is ________________.
Ans: acute angle
(e) When the sum of the measures of two angles is that of a straight angle and if one of them is acute then the other should be ________________.
Ans: obtuse angle
Q8. Find the measure of the angle shown in each figure. (First estimate with your eyes and then find the actual measure with a protractor.) 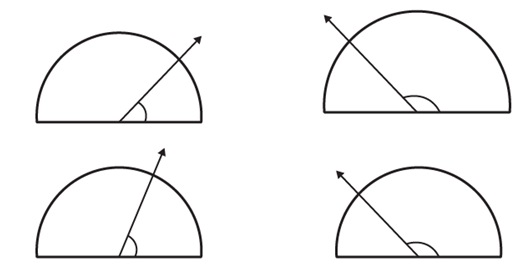 Ans: The measures of the angles shown in the above figures are 40o, 130o, 65o and 135o
Ans: The measures of the angles shown in the above figures are 40o, 130o, 65o and 135o
Q9. Find the angle measure between the hands of the clock in each figure:
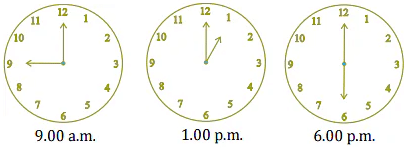 Ans: (i) 90 (Right angle)
Ans: (i) 90 (Right angle)
(ii) 30 (Acute angle)
(iii) 180 (Straight angle)
Q10. Investigate:
In the given figure, the angle measure 30o. Look at the same figure through a magnifying glass. Does the angle becomes larger? Does the size of the angle change?
Ans: No, the measure of angle will be same.
Q11. Measure and classify each angle:
 Ans:
Ans: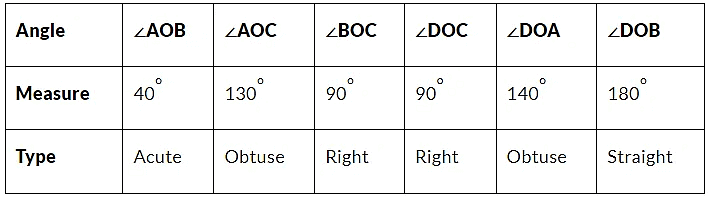
Exercise 5.5
Q1. Which of the following are models for perpendicular lines:
(a) The adjacent edges of a table top.
(b) The lines of a railway track.
(c) The line segments forming the letter ‘L’.
(d) The letter V.
Ans:
(a) Perpendicular
(b) Not perpendicular
(c) Perpendicular
(d) Not perpendicular
Q2. Let be the perpendicular to the line segment
. Let
and
intersect in the point A. What is the measure of ∠PAY?
Ans: We will be using the concept of perpendicular lines to solve this.
Since PQ ⊥ XY Therefore, ∠PAY = 90°
Q3. There are two “set-squares” in your box. What are the measures of the angles that are formed at their corners? Do they have any angle measure that is common?
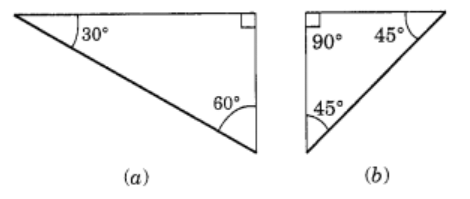
Ans: One set-square has 60°,90°, 30° and other set-square has 45° ,90° ,45°. They have 90° as common angle.
Q4. Study the diagram. The line l is perpendicular to line m.
(a) Is CE = EG?
(b) Does PE bisect CG?
(c) Identify any two line segments for which PE is the perpendicular bisector.
(d) Are these true?
(i) AC > FG
(ii) CD = GH
(iii) BC < EH
Ans: (a) Yes, both measure 2 units.
(b) Yes, because CE = EG
(d) (i) True, (ii) True, (iii) True
Exercise 5.6
Q1. Name the types of following triangles:
(a) Triangle with lengths of sides 7 cm, 8 cm and 9 cm.
(b) ΔABC with AB = 8.7 cm, AC = 7 cm and BC = 6 cm.
(c) ΔPQR such that PQ = QR = PR = 5 cm.
(d) ΔDEF with m∠D = 90o
(e) ΔXYZ with m∠Y = 90o and XY = YZ
(f) ΔLMN with m∠L = 30o , m∠M = 70o and m∠N = 80o.
Ans: (a) Scalene triangle
(b) Scalene triangle
(c) Equilateral triangle
(d) Right-angled triangle
(e) Isosceles right-angled triangle
(f) Acute-angled triangle
Q2. Match the following:
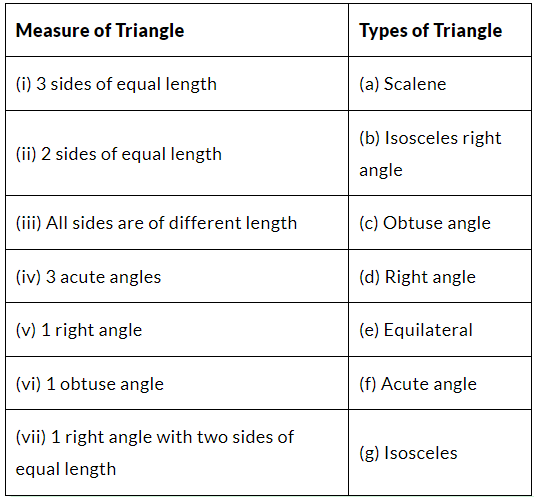 Ans: (i) → (e)
Ans: (i) → (e)
(ii) → (g)
(iii) → (a)
(iv) → (f)
(v) → (d)
(vi) → (c)
(vii) → (b)
Q3. Name each of the following triangles in two different ways: (You may judge the nature of angle by observation) 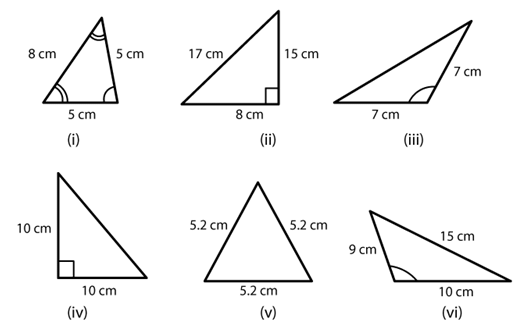
Ans: (i) Acute-angled and isosceles triangle
(ii) Right-angled and scalene triangle
(iii) Obtuse-angled and isosceles triangle
(iv) Right-angled and isosceles triangle
(v) Equilateral and acute-angled triangle
(vi) Obtuse-angled and scalene triangle
Q4. Try to construct triangles using match sticks. Some are shown here.
Can you make a triangle with:
(a) 3 matchsticks?
(b) 4 matchsticks?
(c) 5 matchsticks?
(d) 6 matchsticks?
(Remember you have to use all the available matchsticks in each case)
If you cannot make a triangle, think of reasons for it.
Ans: (a) 3 matchsticks This is an acute angle triangle and it is possible with 3 matchsticks to make a triangle because sum of two sides is greater than third side.
(b) 4 matchsticks This is a square, hence with four matchsticks we cannot make triangle.
(c) 5 matchsticks This is an acute angle triangle and it is possible to make triangle with five matchsticks, in this case sum of two sides is greater than third side.
(d) 6 matchsticks This is an acute angle triangle and it is possible to make a triangle with the help of 6 matchsticks because sum of two sides is greater than third side.
|
82 videos|273 docs|69 tests
|
FAQs on NCERT Solutions for Class 8 Maths Chapter 5 - Understanding Elementary Shapes (Exercise 5.4, 5.5 and 5.6)
| 1. What are some examples of elementary shapes? |  |
| 2. How are elementary shapes useful in everyday life? |  |
| 3. How can elementary shapes be used to teach children about geometry? |  |
| 4. What is the difference between a regular and irregular polygon? |  |
| 5. How can understanding elementary shapes help with problem-solving? |  |

















