Class 10 Mathematics: CBSE Sample Question Paper- Term II (2021-22) - 2 | CBSE Sample Papers For Class 10 PDF Download
| Table of contents |

|
| Class-X |

|
| Time: 120 |

|
| Minutes |

|
| M.M: 40 |

|
| Section - A |

|
| Section - B |

|
| Section - C |

|
Class-X
Time: 120
Minutes
M.M: 40
General Instructions:
Read the following instructions very carefully and strictly follow them:
- The question paper consists of 14 questions divided into 3 sections A, B, C.
- All questions are compulsory.
- Section A comprises of 6 questions of 2 marks each. Internal choice has been provided in two questions.
- Section B comprises of 4 questions of 3 marks each. Internal choice has been provided in one question.
- Section C comprises of 4 questions of 4 marks each. An internal choice has been provided in one question. It contains two case study based questions.
Section - A
Q.1. How many two digits numbers are divisible by 3?
OR
Find the number of natural numbers between 102 and 998 which are divisible by 2 and 5 both.
Lowest two digit number divisible by 3 is 12. and highest two digit number divisible by 3 is 99.
Hence, the sequence start with 12 and ends with 99 and common difference is 3.
So, the A.P. will be 12, 15, 18, ----, 96, 99.
Here, a = 12, d = 3, l = 99
∴ l = a + (n – 1)d
∴ 99 = 12 + (n – 1)3
⇒ 99 – 12 = 3(n – 1)
⇒ n – 1 = (87/3)
⇒ n – 1 = 29
⇒ n = 30
Therefore, there are 30, two digit numbers which are divisible by 3.
OR
The number which ends with 0 is divisible by 2 and 5 both.
∴ Such numbers between 102 and 998 are:
110, 120, 130, .........., 990.
Last term, an = 990
a + (n + 1)d = 990
110 + (n – 1) × 10 = 990 (∵ a = first term = 110)
110 + 10n – 10 = 990
10n + 100 = 990
10n = 990 – 100
10n = 890
n = 890/10 = 89.
Q.2. Solve the following quadratic equation for x:
9x2 – 9(a + b)x + 2a2 + 5ab + 2b2 = 0
Given,
9x2 – 9(a + b)x + 2a2 + 5ab + 2b2 = 0
First, we solve,
2a2 + 5ab + 2b2 = 2a2 + 4ab + ab + 2b2
Here, = 2a[a + 2b] + b[a + 2b]
= (a + 2b) (2a + b)
Hence, the equation becomes
9x2 – 9(a + b)x + (a + 2b)(2a + b) = 0
⇒ 9x2 – 3[3a + 3b]x + (a + 2b)(2a + b) = 0
⇒ 9x2 – 3[(a + 2b) + (2a + b)]x + (a + 2b)(2a +b) = 0
⇒ 9x2 – 3(a + 2b)x – 3(2a + b)x +(a + 2b) (2a + b)= 0
⇒ 3x[3x – (a + 2b)] – (2a + b) [3x – (a + 2b)] = 0
⇒ [3x – (a + 2b)][3x – (2a + b)] = 0
⇒ 3x – (a + 2b) = 0 or 3x – (2a + b) = 0
⇒ x = ((a + 2b)/3) or x = ((2a + b)/3)
Hence, the roots =
Q.3. Prove that the lengths of two tangents drawn from an external point to a circle are equal.
Given, AP and BP are tangents of circle having centre O.
To Prove : AP = BP
Construction : Join OP, AO and BO
Proof : In DOAP and DOBP
OA = OB (Radius of circle)
OP = OP (Common side)
∠OAP = ∠OBP = 90° (Radius ⊥ tangent)
ΔOAP ≅ ΔOBP (RHS congruency rule)
AP = BP (By cpct) 1.Hence Proved.
Q.4. The volume of a right circular cylinder with its height equal to the radius, is 25(1/7) cm3.
Find the height of the cylinder. (Use π = 22/7)
Given,
Volume of a right circular cylinder = 25(1/7) cm3
i.e., πr2h = 176/7
Since, r = h ...given
(22/7) x h2 x h = 176/7
⇒ h3 = 176/22 = 8 = 23.
Hence, height of the cylinder = 2 cm.
Q.5. Given below is the distribution of weekly pocket money received by students of a class. Calculate the pocket money that is received by most of the students.

Here, Modal Class = 80 – 100
l = 80, f1 = 18, f2 = 5, f0 = 12 and h = 20
∴ Mode = l +
= 80 + (6/19) x 20
= 80 + 6.31 = 86.31 (approx.)
Hence, mode = 86.31.
Q.6. For what value(s) of 'a' quadratic equation 3ax2 – 6x + 1 = 0 has no real roots ?
OR
If one root of the equation (k – 1)x2 – 10x + 3 = 0 is the reciprocal of the other, then find the value of k.
Given that,
3ax2 – 6x + 1 = 0
For no real roots b2 – 4ac < 0
Discriminant D < 0 so,
(– 6)2 – 4(3a) (1) < 0
12a > 36
a > 3
Detailed Solution:
Given, 3ax2 – 6x + 1 = 0
On Comparing with AX2 + BX + C = 0,
we get A = 3a, B = – 6 and C = 1
Discriminant, D = B2 – 4AC
= (– 6)2 – 4 × 3a × 1
= 36 – 12a
For condition of 'no real roots',
B2 – 4AC < 0
⇒ 36 – 12a < 0
⇒ 12a > 36
⇒ a > 3.
OR
Let one root = α
and the other root = 1/α
Product of roots = α x (1/α) = 1
Given equation, (k – 1)x2 – 10x + 3 = 0
Comparing it with standard quadratic equation ax2 + bx + c = 0
we get, a = (k – 1), b = – 10 & c = 3
Product of roots = c/a = 3/(k - 1)
1 = 3/(k - 1)
or, 3 = k – 1
or, k = 4.
Section - B
Q.7. Following is the distribution of the long jump competition in which 250 students participated. Find the median distance jumped by the students. Interpret the median
n/2 = 250/2
= 125 ⇒ median class is 2 – 3,
l = 2, h = 1, cf = 120, f = 62
Median =
= 2 + (5/62)
= 129/62 = 2(5/62) m or 2.08 m
50% of students jumped below 2(5/62) m and 50% above it.
Detailed Solution:
Take N/2 = 250/2 = 125
∴ Median class = 2 – 3
Lower limit of median class (l) = 2
Size of median class (h) = 1
Frequency corresponding to median class (f) = 62
Total number of observations
Frequency (N) = 250
Cumulative frequency preceding
Median class (c.f.) = 120
Median =
= 2 + (5/62)
= 129/62
= 2(5/62) m or 2.08 m
∴ 50% of students jumped below 2.08 m and 50% of students jumped above 2.08 m.
Q.8. Construct a pair of tangents to a circle of radius 4 cm, which are inclined to each other at an angle of 60°.
Draw circle of radius 4cm
Draw OA and construct ∠AOB = 120°
Draw ∠OBP = ∠OBP = 90°
PA and PB are required tangents
Detailed Solution:Steps of construction:
- Draw a circle of radius 4 cm.
- Draw two radii having an angle of 120°.
- Let the radii intersect circle at A and B.
- Draw angle of 90° on both A and B.
- The point where both rays of 90° intersect is P.
- PA and PB are the required tangents.
Q.9. The distribution given below shows the runs scored by batsmen in one-day cricket matches. Find the mean number of runs.
Mean
Q.10. Two vertical poles of different heights are standing 20 m away from each other on the level ground. The angle of elevation of the top of the first pole from the foot of the second pole is 60° and angle of elevation of the top of the second pole from the foot of the first pole is 30°. Find the difference between the heights of two poles. (Take √3 = 1.73)
OR
A boy 1.7 m tall is standing on a horizontal ground, 50 m away from a building. The angle of elevation of the top of the building from his eye is 60°. Calculate the height of the building. (Take √3 = 1.73)
In ∆PQS, tan60° = y/20
⇒ y = 20√3 m
In ∆RSQ, tan30° = x/20
⇒ x = (20/√3) m
y – x =
ORLet PR be the building and AB be the boy
In ∆PQR, tan 60° = PQ/50 ⇒ PQ = 50√3m
Height of the building = ( 50√3 +1.7 )m = = 88.2 mDetailed Solution:
Let the heights of two pole be y and x.
Distance between the poles is QS = 20 m.
In ∆PQS, ∠Q = 90°
tan 60° = PQ/QS
√3 =(y/20)
y = 20√3 m
In ∆RSQ, ∠S = 90°
tan 30° = RS/QS
1/√3 = x/20
20/√3 = x
x = (20/3)√3 m
Difference between their heights
= (20/3)√3 x 2
= (40/3)√3.
= 23.07m
ORHeight of Boy = AB = 1.7 m
= QR = 1.7 m
Distance between Boy and building
BR = 50 m
⇒ AQ = 50 m
In ∆PQA, ∠Q = 90°
tan 60° = PQ/AQ
√3 = PQ/50
50√3 = PQ
Total height of the building = PQ + QR
= 86.5 + 1.7 = 88.2 m.
Section - C
Q.11. A solid is in the shape of a cone mounted on a hemisphere of same base radius. If the curved surface areas of the hemispherical part and the conical part are equal, then find the ratio of the radius and the height of the conical part.
Let ABC be a cone, which is mounted on a hemisphere.
Given, OC = OD = r cm
Curved surface area of the hemispherical part = (1/2)4πr2
= 2pr2
Slant height of a cone,
and curved surface area of a cone = πrl
According to the problem,(Given)
⇒
on squaring both of the sides, we get
4r2 = h2 + r2
⇒ 4r2 – r2 = h2
⇒ 3r2 = h2
⇒
⇒
Hence, the ratio of the radius and the height of conical part = 1 : √3.
Q.12. PQ is a tangent to a circle with centre O at point P. If ΔOPQ is an isosceles triangle, then find ∠OQP.
OR
The radii of two concentric circles are 13 cm and 8 cm. AB is a diameter of the bigger circle and BD is a tangent to the smaller circle touching it at D and intersecting the larger circle at P on producing. Find the length of AP.
In ΔOPQ,
∠P+∠Q+∠O =180°
(∠O = ∠Q, isosceles triangle)
2∠Q+∠P = 180°
2∠Q+90° = 180°
2∠Q = 90°
∠Q = 45°
Detailed Solution:
Since, ∠OPQ = 90° (Angle between tangent and radius)
Let ∠PQO be x°, then ∠QOP = x°
(Since OPQ is an isosceles triangle) (OP = OQ) (given)In ΔOPQ,
∠OPQ + ∠PQO + ∠QOP = 180° (Sum of the angles of a triangle)
∴ 90° + x° + x° = 180°
⇒ 2x° = 180° – 90° = 90°
⇒ x = 90°/2 = 45°.
Hence, ∠OQP is 45°.
OR∠APB = 90° (angle in semi-circle) and ∠ODB = 90° (radius is perpendicular to tangent)
ΔABP ~ ΔOBD
⇒
⇒ 26/13 = AP/8
Hence, AP = 16 cm.
Case Study-1
Q.13. ‘Skysails’ is that genre of engineering science that uses extensive utilization of wind energy to move a vessel in the sea water. The sky sails technology allows the towing kite to gain a height of anything between 100 m to 300 m. The sailing kite is made in such a way that it can be raised to its proper elevation and then brought back with the help of a telescopic mast that enables the kite to be raised properly and effectively.
Based on the following figure related to sky sailing answer the questions:
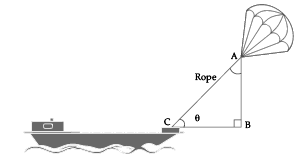
(i) In the given figure, if tan θ = cot (30° + θ), where Q and 30° + θ are acute angles, then the value of θ.
(ii) Find the value of tan 30°. cot 60°.
(i) Given, tan θ = cot(30° + θ)
= tan[90° – (30° + θ)]
= tan(90° – 30° – θ)
⇒ tan θ = tan(60° – θ)
⇒ θ = 60° – θ
⇒ 2θ = 60°
⇒ θ = 30°.
(ii) tan 30° = 1/√3
cot 60° = 1/√3
Now, tan 30° × cot 60° =
= 1/3.
Case Study-2
Q.14. A ladder has rungs 25 cm apart. (see the below).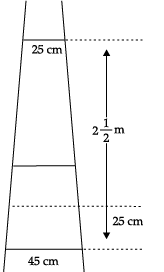
The rungs decrease uniformly in length from 45 cm at the bottom to 25 cm at the top. The top and the bottom rungs are 2(1/2)m apart.
(i) Find the number of the rungs:
(ii) What is the length of the wood required for the rungs?
(i) The distance between the two rungs is 25 cm.
Hence, the total number of rungs
(ii) Here, length of first rung be a and last rung be l, then
Sn = (n/2)(a+l)
Here, a = 25, l = 45
and n = 11
Then, the required length of the wood,
S11 = (11/2)[25 + 45]
= (11/2) x 70
= 385 cm.
|
303 docs|7 tests
|

|
Explore Courses for Class 10 exam
|

|

 To Prove : AP = BP
To Prove : AP = BP










 In ∆PQS, tan60° = y/20
In ∆PQS, tan60° = y/20
 Let PR be the building and AB be the boy
Let PR be the building and AB be the boy





 (Given)
(Given)




















