Electrostatic Potential & Capacitance Class 12 Notes Physics Chapter 2
Many of us have experienced hearing a crackle when we take off our synthetic shirts or nylon sweaters. Sometimes, we also feel the sensation of an electric shock while opening the door of our car. The reason for these experiences is the discharge of electric charges through our body, which accumulate due to rubbing of insulating surfaces. Another common example of electric discharge is the lightning that we see in the sky during thunderstorms.
In this document, we will study in detail about the concepts of electrostatics.
What is Electrostatics?
Electrostatics is a branch of physics that deals with the study of stationary electric charges and their interactions. It focuses on understanding the behavior of electric charges at rest and the forces that arise between them.
 Electrostatic deals with Static Charge
Electrostatic deals with Static Charge
- When you rub a balloon against your hair or a piece of wood, the charged balloon can attract small objects, such as small pieces of paper or hair.
- Similar phenomena occur if we rub a glass rod or an amber rod with a cloth or with a piece of fur.
- Why does this happens?
The answers to all these questions come from a branch of physics known as electromagnetism, thestudy of electric and magnetic interactions. and Electrostatics is the branch of electromagnetics dealing with the effects of electric charges at rest
What is an Electric Charge?
The property associated with matter due to which it produces and experiences electric and magnetic fields is Electric Charge. The SI unit of charge is coulomb (C) and e has the value
e = 1.6 * 10-19C
 Properties of Electric Charges
Properties of Electric Charges
Regarding charge the following points are worth noting:
- Like charges repel each other and unlike charges attract each other.
- Charge is a scalar and can be of two types positive or negative.
- Charge is quantized. The quantum of charge is e. The charge on any body will be some integral
multiple of e, i.e. where, n =1,2,3...
where, n =1,2,3... - During any process, the net electric charge of an isolated system remains constant or we can say that charge is conserved.
- A charged particle at rest produces electric field. A charged particle in an unaccelerated motion produces both electric and magnetic fields but does not radiate energy.
- Unit of Electric Charge
C.G.S., q = ±1 stat-coulomb
S.I., q = ±1 Coulomb - Relation between coulomb and stat-coulomb
1 coulomb = 3×109 stat-coulomb
1 coulomb =(1/10) ab-coulomb (e.m.u of charge)
Q.1. How many electrons are there in one coulomb of negative charge?
Answer: The negative charge is due to the presence of excess electrons, since they carry negative charge. Because an electron has a charge whose magnitude is e = 1.6×10-19C , the number of electrons is equal to the charge q divided by the charge e on each electron. Therefore, the number n of electrons is
Conductors, Insulators, and Semiconductors
- A body in which electric charge can easily flow through is called a conductor (e.g. metals).
- A body in which electric charge cannot flow is called an insulator or dielectric. (e.g. glass, wood, rubber, plastic, etc)
- Substances that are intermediate between conductors and insulators are called semiconductors. (e.g. silicon, germanium, etc)
Charging of a Body
Mainly there are the following three methods of charging a body :
- Conduction
- Induction
- Friction
- Charging a body by conduction: The process of charging by bringing a charged body in contact with a neutral body is called charging by conduction. We observe that both bodies involved in this method of charging by conduction acquire the same type of charge once the process is complete.
 Charging a body by Conduction
Charging a body by Conduction - Charging a body by induction: When a charged object, 'A' is placed near an uncharged object B, object A induces an unlike charge on the near side of B and a like charge on its far side. In this case, the charges inside B are only polarised and no transfer of charges takes place. In this method, we observe that the induced charge is always equal to the inducing charge for a conductor.
 Charging a body by Induction
Charging a body by Induction
- Charging a body by friction: When two uncharged or neutral objects made of different materials, say a glass rod and a silk cloth, are rubbed against each other, both objects get electrified due to a transfer of charges. When rubbed, the glass rod loses a few electrons to the silk cloth. This deficit of electrons on the glass rod makes it positively charged and the excess of electrons makes the silk cloth negatively charged. In this method, there is a transfer of electrons from one body to another. The material that gains electrons is negatively charged and the one that loses electrons is positively charged.
 Charging a body by friction
Charging a body by friction
Q.2. If we comb our hair on a dry day and bring the comb near small pieces of paper, the comb attracts the pieces, why?
Answer: This is an example of frictional electricity and induction. When we comb our hair, it gets positively charged by rubbing. When the comb is brought near the pieces of paper some of the electrons accumulate at the edge of the paper piece which is closer to the comb. At the farther end of the piece there is deficiency of electrons and hence, positive charge appears there. Such a redistribution of charge in a material, due to presence of a nearby charged body is called induction. The comb exerts larger attraction on the negative charges of the paper piece as compared to the repulsion on the positive charge. This is because the negative charges are closer to the comb. Hence, there is a net attraction between the comb and the paper piece.
Coulomb’s Law
Coulomb's Law states that the electrostatic force of attraction or repulsion between two charged bodies is directly proportional to the product of their charges and varies inversely as the square of the distance between the two bodies.
 Coulomb's Law
Coulomb's Law
Mathematically, it can be expressed as:
F = k * (|q1 * q2|) / r2
Where:
- F represents the electrostatic force between the charges.
- q1 and q2 are the magnitudes of the charges of the two objects.
- r is the distance between the charges.
- k is the electrostatic constant, also known as Coulomb's constant.
Where, k = 1/(4πε0) = 9×109 Nm2C-2 (in free space) - quantity ε0 is called the permittivity of free space. It has the value,

Regarding Coulomb's law, the following key points are worth noting:
- Principle of superposition of forces: Coulomb's law describes the interaction between two point charges. When two charges simultaneously exert forces on a third charge, the total force acting on that charge is the vector sum of the forces exerted by the two charges individually. This property is known as the principle of superposition of forces, which holds true for any number of charges.
 Superposition Principle
Superposition Principle
- Action-reaction pair: The electric force between two charges is an action-reaction pair, meaning that the two charges exert equal and opposite forces on each other. This is in accordance with Newton's third law of motion.
- Conservative Force: The electric force is conservative in nature. This implies that the work done by the electric force in moving a charge along any closed path is zero.
- Coulomb's law, as stated above, applies to point charges in a vacuum. However, if there is a dielectric (insulating) material present between the charges, the net force acting on each charge is altered.
The mathematical expression for Coulomb's law can be represented as:
For charges in vacuum:
F = (1 / (4πε₀)) * (q₁ * q₂) / r²
For charges in a medium with dielectric constant K:
F' = (1 / (4πε)) * (q₁ * q₂) / r²
Here, ε₀ is the permittivity of vacuum, and ε is the permittivity of the medium.
Q.3. What is the smallest electric force between two charges placed at a distance of 1.0 m?
Electric Field
When two charged particles are at a distance from each other, they cannot directly interact. However, a charged particle creates an electric field in the space around it. This electric field exerts a force on any other charge placed within it, except for the source charge itself.
 Electric Field
Electric Field
- The electric field refers to the region surrounding a charge or distribution of charges where its electrical effects can be observed. It can be described using either the vector function E, known as electric field strength, or the scalar function V, known as electric potential. The electric field can also be visualized using lines of force.
- Below, we will explore the interrelation between electric field strength E and electric potential V, similar to how acceleration, velocity, and displacement of a particle are related to each other.
1. Electric Field Strength ( )
)
The strength of an electric field is measured by the force experienced by a unit positive charge placed at that point. The direction of the field is given by the direction of motion of a unit positive charge if it were free to move.
 Electric Field Strength Formula
Electric Field Strength Formula
For positive source charge, the electric field is radially outward, whereas, for negative source charge, the electric field is radially inward.
Unit of Electric field
E = [Newton/Coulomb] or [Joule/(Coulomb) (meter)]
An Electric Field Leads to a Force:Suppose there is an electric field strength E at some point in an electric field, then the electrostatic force acting on a charge +q is qE in the direction of E, while on the charge – q it is qE in the opposite direction of E.
Q.4. An electric field of 105 N/C points due west at a certain spot. What are the magnitude and direction of the force that acts on a charge of + 2 μC and − 5 μC at this spot?
Solution:
2. Electric Field Lines of Electric Lines of Force
The strength and direction of the electric field are represented by electric lines of forces or electric field lines.
 Electric Field Lines
Electric Field Lines
- These electric field lines' directions show the flow of electric charge from positive to negative charge.
- These electric field lines which have the same electric field intensity are known as equipotential lines.
- The electric field lines that originate from the positive charge are called positive lines, and the same for the negative charge is known as negative lines.
Characteristics of Electric Field Lines:
- Electric field lines of point charges originate from the positive charge and terminate at the negative charge, indicating the flow of charge from positive to negative.
- Electric field lines have a single direction of flow within a given electric field, as intersecting lines would contradict their behavior.
- Electric field lines are established between charges of opposite polarity, forming attractive force lines.
- Charges with the same polarity repel each other, resulting in the establishment of repulsive force lines along the electric field lines.
Properties of Electric Field Lines:
 Electric Field Lines
Electric Field Lines
- The electric field lines do not intersect each other at any cost. If they do so, it violates the rules of electric field lines.
- The strength of the electric field is maximum where the length of electric field lines is maximum and closer to each other.
- The electric field always moves in a perpendicular direction to the charge.
- The magnitude of the charge in the electric field system is directly proportional to the number of electric field lines.
- The electric field line always originates from the positive charge and terminates on the negative charge.
- If there is a single point charge, then the electric field line will originate or terminate at infinity.
- The electric field lines are equally spaced and parallel in nature in the case of the uniform electric field.
3. Electric Field Due to a Point Charge
- The electric field produced by a point charge q can be obtained in general terms from Coulomb’s law.
First note that the magnitude of the force exerted by the charge q on a test charge qo is then divide this value by qo to obtain the magnitude of the field.
then divide this value by qo to obtain the magnitude of the field. Electric Field Due to Point Charge
Electric Field Due to Point Charge - If q is positive, E is directed away from q. On the other hand, if q is negative, then E is directed towards q. The electric field at a point is a vector quantity.
- Suppose E1 is the field at a point due to a charge q1 and E2 in the field at the same point due to a charge q2 . The resultant field when both the charges are present is E= E1+ E2
Q.5. Two point charges +8q and -2q are located at x = 0 and x = L respectively. The point on x axis at which net electric field is zero due to these charges is-
Solution: By principle of superposition, the Electric field at a point will be the sum of electric field due to the two charges +8q and -2q
∴ 2x - 2L = x
∴ x = +2L
3. Electric Field of a Ring of Charge
A conducting ring of radius R has a total charge q uniformly distributed over its circumference. We are interested in finding the electric field at point P that lies on the axis of the ring at a distance x from its centre.

Formula of Ex (Electric Field of a Ring of Charge)

- Ex = 0 at x = 0, i.e. field is zero at the centre of the ring.
 i.e. when the point P is much farther from the ring, its field is the same as that of a point charge
i.e. when the point P is much farther from the ring, its field is the same as that of a point charge- Ex will be maximum where dEx/dx = 0 Differentiating Ex w.r.t. x and putting it equal to zero we
get x = R/√2 =(Q/4πϵox
=(Q/4πϵox
4. Electric Field of a Line Charge
Positive charge q is distributed uniformly along a line with length 2a, lying along the y-axis between
y = –a and y = +a . We are here interested in finding the electric field at point P on the x-axis.

Formula of Ex (Electric Field of a Line Charge)
 , i.e. if point P is very far from the line charge, the field at P is the same as that of a point charge.
, i.e. if point P is very far from the line charge, the field at P is the same as that of a point charge.- if we make the line of charge longer and longer, adding charge in proportion to the total length so
that λ, the charge per unit length remains constant. In this case, Equation can be written as:

- Due to infinite line of charge:

Electric Potential Energy
Consider an electric field generated by a positive point charge. The direction of the electric field is such that it is radially outwards.
- When a positive test charge is brought closer to the point charge, it will experience repulsion due to electrostatic or Coulomb force.
- Energy is needed to overcome the repulsive force and move the test charge closer to the point charge, which is a source charge. This energy is known as electric potential energy.

- Electric potential energy is a scalar quantity and possesses only magnitude and no direction.
- It is measured in terms of Joules and is denoted by V.
- It has the dimensional formula of ML2T-3A-1.
- There are two key elements on which the electric potential energy of an object depends: Its own electric charge, Its relative position with other electrically charged objects.
1. Electric Potential Energy Formula
Two electric charges, interacting with each other due to their electric field, have the electric potential energy defined as:
U = (k · q1 · q2) / r
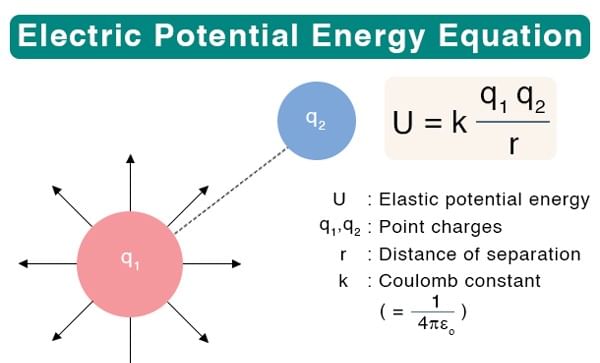
where:
- U [J] – electric potential energy
- k [N·m2/C2] – Coulomb constant
- q1 [C] – electric charge of the first particle
- q2 [C] – mass of second body
- r [m] – distance between the electric charges
The Coulomb constant also known as the electric force constant, or the electrostatic constant, has a fixed value, equal to:
The unit of measurement of electric potential energy is joule [J].
Q.6. Two charges of magnitude 2 nC and 3 nC are placed at 2 cm from each other. Calculate the electric potential energy between these two charges.
Solution:
Given
q1 = 2 nC
q2 = 3 nC
r = 2 cm = 0.02 m
The electric potential energy is given by
U = kq1q2/r
Or, U = (9 x 109 Nm2C-2 x 2 x 10-9 C x 2 x 10-9 C)/0.02 m
Or, U = 2.7 x 10-6J
2.
Electric potential energy of the system having two charges q1 and q2
W = U = 1/(4πε0) (q1q2/r12) = q1V1
Q.7. A particle with the charge of -5 nanocoulombs is at a distance of 10 centimeters away from another charge of 10 nanocoulombs. Calculate the potential energy of the systems form by these two electric charges.
Solution:
Step 1. Convert the electrical charges from [nC] to [C] by multiplying the [nC] value with 10-9:q1 = -5 · 10-9 C
q2 = 10 · 10-9 C
Step 2. Convert the distance from [cm] to [m] by dividing the [cm] value to 100:
r = 10 /100 = 0.1 m
Step 3. Calculate the electric potential energy of the system using equation:
U = (k · q1 · q2) / rU = (8.9875517923 · 109 · (-5) · 10-9 · 10 · 10-9) / 0.1 = – 4.494 · 10-6 J
The resultant electric potential energy is negative, which means that there is an attraction force between the two particles. This is valid since one particle has positive charge and the second particle has negative charge.
3.
Electric potential energy of a three-particle system having charge q1, q2 and q3
W = U = (1/4πε0) (q1q2/r12 + q1q3/r13 + q2q3/r23)
4.
Electric potential energy of a four-particle system having charge q1, q2, q3 and q4
The total energy of this system can be obtained by adding the potential energies of each possible pair.
W = U = (1/4πε0) (q1q2/r12 + q2q3/r23 + q3q4/r34+ q4q1/r41+ q1q3/r13 + q2q4/r24)
5. The electric potential energy of an electric dipole in an electric field
Potential energy of an electric dipole, in an electrostatic field, is defined as the work done in rotating the dipole from zero energy position to the desired position in the electric field.
 If θ = 90º, then W = 0
If θ = 90º, then W = 0- If θ = 0º, then W = -pE
- If θ = 180º, then W = pE
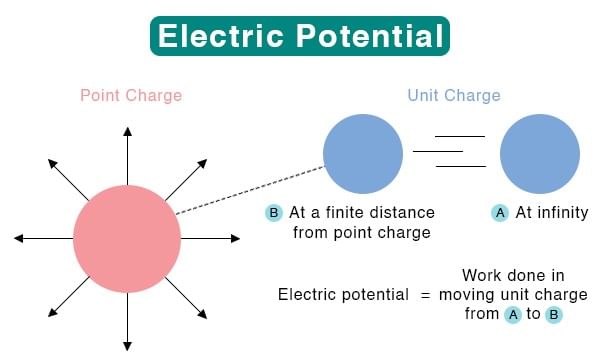
Electric Potential
Electric potential, at any point, is defined as the negative line integral of the electric field from infinity to that point along any path.
The potential difference, between any two points, in an electric field, is defined as the work done in taking a unit positive charge from one point to the other against the electric field.
WAB = q [VA-VB]
So, V = [VA-VB] = W/q
Units & Dimension
- S.I.: V= volt
- C.G.S.: V = stat-volt
- Dimension: [V] = [ML2T-3A-1]
- Relation between volt and stat-volt: 1 volt = (1/300) stat-volt
- Relation between electric field (E) and electric potential (V): E = -dV/dx = -dV/dr
Q.8. A +2 μC test charge is initially at rest a distance of 15 cm from a +7 μC source charge fixed at the origin. The Coulomb force pushes the test charge away from the source charge, reaching 20 cm. What is the work done by the electric field?
Solution:
Given
q1 = +2 μC
q2= +7 μC
rA = 15 cm = 0.15 m
rB = 20 cm = 0.20 m
The work done is given by
W = -ΔV
Or, W = -(kq1q2)(1/rB – 1/rA)
Or, W = -(9 x 109 Nm2C-2 x 7 x 10-6 C x 2 x 10-6 C)(1/0.20 m- 1/0.15 m)
Or, W = 0.21 J
1. Potential due to a point charge
V = (1/4π ε0) (q/r)
2. Potential at a point due to several charges
V = (1/4π ε0) [q1/r1 + q2/r2 + q3/r3] = V1+V2+ V2+….
3. Potential due to charged spherical shell
- Outside, Vout = (1/4π ε0) (q/r)
- Inside, Vin = - (1/4π ε0) (q/R)
- On the surface, Vsurface = (1/4π ε0) (q/R)
4. Potential due to a uniformly charged non-conducting sphere
- Outside, Vout = (1/4π ε0) (q/r)
- Inside, Vin = (1/4π ε0) [q(3R2-r2)/2R3]
- On the surface, Vsurface = (1/4π ε0) (q/R)
- In center, Vcenter = (3/2) [(1/4π ε0) (q/R)] = 3/2 [Vsurface]
5. Common potential (two spheres joined by thin wire):
Common potential, V = (1/4π ε0) [(Q1+Q2)/(r1+r2)]
q1 = r1(Q1+Q2)/(r1+r2) = r1Q/ r1+r2
q2 = r2Q/ r1+r2
q1/q2 = r1/r2 or σ1/ σ2 = r1/r2
6. Potential at any point due to an electric dipole:
V (r,θ) = qa cosθ/(4πε0r2) = p cosθ/(4πε0r2)
- Point lying on the axial line: V = p/4πε0r2
- Point situated on equatorial lines: V = 0
If n drops coalesce to form one drop, then,
- R = n1/3r
- Q = nq
- V = n2/3Vsmall
- σ = n1/3 σsmall
- E = n1/3 Esmall
7. The kinetic energy of a charged particle moving through a potential difference:
K. E = 1/2 mv2 = eV
Electric Dipole & Dipole Moment
An electric dipole is defined as a couple of opposite charges q and –q separated by a distance d.
- By default, the direction of electric dipoles in space is always from negative charge -q to positive charge q.
- The midpoint q and –q is called the centre of the dipole.
- The simplest example of an electric dipole is a pair of electric charges of two opposite signs and equal magnitude separated by distance.
Dipole moment (
) of an electric dipole is defined as the product of the magnitude of one of the charges and the vector distance from negative to positive charge.

Unit of Dipole Moment:
- S.I.: p = coulomb-meter
- C.G.S.: p = stat-coulomb-cm
Electric Potential and Field Due to an Electric Dipole
Consider an electric dipole lying along positive y-direction with its centre at origin.
The electric potential due to this dipole at point A x y z ( , , ) as shown is simply the sum of the potentials due to the two charges. Thus, Electric Potential and Field Due to an Electric DipoleSpecial Cases:
Electric Potential and Field Due to an Electric DipoleSpecial Cases:
1. On the axis of the dipole: 

2. On the perpendicular bisector of dipole


Important Formulaes Related to Electric Dipole & Dipole Moment
As there are too many formulae in electric dipole, we have summarised them as under :
1. | p | = (2a) q
Direction of p is from −q to + q.
2. If a dipole is placed along y-axis with its centre at origin, then
3. On the axis of dipole x = 0, z = 0
4. On the perpendicular bisector of dipole Along x-axis, y = 0, z = 0

5. Dipole in uniform electric field
Problems on Electric Dipole & Dipole Moment
Q.9. Draw electric lines of forces due to an electric dipole.
Solution:
Q.10. Along the axis of a dipole, direction of electric field is always in the direction of electric dipole moment p. Is this statement true or false?
False. In the above figure, we can see that direction of electric field is in the opposite direction of p between the two charges.
Q.11. At a far away distance r along the axis from an electric dipole electric field is E. Find the electric field at distance 2r along the perpendicular bisector.
Gauss’s Law
This law gives a relation between the net electric flux through a closed surface and the charge enclosed by the surface. According to this law, “the net electric flux through any closed surface is equal to the net charge inside the surface divided by ε0 .” In symbols, it can be written as
where, qin represents the net charge inside the closed surface and Erepresents the electric field at any point on the surface.
Simplified Form of Gauss's Theorem
Gauss’s law in simplified form can be written as under:
but this form of Gauss’s law is applicable only under the following two conditions:
(i) The electric field at every point on the surface is either perpendicular or tangential.
(ii) Magnitude of electric field at every point where it is perpendicular to the surface has a constant value (say E).
Applications of Gauss’s Law
As Gauss’s law does not provide expression for electric field but provides only for its flux through a closed surface. To calculate E we choose an imaginary closed surface (called Gaussian surface) in which Simplified Form of Gauss's Theorem can be applied easily. Let us discuss few simple cases.
1. Electric field due to a point charge Electric field due to a point charge
Electric field due to a point charge

2. Electric field due to a linear charge distribution
Let us consider an infinitely long wire with linear charge density λ and length L. To calculate electric field, we assume a cylindrical Gaussian surface. As the electric field E is radial in direction, the flux through the end of the cylindrical surface will be zero.
This is because the electric field and area vector are perpendicular to each other. As the electric field is perpendicular to every point of the curved surface, we can say that its magnitude will be constant.

The surface area of the curved cylindrical surface is 2πrl. The electric flux through the curve is E × 2πrl
According to Gauss’s Law

You need to remember that the direction of the electric field is radially outward if linear charge density is positive. On the other hand, it will be radially inward if the linear charge density is negative.
3. Electric Field due to Infinite Plate Sheet
Let us consider an infinite plane sheet, with surface charge density σ and cross-sectional area A. The position of the infinite plane sheet is as below: The direction of the electric field due to an infinite charge sheet is perpendicular to the plane of the sheet. Let us consider a cylindrical Gaussian surface, whose axis is normal to the plane of the sheet. We can evaluate the electric field E from Gauss’s Law as according to the law:
The direction of the electric field due to an infinite charge sheet is perpendicular to the plane of the sheet. Let us consider a cylindrical Gaussian surface, whose axis is normal to the plane of the sheet. We can evaluate the electric field E from Gauss’s Law as according to the law:
From a continuous charge distribution charge q will be the charge density (σ) times the area (A). Talking about net electric flux, we will consider electric flux only from the two ends of the assumed Gaussian surface. We can attribute it to the fact that the curved surface area and an electric field are normal to each other, thereby producing zero electric flux. So the net electric flux is
Φ = EA – (– EA)
Φ = 2EA
Then, we can write
The term A cancels out which means electric field due to an infinite plane sheet is independent of cross-sectional area A and equals to:
4. Electric Field due to Thin Spherical Shell
Let us consider a thin spherical shell of surface charge density σ and radius “R”. By observation, we can see that the shell has spherical symmetry. Therefore, we can evaluate the electric field due to the spherical shell in two different positions:
- Electric field outside the spherical shell
- Electric field inside the spherical shell
Electric Field Outside the Spherical Shell
To find electric field outside the spherical shell, we take a point P outside the shell at a distance r from the centre of the spherical shell. By symmetry, we take Gaussian spherical surface with radius r and centre O. The Gaussian surface will pass through P, and experience a constant electric field E all around as all points are equally distanced “r’’ from the centre of the sphere. Then, according to Gauss’s Law:
The enclosed charge inside the Gaussian surface q will be σ × 4 πR2. The total electric flux through the Gaussian surface will be
Φ = E × 4 πr2
Then by Gauss’s Law, we can write
Putting the value of surface charge density σ as q/4 πR2, we can rewrite the electric field as
In vector form, the electric field is
where r is the radius vector, depicting the direction of electric field. What we must note here is that if the surface charge density σ is negative, the direction of the electric field will be radially inward.
Electric Field Inside the Spherical Shell
To evaluate electric field inside the spherical shell, let’s take a point P inside the spherical shell. By symmetry, we again take a spherical Gaussian surface passing through P, centered at O and with radius r. Now according to Gauss’s Law
The net electric flux will be E × 4 π r2.
Problems on Gauss Law
Q.12. A uniform electric field of magnitude E = 100 N/C exists in the space in the X-direction. Using the Gauss theorem, calculate the flux of this field through a plane, square area of edge 10 cm placed in the Y-Z plane. Take the normal along the positive X-axis to be positive.
Solution:
The flux Φ = ∫ E.cosθ ds
As the normal to the area points along the electric field, θ = 0
Also, E is uniform so, Φ = E.ΔS = (100 N/C) (0.10m)2 = 1 N-m2
Q.13. A large plane charge sheet having surface charge density σ = 2.0 × 10-6 C-m-2 lies in the X-Y plane. Find the flux of the electric field through a circular area of radius 1 cm lying completely in the region where x, y and z are all positive and with its normal, making an angle of 600 with the Z-axis.
Solution: The electric field near the plane charge sheet is E = σ/2ε0 in the direction away from the sheet. At the given area, the field is along the Z-axis.
The area = πr2 = 3.14 × 1 cm2 = 3.14 × 10-4 m2.
The angle between the normal to the area and the field is 600.
Hence, according to Gauss theorem, the flux
Q.14. A particle of mass 5 × 10-6g is kept over a large horizontal sheet of charge of density 4.0 × 10-6 C/m2 (figure). What charge should be given to this particle so that if released, it does not fall down? How many electrons are to be removed to give this charge? How much mass is decreased due to the removal of these electrons?
Solution:The electric field in front of the sheet is
E = σ/2ε0 = (4.0 × 10-6)/(2 × 8.85 × 10-12) = 2.26 × 105 N/C
If a charge q is given to the particle, the electric force qE acts in the upward direction. It will balance the weight of the particle, if
q × 2.26 × 105 N/C = 5 × 10-9 kg × 9.8 m/s2
or, q = [4.9 × 10-8]/[2.26 × 105]C = 2.21 × 10-13 C
The charge on one electron is 1.6 × 10-19C. The number of electrons to be removed
= [2.21 × 10-13]/[1.6 × 10-19] = 1.4 × 106
Mass decreased due to the removal of these electrons = 1.4 × 106 × 9.1 × 10-31 kg = 1.3 × 10-24 kg.
Electric Field and Potential Due To Charged Spherical Shell or Solid Conducting Sphere
At all points inside the charged spherical conductor or hollow spherical shell, electric field E = 0, as there is no charge inside such a sphere.
Electric Field: 
Potential:
Electric Field and Potential Due to a Solid Sphere of Charge

Electric Field:

Potential:
Capacitance
The capacitance of a conductor is defined as the ratio between the charge of the conductor to its potential.
C = Q/V
Units & Dimension
- S.I.: C = farad (coulomb/volt)
- C.G.S.: C = stat-farad (stat-coulomb/stat-volt)
- Dimension: [M-1L-2T4A2]
The capacity of an isolated spherical conductor:
C = 4πε0r
Capacitor: A capacitor or a condenser is an arrangement that provides a larger capacity in a smaller space.
The capacity of a parallel plate capacitor:
Cair = ε0A/d
Cmed = Kε0A/d
Here, A is the common area of the two plates and d is the distance between the plates.
Effect of dielectric on the capacitance of a capacitor:
C = ε0A/[d-t+(t/K)]
Here d is the separation between the plates, t is the thickness of the dielectric slab, A is the area and K is the dielectric constant of the material of the slab.
If the space is completely filled with dielectric medium (t=d), then, C = ε0KA/ d
The capacitance of a sphere:
- Cair = 4πε0R
- Cmed = K (4πε0R)
The capacity of a spherical condenser:
- When outer sphere is earthed:
Cair = 4πε0 [ab/(b-a)]
Cmed = 4πε0 [Kab/(b-a)] - When the inner sphere is earthed:
C1= 4πε0 [ab/(b-a)]
C2 = 4πε0b
Net Capacity, C '=4πε0[b2/b-a]
Increase in capacity, ΔC = 4π ε0b
It signifies, by connecting the inner sphere to earth and charging the outer one we get an additional capacity equal to the capacity of the outer sphere.
The capacity of a cylindrical condenser:
- Cair = λl / [(λ/2π ε0) (loge b/a)] = [2πε0l /(loge b/a) ]
- Cmed = [2πKε0l /(loge b/a) ]
The potential energy of a charged capacitor (Energy stored in a capacitor)
W = ½ QV = ½ Q2/C = ½ CV2
The energy density of a capacitor:
U = ½ ε0E2 = ½ (σ2/ ε0)
This signifies the energy density of a capacitor is independent of the area of plates and the distance between them so, the value of E does not change.
Grouping of Capacitors
Capacitors in parallel:
- C = C1+C2+C3+…..+Cn
The resultant capacity of a number of capacitors, connected in parallel, is equal to the sum of their individual capacities.
- V1= V2= V3 = V
- q1 =C1V, q2 = C2V, q3 = C3V
- Energy Stored, U = U1+U2+U3
Capacitors in series:
- 1/C = 1/C1 + 1/ C2 +……+ 1/Cn
- The reciprocal of the resultant capacity of a number of capacitors, connected in series, is equal to the sum of the reciprocals of their individual capacities.

- q1 = q2 = q3 = q
- V1= q/C1, V2= q/C2, V3= q/C3
- Energy Stored, U = U1+U2+U3
Energy stored in a group of capacitors:
- Energy stored in a series combination of capacitors:
W = ½ (q2/C1) + ½ (q2/C2) + ½ (q2/C3) = W1+W2+W3
Thus, net energy stored in the combination is equal to the sum of the energies stored in the component capacitors. - Energy stored in a parallel combination of capacitors:
W = ½ C1V2 +½ C2V2 + ½ C3V2 = W1+W2+W3
The net energy stored in the combination is equal to the sum of energies stored in the component capacitors.
Force of attraction between plates of a charged capacitor:
(a) F = ½ ε0E2A
(b) F = σ2A/2ε0
(c) F=Q2/2ε0A
Force on a dielectric in a capacitor:
F = (Q2/2C2) (dC/dx) = ½ V2 (dC/dx)
Common potential when two capacitors are connected
V = [C1V1+ C2V2] / [C1+C2] = [Q1+Q2]/ [C1+C2]
Charge transfer when two capacitors are connected
ΔQ = [C1C2/C1+C2] [V1-V2]
Energy loss when two capacitors are connected
ΔU = ½ [C1C2/C1+C2] [V1-V2] 2
Charging of a capacitor
- Q = Q0(1-e-t/RC)
- V = V0(1-e-t/RC)
- I = I0(1-e-t/RC)
- I0 = V0/R
Discharging of a capacitor
- Q = Q0(e-t/RC)
- V = V0(e-t/RC)
- I = I0(e-t/RC)
Time constant

Some Additional Formulas and Terms
1. Electric Field due to Uniformly Charged Disc:
At a point on its axis, E = (1/4πε0)(2πσ)[1 - x/(a2+R2)1/2] Here, σ is the surface charge.
2. Electric field due to thin spherical shell:

- Outside Point: Eout = (1/4πε0) (q/r2)
- Inside Point: Ein = 0
3. E
lectric field of a spherically symmetric distribution of charge of Radius R:

3. E
- Point at outside (r > R): E = (1/4πε0) (q/r2)
- Point at inside (r < R): E = (1/4πε0) (qr/R3)
Here, q is the total charge.
4. Electric field of a non-conducting solid sphere having uniform volume distribution of charge:

- Outside Point: Eout = (1/4πε0) (Q/r2)
- Inside Point: Ein = (1/4πε0) (Qr/R3)
- On the Surface: Esurface = (1/4πε0) (Q/R2)
Here, Q is the total charge
5. The electric field of a cylindrical conductor of infinite length having line charge λ:
- Outside the cylinder: E = λ/(2πε0r)
- Inside the cylinder: E = 0
6. The electric field of a non-conducting cylinder having uniform volume density of charge:
- Outside the cylinder: E = λ/2πε0r
- Inside the cylinder: E = ρr/2ε0
7. The electric field of an infinite plane sheet of charge surface charge (σ):
E = σ/2ε0

8. Electric field due to two oppositely infinite charged sheets:

- Electric field at points outside the charged sheets: EP = ER = 0
- Electric field at a point in between the charged sheets: EQ = σ/ε0
9. Electric field due to an infinite non-conducting flat sheet having charge σ:
E = σ/2ε0
This signifies, the electric field near a charged sheet is independent of the distance of the point from the sheet and depends only upon its charge density and is directed normally to the sheet.
10. Electric field due to an infinite flat conductor carrying charge:
E= σ/ε0
11. Electric pressure (Pelec) on a charged conductor:
Pelec = (1/2 ε0) σ2
|
357 docs|148 tests
|
FAQs on Electrostatic Potential & Capacitance Class 12 Notes Physics Chapter 2
| 1. What is Electrostatics? |  |
| 2. What is an Electric Charge? |  |
| 3. What is Coulomb's Law? |  |
| 4. What is Electric Potential? |  |
| 5. What is Gauss's Law? |  |


 where, n =1,2,3...
where, n =1,2,3...





 )
)

 then divide this value by qo to obtain the magnitude of the field.
then divide this value by qo to obtain the magnitude of the field.

 i.e. when the point P is much farther from the ring, its field is the same as that of a point charge
i.e. when the point P is much farther from the ring, its field is the same as that of a point charge
 , i.e. if point P is very far from the line charge, the field at P is the same as that of a point charge.
, i.e. if point P is very far from the line charge, the field at P is the same as that of a point charge.
 If θ = 90º, then W = 0
If θ = 90º, then W = 0 ) of an electric dipole is defined as the product of the magnitude of one of the charges and the vector distance from negative to positive charge.
) of an electric dipole is defined as the product of the magnitude of one of the charges and the vector distance from negative to positive charge.


























