Electrical Engineering (EE) Exam > Electrical Engineering (EE) Notes > Signals and Systems > Study Notes For Z-Transform
Study Notes For Z-Transform | Signals and Systems - Electrical Engineering (EE) PDF Download
Z-Transform
- Computation of the Z-transform for discrete-time signals.
- Enables analysis of the signal in the frequency domain.
- Z-Transform takes the form of a polynomial.
- Enables interpretation of the signal in terms of the roots of the polynomial.
- z−1 corresponds to a delay of one unit in the signal.
The Z - Transform of a discrete time signal x[n] is defined as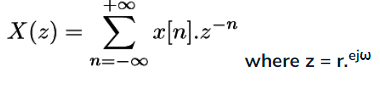
- The discrete-time Fourier Transform (DTFT) is obtained by evaluating Z-Transform at z = ejω.
- The z-transform defined above has both sided summation. It is called bilateral or both sided Z-transform.
Unilateral (one-sided) z-transform
- The unilateral z-transform of a sequence x[n] is defined as
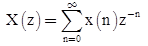
Region of Convergence (ROC):
ROC is the region where z-transform converges. It is clear that z-transform is an infinite power series. The series is not convergent for all values of z.
Significance of ROC
- ROC gives an idea about values of z for which z-transform can be calculated.
- ROC can be used to determine causality of the system.
- ROC can be used to determine stability of the system.
Summary of ROC of Discrete Time Signals for the sequences

Characteristic Families of Signals and Corresponding ROC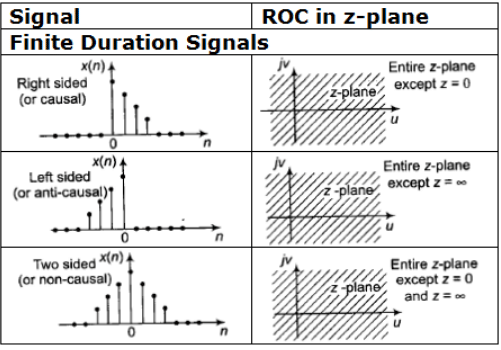
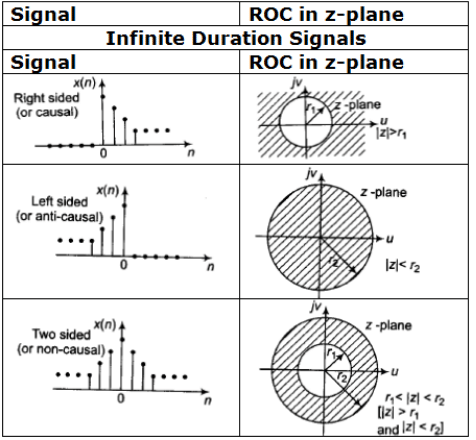
Note: X(z) = z{x(n)} ; X1 (z) = Z {xl (n)} ; X2(z) = z{x2 (n)}; Y(z) = z (y (n))
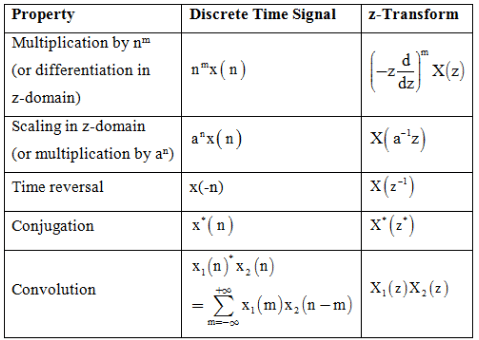
Summary of Properties of z- Transform: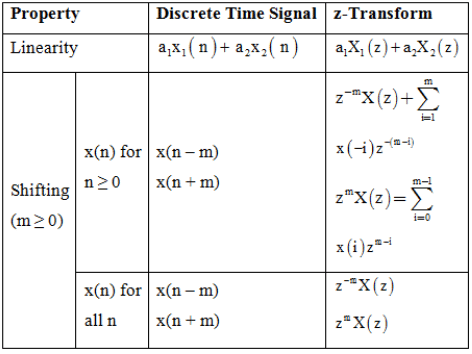

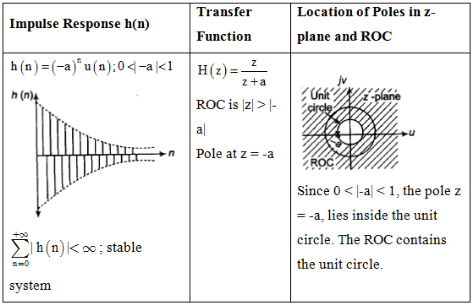
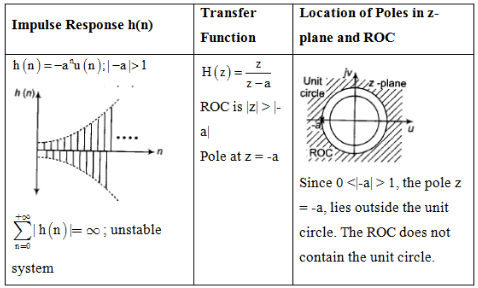
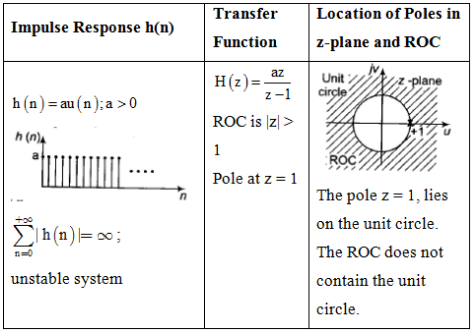
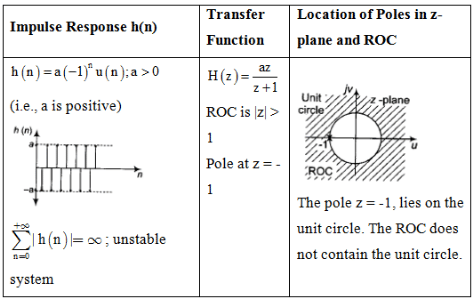
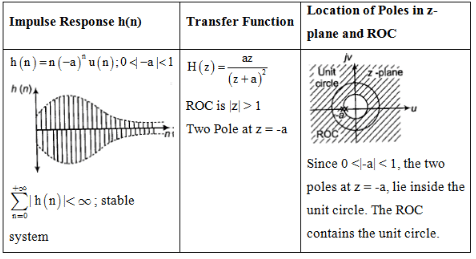
Impulse Response and Location of Poles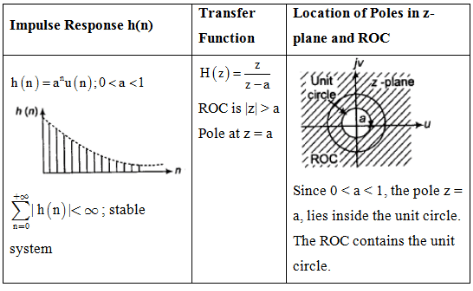


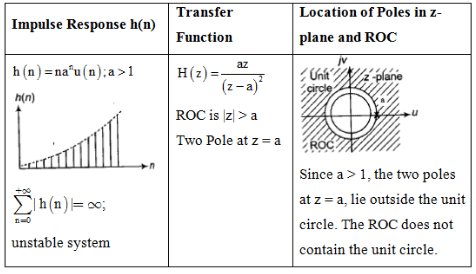
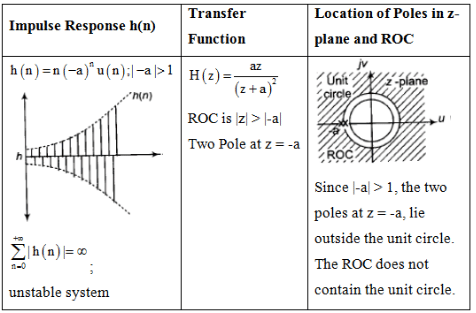
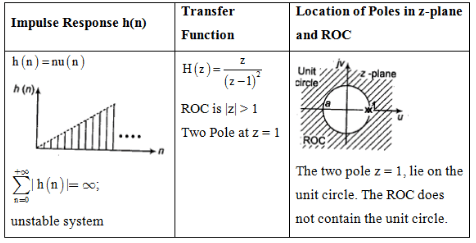
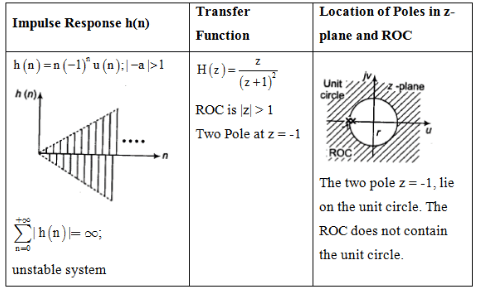

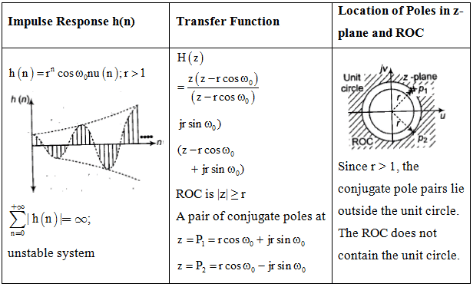

The document Study Notes For Z-Transform | Signals and Systems - Electrical Engineering (EE) is a part of the Electrical Engineering (EE) Course Signals and Systems.
All you need of Electrical Engineering (EE) at this link: Electrical Engineering (EE)
|
45 videos|70 docs|33 tests
|
FAQs on Study Notes For Z-Transform - Signals and Systems - Electrical Engineering (EE)
| 1. What is the Z-transform and why is it important? |  |
Ans. The Z-transform is a mathematical transform used in digital signal processing to convert discrete time-domain signals into complex frequency-domain representations. It is important because it allows us to analyze the behavior of discrete systems in the frequency domain, which is crucial for designing and understanding digital filters and control systems.
| 2. How is the Z-transform different from the Fourier transform? |  |
Ans. The Z-transform and the Fourier transform are both used for analyzing signals in the frequency domain. However, the Z-transform is specifically designed for discrete-time signals, while the Fourier transform is used for continuous-time signals. The Z-transform can handle both causal and non-causal signals, while the Fourier transform assumes causality. Additionally, the Z-transform provides information about the system's behavior over the entire complex plane, whereas the Fourier transform only provides information about the system's behavior on the unit circle.
| 3. What is the region of convergence (ROC) in the Z-transform? |  |
Ans. The region of convergence (ROC) in the Z-transform is a set of values in the complex plane for which the Z-transform converges and the resulting series or integral is finite. It is important to determine the ROC because it indicates the range of values for which the Z-transform is valid. The ROC can be inside or outside the unit circle, or it can be a combination of both.
| 4. How do you calculate the inverse Z-transform? |  |
Ans. To calculate the inverse Z-transform, you need to find the original time-domain sequence from its Z-transform representation. This can be done using techniques such as partial fraction expansion, power series expansion, or contour integration. The method used depends on the complexity of the Z-transform and the properties of the sequence. The inverse Z-transform allows us to obtain the time-domain representation of a system from its frequency-domain representation.
| 5. What are some practical applications of the Z-transform? |  |
Ans. The Z-transform has various practical applications in digital signal processing and control systems. Some examples include:
- Digital filter design: The Z-transform is used to design and analyze digital filters, which are essential for processing and manipulating digital signals.
- System analysis and stability: The Z-transform helps analyze the stability and behavior of discrete-time systems, such as control systems and communication systems.
- Time series analysis: The Z-transform is used to analyze and model time series data, which is common in fields such as finance, economics, and meteorology.
- Image and audio processing: The Z-transform is used in image and audio processing algorithms to perform various operations, such as compression, filtering, and enhancement.
- Digital communication: The Z-transform is used in modulation and demodulation techniques for digital communication systems, allowing efficient transmission and reception of digital signals.
Related Searches





















