Class 10 Mathematics: CBSE Sample Question Paper- Term II (2021-22) - 1 | CBSE Sample Papers For Class 10 PDF Download
| Table of contents |

|
| Class-X |

|
| Time: 120 |

|
| Minutes |

|
| M.M: 40 |

|
| Section - A |

|
| Section - B |

|
| Section - C |

|
Class-X
Time: 120
Minutes
M.M: 40
General Instructions:
Read the following instructions very carefully and strictly follow them:
- The question paper consists of 14 questions divided into 3 sections A, B, C.
- All questions are compulsory.
- Section A comprises of 6 questions of 2 marks each. Internal choice has been provided in two questions.
- Section B comprises of 4 questions of 3 marks each. Internal choice has been provided in one question.
- Section C comprises of 4 questions of 4 marks each. An internal choice has been provided in one question. It contains two case study based questions.
Section - A
Q.1. Find the 20th term from the last term of the A.P.: 3, 8, 13, ...... 253.
OR
If 7 times the 7th term of an A.P. is equal to 11 times its 11th term, then find its 18th term.
20th term from the end = l – (n – 1)d
= 253 – 19 × 5
= 158
Detailed Solution:
Given, A.P.: 3, 8, 13, .......... 253
Here, first term (a) = 3, common difference (d) = 8 – 3 = 5 and last term (l) = 253
Then, 20th term from the end of the A.P.
= l – (n – 1)d
= 253 – (20 – 1)5
= 253 – 95
= 158.
OR
7a7 = 11a11
⇒ 7(a + 6d) = 11(a + 10d)⇒ a + 17d = 0
∴ a18 = 0
Detailed Solution:
Given, 7a7 = 11a11
∵ an = a + (n – 1)d
Then, 7[a + (7 – 1)d] = 11[a + (11 – 1)d]
⇒ 7(a + 6d) = 11(a + 10d)
⇒ 7a + 42d = 11a + 110 d
⇒ 11a – 7a = 42d – 110d
⇒ 4a = – 68d
⇒ a = – 17d
⇒ a + 17d = 0
i.e., a + (18 – 1)d = 0
Hence, a18 = 0.
Q.2. A fast train takes 3 hours less than a slow train for a journey of 600 km. If the speed of the slow train is 10 km/h less than that of the fast train, find the speed of each train.
Total distance of the journey = 600 km
Let speed of fast train = x km/h,
then speed of slow train = (x – 10) km/h
According to question,
⇒
⇒
⇒ x2 – 10x – 2000 = 0
⇒ x2 – 50x + 40x – 2000 = 0
⇒ x(x – 50) + 40(x – 50) = 0
⇒ (x – 50)(x + 40) = 0
Either, x = 50 or x = – 40
∵ speed can not be negative.
So, the speed of fast train = 50 km/h, and the speed of slow train = 50 – 10 = 40 km/h.
Q.3. In the given figure PQ is chord of length 6 cm of the circle of radius 6 cm. TP and TQ are tangents to the circle at points P and Q respectively. Find ∠PTQ.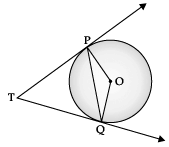
Here, PQ = 6 cm, OP = OQ = 6 cm (radii)
∴ PQ = OP = OQ
∴ ∠POQ = 60°
(angle of equilateral ∆)
∠OPT = ∠OQT = 90° (radius ⊥ tangent)∴ ∠PTQ + 90° + 90° + 60° = 360°
(angle sum property)
∠PTQ = 120°.
Q.4. A well of diameter 4 m dug 21 m deep. The earth taken out of it has been spread evenly all around it in the shape of a circular ring of width 3 m to form an embankment. Find the height of the embankment.
Diameter of well = 4 m
Radius of well, r = 2 m
Depth of well, h = 21 m,
Volume of earth dug out = πr2h
= (22/7) x 2 x 2 x 21 = 264m3
Width of embankment = 3 m
Outer radius of ring = 2 + 3 = 5 m
Let the height of embankment be h
∴ Volume of embankment = Volume of earth dug out
π(R2 – r2)h = 264
(22/7) x (25 - 4) x h = 264
h = (264 x 7)/(22 x 21)
∴ Height of embankment = 4 m.
Q.5. Find the mode of the following frequency distribution:
Modal class is 30 – 40
∴ Mode = l +
= 36.
Detailed Solution:
Modal-class = 30 – 40
⇒ l = 30, f0 = 10, f1 = 16, f2 = 12, h = 10
Mode = l +
= 30 +
= 30 + (6/10) x 10
= 30 + 6
= 36.
Q.6. For what values of k, the roots of the equation x2 + 4x + k = 0 are real ?
OR
Find the nature of roots of the quadratic equation 2x2 – 4x + 3 = 0.
Since roots of the equation x2 + 4x + k = 0 are real
⇒ 16 – 4k ≥ 0
⇒ k ≤ 4
Detailed Solution:
Given x2 + 4x + k = 0.
Comparing the given equation with
ax2 + bx + c = 0,
we get a = 1, b = 4, c = k
Since, given the equation has real roots
⇒ D ≥ 0
⇒ b2 – 4ac ≥ 0
⇒ 42 – 4 × 1 × k ≥ 0
⇒ 4k ≤ 16
⇒ k ≤ 4
OR
Given: 2x2 – 4x + 3 = 0
On comparing above with ax2 + bx + c = 0,
we get, a = 2, b = -4, c = 3
Now, D = b2 - 4ac
So, D = (-4)2 - 4(2) × (3)
= -8 < 0 or (-ve)
Hence, the given equation has no real roots.
Section - B
Q.7 The marks obtained by 100 students in an examination are given below :

Find the median marks of the students.
N/2 = 110/2 = 55
The 55th term lies in class 40 – 45.
∴ l = 40, h = 5, f = 28; N/2, = 55, c.f. = 30.
We know,
Since, Median = l +
= 40 + (25/28) x 5
= 40 + 4.46 = 44.46 (Approx)
Q.8. Draw a circle of radius 2 cm with centre O and take a point P outside the circle such that OP = 6.5 cm. From P, draw two tangents to the circle.
Steps of construction :
(i) Draw a line segment OP = 6.5 cm.
(ii) Taking O as centre and radius 2 cm, draw a circle.
(iii) Draw perpendicular bisector of OP, intersect at OP at S.
(iv) Taking S as centre draw another circle which intersects the first circle at Q and R.
(v) Join P to Q and P to R.
Hence PQ and PR are two tangents.
Q.9. Find the mode of the following distribution of marks obtained by the students in an examination :
Given the mean of the above distribution is 53, using empirical relationship estimate the value of its median.
Modal class = 60 – 80
∴ Mode =
Here, l = 60, f1 = 29, f0 = 21, f2 = 17 and h = 20
Mode =
= 60 +x 20
= 60 + 8 = 68
Empirical relationship,
Mode = 3 median – 2 mean
Mode = 68 and mean = 53 (given)
∴ 3 Median = Mode + 2 Mean
3 Median = 68 + 2 × 53
Median = 174/3 = 58
Hence, Median = 58.
Q.10. A man on the top of a vertical observation tower observes a car moving at uniform speed coming directly towards it. If it takes 12 minutes for the angle of depression to change from 30° to 45°, how long will the car take to reach the observation tower from this point ?
OR
The angle of elevation of the top of a hill from the foot of a tower is 60° and the angle of depression from the top of the tower of the foot of the hill is 30°. If tower is 50 metre high, find the height of the hill.
Let the speed of car by x m/minute
In ΔABC, ∠B = 90°
h/y = tan 45°
⇒ h = y ...(i)
In ΔABD, ∠B = 90°
h/(y+12x) = tan 30°
⇒ h√3 = y + 12xy√3 – y = 12x
⇒ y = 6x (√3 +1) ...(ii)
Hence, time taken from C to B = 6 (√3 +1) minutes.OR
Let AB = 50 m be the height of the tower and CD be the height of hill.
Now, in ΔABC,
∠ABC = 90°tan 30° = AB/BC
or,
or, BC = 50√3 m
Again in ΔBCD, ∠BCD = 90°
tan 60° = DC/BC
or, DC = BC tan 60°
= 50√3 ×√3 m
⇒ DC = 150 m
∴ The height of hill is 150 m.
Section - C
Q.11. The internal and external radii of a spherical shell are 3 cm and 5 cm respectively. It is melted and recast into a solid cylinder of diameter 14 cm, find the height of the cylinder. Also find the total surface area of the cylinder. (Take π= 22/7)
Volume of shell = Volume of cylinder
⇒ 4π/3 [53 −33] = π(7)2h
⇒ h = 8/3 = 2(2/3)cm
TSA of cylinder is = 2pr(r + h)
= 2 x (22/7) x 7 x (7 + (8/3))
= 44 x (29/3)
= (1276/3) cm2 or 425.33 cm2
Detailed Solution:
Internal radius (r) = 3 cm
External radius (R) = 5 cm
Radius of cylinder (R1) = 14/2 = 7cm
Let height of cylinder = h cm
According to the question, [When one shape is reshaped into another shape the volumes are same of both shapes]
(4/3) π(R3 – r3) = π(R1)2h
(4/3) π(53 – 33) = (7)2h
(4/3) x (125 – 27) = 49h
h = 8/3 m or 2(2/3) cm
TSA of cylinder = 2πr (h + R1)
= 2 x (22/7) x 7 ((8/3) + 7)
= 44 x (29/3)
= 1276/3 cm2
or 425.33 cm2
Q.12. Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segment joining the points of contact to the centre.
OR
Two tangents TP and TQ are drawn to a circle with centre O from an external point T.
Prove that ∠PTQ = 2∠OPQ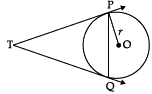
∠OAP + ∠OBP + ∠APB + ∠AOB = 360°
⇒ 90° + 90° + ∠APB + ∠AOB = 360° (∵ Tangent ⊥ radius)
⇒ ∠APB + ∠AOB = 180°Let ∠PTQ = θ
TPQ is an isosceles triangle
∠TPQ = ∠TQP = 1/2 (180° – θ)
= 900 - (θ/2)
∠OPT = 90°
∠OPQ = ∠OPT – ∠TPQ
= 90°− (900 - (θ/2))
= (θ/2)
∠OPQ = 1/2 ∠PTQ
2∠OPQ = ∠PTQ
Detailed Solution:Given: PA and PB are two tangents to a circle with centre O.
To Prove:
∠APB + ∠AOB = 180°
Proof:is a quadrilateral, OA is radius and PA & PB are tangents.
∴ ∠OAP = ∠OBP = 90°
[Radius is always perpendicular to tangent]
By angle sum property of quadrilateral.
∴ ∠AOB + ∠OBP + ∠APB + ∠OAP = 360°
∠AOB + 90° + ∠APB + 90° = 360°
∴ ∠APB + ∠AOB = 180° Hence Proved.
OR
Given: A circle with centre O two tangents TP and TQ to the circle where P and Q are the point of contact.
To Prove: ∠PTQ = 2∠OPQ
Proof: TP = TQ
[length of tangents drawn from same external point to a circle are equal]∴ ∠TQP = ∠TPQ ...(i)
[Angles opposite to equal sides are equal]
Now, PT is a tangent & OP is radius
∴ OP ⊥ TP [Radius and Tangent are perpendicular to each other]
⇒ ∠OPT = 90°
∠OPQ + ∠TPQ = 90°
∠TPQ = 90° – ∠OPQ ...(ii)
In ∆PTQ,
By angle sum property of triangle, ∠TPQ + ∠TQP + ∠PTQ = 180° [From (i)]
∠TPQ + ∠TPQ + ∠PTQ = 180°
⇒ 2[TPQ + ∠PTQ = 180°
⇒ 2(90° – ∠OPQ) + ∠PTQ = 180° [From (ii)]
⇒ 180 – 2∠OPQ + ∠PTQ = 180°
∠PTQ = 2∠OPQ Hence Proved.
Case Study-1
Q.13. Trigonometry in the form of triangulation forms the basis of navigation, whether it is by land, sea or air. GPS a radio navigation system helps to locate our position on earth with the help of satellites.
A guard, stationed at the top of a 240 m tower, observed an unidentified boat coming towards it. A clinometer or inclinometer is an instrument used for measuring angles or slopes(tilt). The guard used the clinometer to measure the angle of depression of the boat coming towards the lighthouse and found it to be 30°. (Lighthouse of Mumbai Harbour. Picture credits - Times of India Travel)
(Lighthouse of Mumbai Harbour. Picture credits - Times of India Travel)
(i) Make a labelled figure on the basis of the given information and calculate the distance of the boat from the foot of the observation tower.
(ii) After 10 minutes, the guard observed that the boat was approaching the tower and its distance from tower is reduced by 240(√3 – 1) m. He immediately raised the alarm. What was the new angle of depression of the boat from the top of the observation tower?
(i)
In ∆PTR, tan 30° = 240/x ⇒ x = 240√3m
(ii) Distance of boat from tower
= 240√3 − 240(√3−1)
= 240 m
Let the angle of depression = θ
tanθ = 240/240 = 1
⇒ θ = 45°
Detailed Solution:(i) Height of light house = 240 m
In ∆PRT, ∠R = 90°
tan 30° = 240/x
x = 240√3 m.
Distance of foot from the foot of observation tower = 240√3 m.
(ii) After 10 minutes,
Distance between boat and light house is reduced by = 24 (√3 −1) m∴ Distance between boat and light house
= 240√3 – 240 (√3 −1)
= 240√3 – 240√3 + 240
= 240 m
Let the point C is the new position of boat,
⇒ θ = 45°
Case Study-2
Q.14. Push-ups are a fast and effective exercise for building strength. These are helpful in almost all sports including athletics. While the push-up primarily targets the muscles of the chest, arms, and shoulders, support required from other muscles helps in toning up the whole body.
Nitesh wants to participate in the push-up challenge. He can currently make 3000 push-ups in one hour. But he wants to achieve a target of 3900 push-ups in 1 hour for which he practices regularly. With each day of practice, he is able to make 5 more push-ups in one hour as compared to the previous day. If on first day of practice he makes 3000 push-ups and continues to practice regularly till his target is achieved. Keeping the above situation in mind answer the following questions:
(i) Form an A.P representing the number of push-ups per day and hence find the minimum number of days he needs to practice before the day his goal is accomplished?
(ii) Find the total number of push-ups performed by Nitesh up to the day his goal is achieved.
(i) 3000, 3005, 3010, ..., 3900
an = a + (n – 1)d
3900 = 3000 + (n – 1)5
⇒ 900 = 5n – 5 ⇒ 5n = 905⇒ n = 181
Minimum number of days of practice = n – 1
= 180 days(ii) Sn = (n/2) (a+1)
= (181/2) x (3000+ 3900)
= 624450 push-ups
Detailed Solution:
(i) By the given situation the A.P. to be formed is:
3000, 3005, 3010, ...... 3900
First term = a = 3000
Common Difference = d = 3005 – 3000
d = 5
According to the problem
nth term (an) = 3900
To Find n
nth term = an
= a + (n – 1)d
3900 = 3000 + (n – 1)5
3900 – 3000 = (n – 1)5
900 = (n – 1)5
900/5 = n - 1
180 + 1 = n
or n = 181
Minimum number of days he needs to practice before his goal is accomplished
= 181 – 1 [Excluding the last day]
= 180
(ii) Total Number of push-ups performed means sum of all push-ups he did in 181 days.
∴ Sn = n/2[a + l] ...(i)
Sn = Sum of all push-ups in 181 days.
n = number of days = 181
a = first term of the A.P.
= 3000
l = last term = 3900
Put all values in (i)⇒ Sn = (181/2) [3000 + 3900]
= (181/2)[6900]
= 624450
Total number of Push-ups performed in 181 days = 624450.
|
303 docs|7 tests
|
FAQs on Class 10 Mathematics: CBSE Sample Question Paper- Term II (2021-22) - 1 - CBSE Sample Papers For Class 10
| 1. What is the duration of Class 10 Mathematics exam? |  |
| 2. What is the maximum marks for Class 10 Mathematics exam? |  |
| 3. How many sections are there in the Class 10 Mathematics exam? |  |
| 4. Is the Class 10 Mathematics exam conducted in the same language as the article title? |  |
| 5. Are there any sample question papers available for the Class 10 Mathematics exam? |  |

|
Explore Courses for Class 10 exam
|

|




 ∴ ∠PTQ + 90° + 90° + 60° = 360°
∴ ∠PTQ + 90° + 90° + 60° = 360°











 x 20
x 20




 ∠OAP + ∠OBP + ∠APB + ∠AOB = 360°
∠OAP + ∠OBP + ∠APB + ∠AOB = 360°
 Given: PA and PB are two tangents to a circle with centre O.
Given: PA and PB are two tangents to a circle with centre O. is a quadrilateral, OA is radius and PA & PB are tangents.
is a quadrilateral, OA is radius and PA & PB are tangents.























