RS Aggarwal Solutions: Real Numbers - 1 | Mathematics (Maths) Class 10 PDF Download
Q.1. What do you mean by Euclid's division lemma?
Solution: For any two given positive integers a and b there exist unique whole numbers q and r such that
a = bq + r, when 0 ≤ r < b.
Here, we call 'a' as dividend, b as divisor, q as quotient and r as remainder.
Dividend = (Divisor × Quotient) + Remainder
Q.2. A number when divided by 61 gives 27 as quotient and 32 as remainder. Find the number.
Solution: Using Euclid’s divison Lemma
Dividend = (Divisor × Quotient) + Remainder
= (61 × 27) + 32
= 1647 + 32
= 1679
Required number = 1679
Q.3. By what number should 1365 be divided to get 31 as quotient and 32 as remainder?
Solution: By Euclid's Division Algorithm, we have:
Dividend = (Divisor X Quotient) + Remainder
1365 = (Divisor × 31) + 32
(1365 - 32) / 31 = Divisor
⇒ 1333 / 31 = Divisor
Therefore, Divisor = 43
Q.4. Using Euclid's algorithm, find the HCF of:
(i) 405 and 2520
(ii) 504 and 1188
(iii) 960 and 1575
Solution:
(i) On dividing 2520 by 405, we get
Quotient = 6, remainder = 90
Therefore, 2520 = (405 × 6) + 90
Dividing 405 by 90, we get
Quotient = 4,
Remainder = 45
Therefore, 405 = 90 × 4 + 45
Dividing 90 by 45
Quotient = 2, remainder = 0
Therefore, 90 = 45 × 2
H.C.F. of 405 and 2520 is 45
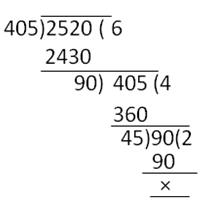
(ii) Dividing 1188 by 504, we get
Quotient = 2, remainder = 180
Therefore, 1188 = 504 × 2 + 180
Dividing 504 by 180
Quotient = 2, remainder = 144
Therefore, 504 = 180 × 2 + 144
Dividing 180 by 144, we get
Quotient = 1, remainder = 36
Dividing 144 by 36
Quotient = 4, remainder = 0
Therefore, H.C.F. of 1188 and 504 is 36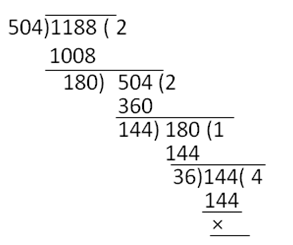
(iii) Dividing 1575 by 960, we get
Quotient = 1, remainder = 615
1575 = 960 x 1 + 615
Dividing 960 by 615, we get Quotient = 1, remainder = 345
960 = 615 x 1 + 345
Dividing 615 by 345 Quotient = 1, remainder = 270
615 = 345 x 1 + 270
Dividing 345 by 270, we get Quotient = 1, remainder = 75
345 = 270 x 1 + 75
Dividing 270 by 75, we get Quotient = 3, remainder =45
270 = 75 x 3 + 45
Dividing 75 by 45, we get Quotient = 1, remainder = 30
75 = 45 x 1 + 30
Dividing 45 by 30, we get Remainder = 15, quotient = 1
45 = 30 x 1 + 15
Dividing 30 by 15, we get Quotient = 2, remainder = 0
H.C.F. of 1575 and 960 is 15 
Q.5. Show that every positive integer is either even or odd.
Solution: Let a be a given positive integer.
On dividing a by 2, let q be the quotient and r be the remainder.
Then, by Eudid's algorithm, we have
a = 2q+ r, where 0 < r < 2
⇒ a = 2q + r, where r = 0,1
⇒ a = 2q or a = 2q + 1
When a = 2q for some integer q, then clearly a is even.
When a = 2q + 1 for some integer q, then dearly a is odd.
Thus, every positive integer is either even or odd.
Q.6. Show that any positive odd integer is of the form (6m + 1) or (6m + 3) or (6m + 5), where m is some integer.
Solution: Let a be a given positive integer.
On dividing a by 6, let q be the quotient and r be the remainder.
Then, by Eudid's algorithm, we have
a = 6q + r, where 0 < r < 6
⇒ a = 6q + r, where r = 0,1,2,3,4,5,6
⇒ a = 6q or a = 6q + 1 or a = 6q + 2 or a = 6q + 3 or a = 6q + 4 or a = 6q + 5
But, a = 6q, a = 6q + 2, a = 6q + 4 gives even values of a.
Thus, when a is odd, it is of the form
6q + 1, 6q + 3 or 6q + 5 for some integer q.
Q.7. Show that any positive odd integer is of the form (4m + 1) or (4m + 3), where in is some integer.
Solution:
Let a be a given positive odd integer.
On dividing aby 4, let qbe the quotient andr be theremainder.
Then, by Eudid's algorithm, we have
a = 4m + r, where 0 < r < 4
⇒ a = 4m + r, where r = 0,1,2,3
⇒ a = 4m or a = 4m + 1 or a = 4m + 2 or a = 4m + 3
But, a = 4m and a = 4m + 2 = 2(2m + 1) are clearly even.
Thus, when ais odd, it is of the form a = (4m + 1)or (4m + 3) for some integer m.
|
126 videos|457 docs|75 tests
|
FAQs on RS Aggarwal Solutions: Real Numbers - 1 - Mathematics (Maths) Class 10
| 1. What are real numbers? |  |
| 2. How are real numbers different from rational numbers? |  |
| 3. What are the properties of real numbers? |  |
| 4. Can real numbers be negative? |  |
| 5. What is the significance of real numbers in mathematics? |  |

|
Explore Courses for Class 10 exam
|

|

















