Comparing Quantities Class 7 Notes Maths Chapter 7
| Table of contents |

|
| Introduction |

|
| Percentages |

|
| Use of Percentages |

|
| Prices Related to an Item or Buying and Selling |

|
| Charge Given on Borrowed Money or Simple Interest |

|
Introduction
Imagine you and friend Sid got your report cards, and you scored 320 out of 400 whereas Sid scored 300 out of 360. You immediately say that, you have scored better than Sid, because 320 > 300. But, is that right? Report cards also show percentages, which reveal that your percentage is 80% and Rita's is 83.3%. Mansi pointed out that comparing total marks isn't fair because the maximum possible marks are different. This means Rita actually performed better.

Percentages
Percentages are numbers that represent a part of a whole, specifically out of 100, and are used for making comparisons. Let’s look at this in more detail.
Meaning of Percentage
The term 'per cent' comes from the Latin phrase ‘per centum,’ translating to ‘for each hundred.’ The symbol for per cent is %, which indicates hundredths. So, 1% is equivalent to 1 out of 100, or one hundredth.
Percentage is a method used to compare quantities. Percent is represented by the symbol - %.
Example: What percent of ₹ 4500 is ₹ 9000?
Sol: Let us assume the percentage be Q,
Then, Q% of ₹ 4500 is ₹ 9000
⇒ (Q/100) × 4500 = ₹ 9000
⇒ (4500Q/100) = ₹ 9000
⇒ 45Q = ₹ 9000
Therefore, Q = ₹ 9000/45 = ₹ 200
Example: 30% of ₹ 360 = ________.
Sol: 30% of ₹ 360 = ₹ 108.
⇒ It can be written as = (30/100) × 360
= 10800/100
= ₹ 108
Example: 120 % of 50 km = ________.
Sol: 120 % of 50 km = 60 km.
It can be written as = (120/100) × 50
= 6000/100
= 60 km
Example: In a class of 50 students, 8 % were absent on one day. Find the number of students present on that day.
Sol: In a class of 50 students, 8 % were absent on one day. The number of students present on that day was 46.
From the question it is given that, number of students in the class = 50
Percentage of students who were absent on one day = 8%
Then, percentage of students who were present on one day = 100% – 8%
= 92%
So, 92% of 50
= (92/100) × 50
= 4600/100
= 46 students
Percentages when Total is not Hundred
Example: Consider that you have a necklace with 8 red beads and 12 blue beads. What is the percentage of red beads?
Sol: Method 1
Start by converting the fraction to an equivalent fraction with denominator 100. Like this:
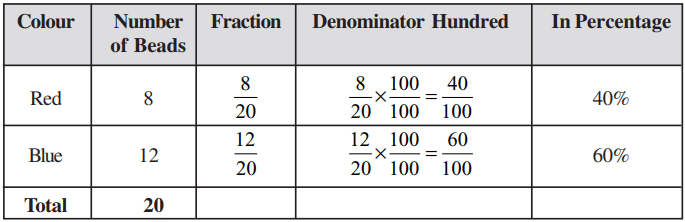
⇒ Anwar found the percentage of red beads like this:
Out of 20 beads, the number of red beads is 8.
Hence, out of 100, the number of red beads is
Hence, out of 100, the number of red beads is:
× 100 = 40%.
⇒ Asha does it like this:
= = = × 100 = 40%.
Method 2: Short-cut method
Out of 20 beads, the number of red beads is 8.
Hence, out of 100, the number of red beads is
820 × 100 = 40%.
Converting Fractional Numbers into Percentage
To compare fractional numbers, we need a common denominator. To convert a fraction into a percentage, multiply it by a hundred and then place the % symbol.
Percentages related to proper fractions are less than 100, whereas percentages related to improper fractions are more than 100.
Example: Out of 25 children in a class, 15 are girls. What is the percentage of girls?
Sol: Out of 25 children, there are 15 girls.
Therefore, the percentage of girls = × 100 = 60%
There are 60% girls in the class.
Example: Convert 5/4 to percent.
Sol: We have, x 100 = 125 %
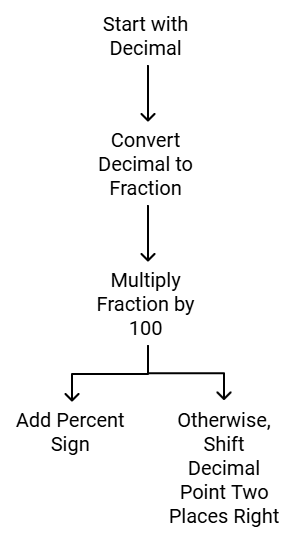
Converting Decimals to Percentages
To convert a decimal into a percentage:Step 1: Convert the decimal into a fraction.
Step 2: Multiply the fraction by 100.
Step 3: Put a percent sign next to the number. Otherwise, shift the decimal point two places to the right.
Example: 2.5 = ________%
Sol:2.5 = 2.5 x 100 %
= 25/10 × 100
= 250%
Example: Convert the given decimals to per cents:
Sol: (a) 0.75
0.75 = 0.75 × 100 % = 75/100 × 100 % = 75%
(b) 49/50
49/50 = 49/50 x 100 = 98%
(c) 0.05
0.05 = 0.05 x 100 %= 5/100 x 100 = 5%
Note: When it comes to percentages, parts always add to give a whole. This means that all the parts that form the whole, if added together, would give the whole, i.e., 100%. For example, you are given 60% of the a given number of balls are red in color. How many blue balls are there? It would be (100-60)% = 40%.
Fun with Estimation
With percentages, we can estimate the parts of an area.
Example: What part of the figure is colored?

Sol: We start by finding the fraction of the figure that is shaded. From this fraction, the percentage of the shaded part can be found.
Here, we can see that 3 out of 5 parts are shaded.
Converting into percentage: 3/5 x 100 = 60%
Therefore, 60% of the figure is shaded.
Use of Percentages
Let's have some more fun with percentages.
Converting of Percentages to "How Many"
Let's learn with an example:
Example: A survey of 40 children showed that 25% liked playing football. How many children liked playing football?
Sol: Solve such a question using the following steps:
Step 1: Write down the percentage as 'parts of the whole.'
Step 2: Find out the number
This can be solved as:
25% can be written as 25/100.
25% of 40 students can be written as 25/100 x 40
On solving, you get
25/100 x 40 = 10
Therefore, 10 children out of 40 like playing football.
Ratios to Percents
Ratios help us to compare quantities and determine the relation between them. We write ratios in the form of fractions and then compare them by converting them into like fractions. If these like fractions are equal, then we say that the given ratios are equivalent.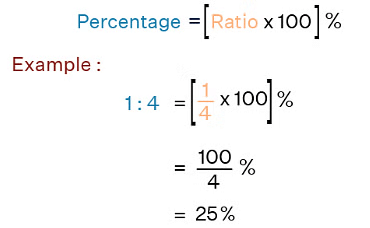 Example: The ratio of Fatima’s income to her savings is 4: 1. The percentage of money saved by her is :
Example: The ratio of Fatima’s income to her savings is 4: 1. The percentage of money saved by her is :
(a) 20% (b) 25% (c) 40% (d) 80%
Sol: (a) 20%
Let’s assume the ratio of Fatima’s income to her savings be 4x: 1x.
Then, the percentage of money saved by her is = (her savings/(income + savings)) × 100
= ( 1x / (4 x + x) ) × 100 = 1/5 x 100 = 20 %
Example: Reena’s mother said, to make idlis, you must take two parts rice and one part urad dal. What percentage of such a mixture would be rice and what percentage would be urad dal?
Sol: In terms of ratio we would write this as Rice: Urad dal = 2: 1.
Now, 2 + 1=3 is the total of all parts. This means 2/3 part is rice and 1/3 part is urad dal.
Then, percentage of rice would be (2/3) x 100 = (200/3) = 66.67%
Then, percentage of urad dal would be (1/3) x 100 = (100/3) = 33.33%
Increase or Decrease as Per Cent
Sometimes, we want to show how much something has gone up or down as a percentage. For example, if a park’s number of visitors grew from 100 to 120, it’s clearer to say the number of visitors went up by 20%.
To find out the percentage change, whether it’s an increase or decrease, look at this example:
Example: My uncle says that when he first bought a sandwich, it cost $2. Now, the same sandwich costs $6. By what percentage has the price gone up?
Sol: Let's find the solution step by step:
Find the increase in price: $6 - $2 = $4
Find the percentage increase: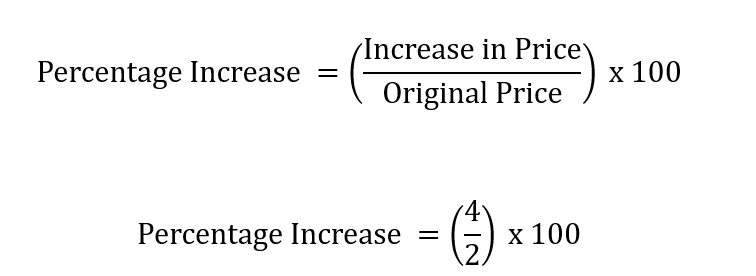 2 x 100 = 200%
2 x 100 = 200%
So, the price of the sandwich has gone up by 200%.
Prices Related to an Item or Buying and Selling
- Cost Price (CP): The buying price of an item is known as its cost price written in short as CP.
- Selling Price (SP): The price at which we sell an item is known as the selling price or in short SP. Naturally, it is better if we sell the item at a higher price than our buying price.
- Profit or Loss: We can decide whether the sale was profitable or not depending on the CP and SP.
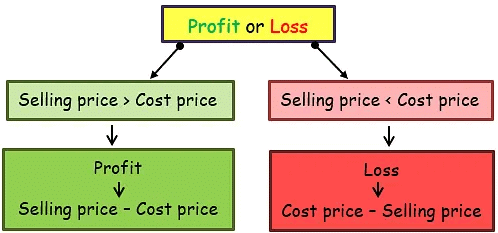 Based on the values of CP and SP, we calculate our profit or loss.
Based on the values of CP and SP, we calculate our profit or loss.
- If CP < SP then we have gained some amount, that is, we made a profit,
Profit = SP – CP - If CP = SP then we are in a no profit no loss situation
- If CP > SP then we have lost some amount,
Loss = CP – SP
Profit or Loss as a Percentage
The profit or loss we find can be converted to a percentage. It is always calculated on the CP.
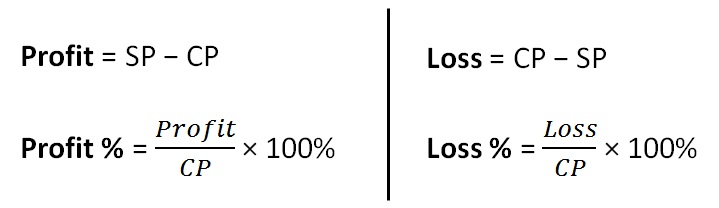
Note: If we are given any two of the three quantities related to price, that is, CP, SP, and Profit or Loss percent, we can find the third.
Example: Mohini bought a cow for ₹ 9000 and sold it at a loss of ₹ 900. The selling price of the cow is ________.
Sol: Mohini bought a cow for ₹ 9000 and sold it at a loss of ₹ 900. The selling price of the cow is ₹ 8100
From the question it is given that,
The cost price of the cow (CP) = ₹ 9000
Loss = ₹ 900
We know that, Selling price (SP) = CP – loss
= 9000 – 900 = ₹ 8100
Example: Suhana sells a sofa set for Rs. making a profit of . What is the CP of the sofa?
Sol: Let the CP of the sofa be Rs. x
Profit = 20% of x = × x =
Therefore,
SP = x + =
SP = = 9600
x = 8000
CP of the sofa set is Rs.8000.
Example: If the price of sugar is decreased by 20%, then the new price of 3kg sugar, originally costing ₹ 120 will be _____.
Sol: If the price of sugar is decreased by 20%, then the new price of 3kg sugar originally costing ₹ 120 will be ₹ 96
From the question it is given that, price of 3kg sugar originally costing ₹ 120
The price of the sugar is decreased by 20%
Then, the new price of sugar = 120 – 20% of the original price
= 120 – (20/100) × 120 = 120 – (2400/100)
= 120 – 24 = ₹ 96
Example: Aahuti purchased a house for ₹ 50,59,700 and spent ₹ 40,300 on its repairs. At what price should she sell the house to make a profit of 5%?
Sol: Aahuti purchased a house for ₹ 50,59,700 and spent ₹ 40300 on its repairs. To make a profit of 5%, she should sell the house for ₹ 5355000.
From the question it is given that,
CP of house purchased by Aahuti = ₹ 50,59,700
Amount spent to repair the house = ₹ 40,300
Total CP of house = ₹ 50,59,700 + 40,300 = ₹ 5100000
Profit % = (profit/CP) × 100 & profit = SP - CP
5 = ((SP – CP)/CP) × 100
5 = ((SP – 5100000)/5100000) × 100
(5 × 5100000)/100 = SP – 5100000 => SP = ₹ 53,55,000
Charge Given on Borrowed Money or Simple Interest
Simple Interest is a method of calculating the amount of interest charged on a sum at a given rate and for a given period of time.
- Principal: The money borrowed is known as sum borrowed or principal.
- Interest: We have to pay some extra money (or charge) to the bank for the money being used by us for some time. This is known as interest.
- Amount: We can find the amount we have to pay at the end of the year by adding the above two. That is.
Amount = Principal + Interest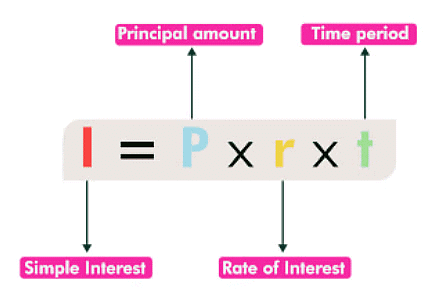 Simple Interest Calculation
Simple Interest Calculation
Example: Ramesh borrows $3,000 at an interest rate of 10% per year. How much interest will he have to pay at the end of one year?
Sol:
- Principal Amount (P): $3,000
- Rate of Interest (R): 10% per year
- Interest can be calculated as:
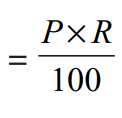
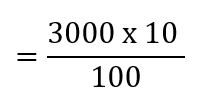
=300
So, Ramesh will have to pay $300 as interest at the end of one year.
Interest for Multiple Years
Example: Interest is typically expressed as a percentage for one year, denoted as per annum (p.a.). For instance, 10% p.a. implies that on every ₹100 borrowed, the borrower must pay ₹10 as interest for one year. This arrangement illustrates how the total amount owed is determined.
The general formula for simple interest over multiple years is derived by recognizing that the interest paid for one year on a principal amount (P) at an annual interest rate (R%) is given by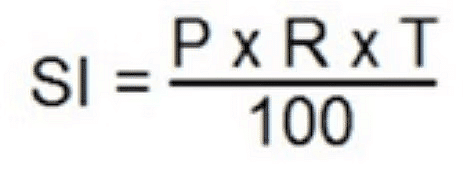
Therefore, the interest (I) paid for T years is expressed as . The total amount to be repaid at the end of T years is given by 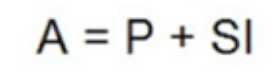 If you are provided with any two of the quantities (I, P, T, R), you can use these formulas to calculate the remaining quantity.
If you are provided with any two of the quantities (I, P, T, R), you can use these formulas to calculate the remaining quantity.
Example: Find simple interest on ₹ 12500 at 18% per annum for a period of 2 years and 4 months.
Sol: Interest on ₹ 12500 at 18% per annum for a period of 2 years and 4 months is ₹ 5250.
From the question it is given that, Principal= ₹ 12500
Time = 2 years 4 months = (2 + (4/12)) = (2 + (1/3)) = 7/3 year
Rate = 18%
Then, we know the formula of Simple interest SI = (P × R × T)/100
SI= (12500 × 18 × (7/3)) /100
SI = ₹ 5250
Example: The difference of interest for 2 years and 3 years on a sum of ₹ 2100 at 8% per annum is _________.
Sol: The difference of interest for 2 years and 3 years on a sum of ₹ 2100 at 8% per annum is ₹ 168.
From the question it is given that,
P = ₹ 2100 ,Time = 2 years, Rate = 8%
Then, we know the formula of Simple interest SI = (P × R × T)/100
SI = (2100 × 2 × 8)/100 = 33600/100 = ₹ 336
Then, taking Time = 3 years, simple interest is
SI= (2100 × 3× 8)/100 = 50400/100 = ₹504
The difference of interest for 2 years and 3 years = 3 years – 2 years
= ₹ 504 – ₹ 336
= ₹ 168
⇒
|
76 videos|452 docs|39 tests
|
FAQs on Comparing Quantities Class 7 Notes Maths Chapter 7
| 1. What is a percentage and how is it calculated? |  |
| 2. How can percentages be used in everyday life? |  |
| 3. What is the formula for calculating simple interest? |  |
| 4. How do you compare quantities using percentages? |  |
| 5. What is the significance of understanding prices related to buying and selling? |  |
















