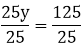Simple Equations Class 7 Notes Maths Chapter 4
| Table of contents |

|
| A Mind-Reading Game! |

|
| Setting Up an Equation |

|
| What Equation is? |

|
| Solving an Equation |

|
| More Equations |

|
| Applications of Simple Equations to Practical Situations |

|
| Word Problems |

|
A Mind-Reading Game!
Let's begin with the introduction of a new topic in mathematics, "Simple Equations." Three students, Appu, Sarita, and Ameena, are excited to present a mind-reading game to their class. The game is based on simple arithmetic operations that lead to forming equations.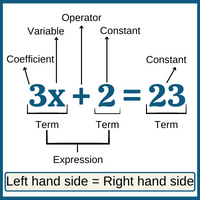
Ameena's Game:
- Ameena asks Sara to think of a number, multiply it by 4, and add 5 to the product. Sara’s final answer is 65.
- Ameena quickly guesses that the number Sara thought of was 15.
Appu's Game:
- Appu asks Balu to think of a number, multiply it by 10, and subtract 20 from the product. Balu’s result is 50.
- Appu accurately guesses that Balu's number was 7.
These examples introduce the concept of equations, where specific operations on a number result in a known outcome, and the goal is to determine the original number.
Let us explore how to solve such questions in this document.
Setting Up an Equation
To understand how Ameena and Appu were able to guess the numbers, let's break down the process: Ameena’s Example:
Ameena’s Example:- Let the unknown number Sara thought of be denoted as x.
- Sara multiplies x by 4, giving 4x, and then adds 5 to get 4x+5.
- Sara reveals that her result is 65, leading to the equation:
- Solving this equation gives the original number
Appu’s Example:
- Let the unknown number Balu thought of be denoted as y.
- Balu multiplies y by 10, giving 10y, and then subtracts 20 to get 10y−20.
- Balu reveals that his result is 50, leading to the equation: 10y−20=50
- Solving this equation gives the original number y = 7.
What Equation is?
An equation is like a balance scale. It has an equal sign in the middle, which shows that the value on the left side is the same as the value on the right side. The left side is called the LHS, and the right side is called the RHS.Example:(i) 4x + 5 = 65(ii) 10y - 20 = 50
Equality Sign: Every equation has an equality sign =, which indicates that the expressions on both sides of the equation have equal value.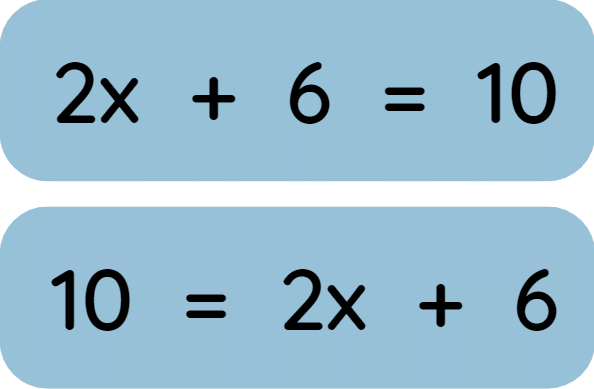 Both the above equations are the same.
Both the above equations are the same.
- In equation (i), the LHS is (4x + 5), which means we have 4 times a number (x), and we add 5 to it. The RHS is 65, which means the value on the right side is 65. So, in this equation, the value of (4x + 5) is equal to 65.
- In equation (ii), the LHS is (10y - 20), which means we have 10 times a number (y), and we subtract 20 from it. The RHS is 50, which means the value on the right side is 50. So, in this equation, the value of (10y - 20) is equal to 50.
Interchangeability:
- An equation remains the same even if the LHS and RHS are interchanged.
- Example: is the same as
Not Equations:
- If there is a sign other than the equality sign between the LHS and RHS, it is not an equation.
- Example: and are not equations because they do not express equality.
Variable on Both Sides:
- Sometimes, both sides of the equation can have expressions involving the variable.
- Example: The equation has variables on both sides.
How to form Equations using Statements?
Forming equations from statements involves translating the words into mathematical expressions. Here’s how you can do it:
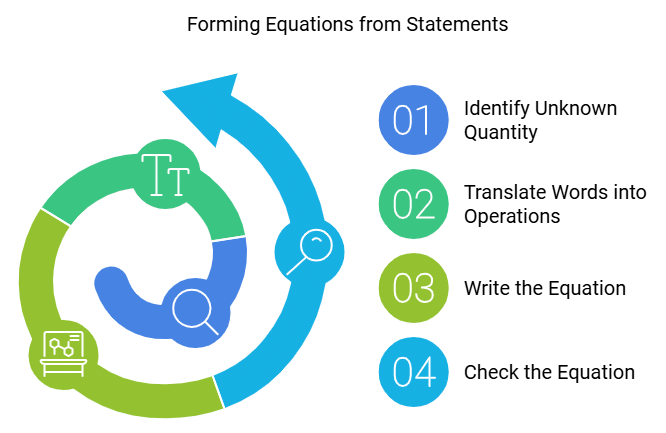 Steps to Form Equations from Statements:
Steps to Form Equations from Statements:
- Identify the Unknown Quantity: Read the statement carefully to identify the unknown quantity. Represent it using a variable (like
x,y, etc.).
Example: "A number increased by 5 is 12."
Here, the unknown number can be represented asx - Translate Words into Mathematical Operations: Convert the words into mathematical operations like addition, subtraction, multiplication, or division.
Example:- "Increased by" translates to
+. - "Is" translates to
=.
So, "A number increased by 5 is 12" becomes:x + 5 = 12.
- "Increased by" translates to
- Write the Equation: Combine the variable and the operations into a single equation.
The statement "A number decreased by 3 is equal to 7" becomes:x - 3 = 7. - Check the Equation: Make sure that the equation correctly represents the statement. Reread the statement and see if your equation makes sense.
Here are some example statements:
Example 1: The sum of four times x and 12 is equal to 35.
4x+12=35
Example 2: Half of a number is 3 more than 8.
1/2x - 8 = 3
Example 3: Write the following statements in the form of equations:
(i) The sum of four times x and 12 is 38.
(ii) If you subtract 4 from 6 times a number, you get 8
(iii) One third of m is 6 more than 9.
(iv) One fourth of a number plus 7 is 10.
Solution:
(i) Four times x is 4x.
Sum of 4x and 12 is 4x + 12. The sum is 38.
The equation is 4x + 12 = 38.
(ii) Let us say the number is z; z multiplied by 6 is 6z.
Subtracting 4 from 6z, one gets 6z – 4. The result is 8.
The equation is 6z – 4 = 8
(iii) One third of m is m / 3. It is greater than 9 by 6.
This means the difference ( m / 3 – 9) is 6.
The equation is (m / 3) – 9 = 6
(iv) Take the number to be n. One fourth of n is n / 4. This one-fourth plus 7 is (n/4) + 7. It is 10. The equation is (n / 4) + 7 = 10
Example 4: A store sells apples in two types of bags, one small and one large. A large bag contains as many as 6 small bags plus 3 loose apples. Set up an equation to find the number of apples in each small bag. The number of apples in a large bag is given to be 75.
Solution:
Let a small bag contain 'a' number of apples.
A large bag contains 3 more than 6 times 'a', that is, 6a + 3 apples.
But this is given to be 75. Thus, 6a + 3 = 75.
You can determine the number of apples in a small bag by solving this equation.
Example 5: Write the following statements in the form of equations:
(i) The sum of three times x and 11 is 32.
(ii) If you subtract 5 from 6 times a number, you get 7.
Solution:
(i) Three times x is 3x.
Sum of 3x and 11 is 3x + 11.
The sum is 32.
The equation is 3x + 11 = 32.
(ii) Let us say the number is z;
z multiplied by 6 is 6z.
Subtracting 5 from 6z, one gets 6z – 5.
The result is 7.
The equation is 6z – 5 = 7
The sum of three times x and 10 is 13.
How to Convert Equation into Statement?
Converting an equation into a statement involves expressing the mathematical equation in words. Here's how you can do it:
- Step 1: Identify the variables in the equation. Variables are represented by letters, such as x, y, a, b, etc.
- Step 2: Determine the operations being performed on the variables. Common operations include addition (+), subtraction (-), multiplication (*), and division (/).
- Step 3: Translate the equation into words, describing the operations in simple terms.
- Step 4: Write the statement in a clear and understandable manner.
Here are some example questions:
Example 6: Convert the equation into a statement by yourself:
(i) x + 3 = 7
(ii) 4y = 16
(iii) 2a - 5 = 9
(iv) 7b + 3 = 24
Solution:
(i) x + 3 = 7 -Adding 3 to x gives 7.
(ii) 4y = 16 - Four times a number y is equal to 16.
(iii) 2a - 5 = 9 - Subtracting 5 from twice a number a gives 9.
(iv) 7b + 3 = 24 - Adding 3 to seven times a number b results in 24.
Example 7: Write the following statements in the form of equations:
(i) The sum of three times x and 11 is 32.
(ii) If you subtract 5 from 6 times a number, you get 7.
Solution:
(i) Three times x is 3x.
Sum of 3x and 11 is 3x + 11.
The sum is 32.
The equation is 3x + 11 = 32.
(ii) Let us say the number is z;
z multiplied by 6 is 6z.
Subtracting 5 from 6z, one gets 6z – 5.
The result is 7.
The equation is 6z – 5 = 7
Example 8: Convert the following equations in statement form:
(i) x – 5 = 9
(ii) 5p = 20
(iii) 3n + 7 = 1
Solution:
(i) Taking away 5 from x gives 9.
(ii) Five times a number p is 20.
(iii) Add 7 to three times n to get 1.
Example 9: Check whether the value given in the brackets is a solution to the given equation or not:
(a) n + 5 = 19 (n = 1)
(b) 7n + 5 = 19 (n = – 2)
Solution: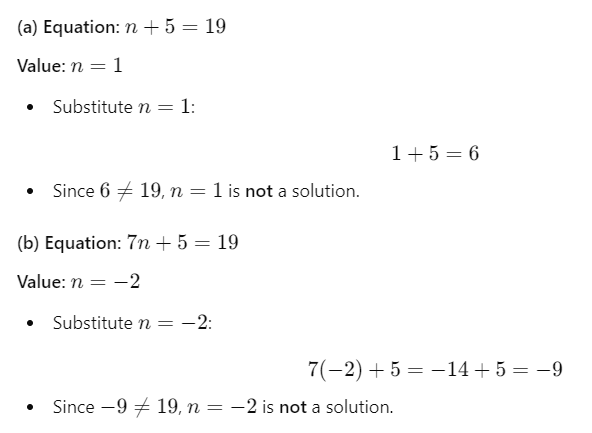
Solving an Equation
Any value of the variable that satisfies the equation is the solution of the equation.
1. Understanding Equality:
Consider the equation: Both sides are equal, making the equality valid.
2. By adding or subtracting the same number to both sides of the equation.
Example: x + 11 = 35
Solution:
Subtract 11 from both sides.
x + 11 – 11 = 35 – 11x = 24
Here, x = 24 is the solution of the given equation.
3. By multiplying or dividing by the same non-zero number to both sides of the equation.
Example : 25y = 125
Solution:
Divide both sides by 25.
y = 5
4. What Happens if Operations Differ on Both Sides?
If different operations or numbers are applied to each side, the equality does not hold.
Example:
- Add 2 to LHS and 3 to RHS:
New LHS=8−3+2=7, New RHS=4+1+3=8- The equality is lost since
5. Weighing Balance Analogy: An equation is like a balance scale. If the same weights (numbers) are added or removed from both sides, the scale remains balanced (equality holds).
6. Choosing the Correct Operation:
The correct operation to isolate the variable depends on the equation. Sometimes multiple operations are required to solve the equation.
Here are some example questions:
Example 10: Give first the step you will use to separate the variable and then solve the equation:
(a) x – 1 = 0
(b) x + 1 = 0
Solution:
Example 11: Give first the step you will use to separate the variable and then solve the equation:
Solution: 
Example 12: Give the steps you will use to separate the variable and then solve the equation:
(a) 3n – 2 = 46
(b) 5m + 7 = 17 
More Equations
Let's learn about Transposing Method
In this method, we transpose the numbers from one side of the equation to the other side so that all the terms with variables come on one side and all the constants come on another side.
While transposing the numbers, the sign of the terms will get changed. i.e. Negative will become positive and positive will become negative.
Example 13: x + 11 = 35
Solution:
Now we will transfer 11 from LHS to RHS and its sign will get reversed.
x = 35 – 11
x = 24
Example 14: Solve 20y + y - 18 = 10y + 2y
Sol: 21y - 18 = 12y
21y - 12y = 18
9y = 18 (By dividing both sides by 9)
y = 2
The digit at the unit's place is y = 2.
And the digit at the tens place is 2y = 2 × 2 = 4
Hence, the required number is 42.
 Add/Subtract on both sides Vs Transposing
Add/Subtract on both sides Vs Transposing
Applications of Simple Equations to Practical Situations
From a Solution to the Equation
As we solve the equation to get the solution, we can get the equation also if we have the solution. Any equation has only one solution but if we make an equation from a solution then there could be many equations.

Example 15: Sara is twice as old as her brother John. Five years ago, Sara was three times as old as John. How old is Sara now?
Solution:
Let John's current age be x years.
Since Sara is twice as old as John, Sara's current age is 2x years.
According to the problem, five years ago, Sara was three times as old as John. So, we can write the equation:
2x3(x
To find their ages, solve for x:
First, simplify the right side of the equation:
2x−5=3x−15
Next, isolate x by subtracting 3x from both sides:
2x−3x−5=−15
−x−5 = −15
Add 5 to both sides to isolate −x:
−x = −10
Multiply both sides by -1:
x=10
So, John is 10 years old.
Since Sara is twice as old as John:
2x=2×10=20
Therefore, Sara is 20 years old.
This is not the only possible equation. There could be other equations also.
Word Problems
Example 16: Radha’s Mother’s age is 5 years more than three times Shikha’s age. Find Shikha’s age, if her mother is 44 years old.
Solution:
Let Shikha’s age = y years
Her mother’s age is 3y + 5 which is 44.
Hence, the equation for Shikha’s age is 3y + 5 =44
3y + 5 = 44
3y = 44 – 5 (by transposing 5)
3y = 39
y = 13 (by dividing both sides by 3)
Hence, Shikha’s age = 13 years
Example 17: A number consists of two digits. The digit in the tens place is twice the digit in the units place. If 18 is subtracted from the number, the digits are reversed. Find the number.
Solution:
Let the digit at units place = y
So, the digit in the tens place = 2y
So, the number is (2y) y.
As it is given that if 18 is subtracted from the number, the digits are reversed.
So, we have
(2y) y - 18 = y(2y)
10 × (2y) + 1 × y - 18 = 10 × y + 1 × (2y)
We hope you've understood the chapter well. Here's a video to help you understand it even better:
|
76 videos|452 docs|39 tests
|
FAQs on Simple Equations Class 7 Notes Maths Chapter 4
| 1. What is an equation in mathematics? |  |
| 2. How can an equation be converted into a statement? |  |
| 3. How do you solve an equation in mathematics? |  |
| 4. Can you provide examples of more equations? |  |
| 5. How are simple equations applied to practical situations? |  |