NCERT Exemplar Solutions: Fractions & Decimals | Mathematics (Maths) Class 7 (Old NCERT) PDF Download
Exercise Page: 38
In questions 1 to 20, out of four options, only one is correct. Write the correct answer.
Q.1. (2/5) × 5(1/5) is equal to:
(a) 26/25
(b) 52/25
(c) 2/5
(d) 6
Ans: b
Solution: First we have to convert the mixed fraction into improper fraction
5(1/5)
= 26/5
Then, (2/5) × (26/5)
= 52/25
Q.2. 3¾ ÷ ¾ is equal to:
(a) 3
(b) 4
(c) 5
(d) 45/16
Ans: c
Solution: First we have to convert the mixed fraction into improper fraction 3¾ = 15/4
Then, 15/4 ÷ ¾
= (15/4)/ (¾)
= (15/4) × (4/3)
= (15 × 4)/ (4 ×3)
= (5 × 1)/ (1 ×1)
= 5
Q.3. A ribbon of length 5¼ m is cut into small pieces each of length ¾m. Number of pieces will be:
(a) 5
(b) 6
(c) 7
(d) 8
Ans: c
Solution: First we have to convert the mixed fraction into improper fraction 5¼ = 21/4
Then, 21/4 ÷ ¾
= (21/4)/ (¾)
= (21/4) × (4/3)
= (21 × 4)/ (4 × 3)
= (7 × 1)/ (1 × 1)
= 7
Q.4. The ascending arrangement of (2/3), (6/7), (13/21) is:
(a) 6/7, 2/3, 13/21
(b) 13/21, 2/3, 6/7
(c) 6/7, 13/21, 2/3
(d) 2/3, 6/7, 13/21
Ans: b
Solution: LCM of 21, 3, 7 = 21
Now, let us change each of the given fraction into an equivalent fraction having 21 as the denominator.
[(13/21) × (1/1)] = (13/21)
[(2/3) × (7/7)] = (14/21)
[(6/7) × (3/3)] = (18/21)
Clearly,
(13/21) < (14/21) < (18/21)
Hence,
(13/21) < (2/3) < (6/7)
Hence, the given fractions in ascending order are (13/21), (2/3), (6/7)
Q.5. Reciprocal of the fraction 2/3 is:
(a) 2
(b) 3
(c) 2/3
(d) 3/2
Ans: d
Solution: The reciprocal of a non-zero fraction is obtained by interchanging its numerator and denominator.
Q.6. The product of 11/13 and 4 is:
(a) 3(5/13)
(b) 5(3/13)
(c) 13(3/13)
(d) 13(5/13)
Ans: a
Solution:
11/13 x 4 = 11/13 x 4/1 = 44/13 = 3(5/13)
Q.7. The product of 3 and 4(2/5) is:
(a) 17(2/5)
(b) 24/5
(c) 13(1/5)
(d) 13(5/3)
Ans: d
Solution: First we have to convert the mixed fraction into improper fraction 4(2/5) = 22/5
then 3 x 22/5
= 66/5
=13(1/5)
Q.8. Pictorial representation of 3 × 2/3 is:
(a) 
(b) 
(c) 
(d) 
Ans: b
Solution:
In the above figure, three circles are divided into 3 equal parts.
Out of 3 equal parts 2 equal parts are hatched.
Q.9. 1/5 ÷ 4/5 equal to:
(a) 4/5
(b) 1/5
(c) 5/4
(d) ¼
Ans: d
Solution:
= 1/5 ÷ 4/5
= (1/5)/ (4/5)
= (1/5) × (5/4)
= 5/20 … [divide both numerator and denimonitor by 5]
= ¼
Q.10. The product of 0.03 × 0.9 is:
(a) 2.7
(b) 0.27
(c) 0.027
(d) 0.0027
Ans: c
Solution:
0.03 × 0.9 can be written as = (3/100) × (9/10)
= 27/1000
On dividing a decimal by 1000, the decimal point is shifted to the left by three places.
= 0.027
Q.11. (5/7) ÷ 6 is equal to:
(a) 30/7
(b) 5/42
(c) 30/42
(d) 6/7
Ans: b
Solution:
= 5/7 ÷ 6/1
= (5/7)/ (6/1)
= (5/7) × (1/6)
= 5/42
Q.12. 5(1/6) ÷ 9/2 is equal to:
(a) 31/6
(b) 1/27
(c) 5(1/27)
(d) 31/27
Ans: d
Solution: First we have to convert the mixed fraction into improper fraction
5(1/6) = 31/6
Then,
= 31/6 ÷ 9/2
= (31/6)/ (9/2)
= (31/6) × (2/9)
= (31/3) × (1/9)
= 31/27
Q.13. Which of the following represents 1/3 of 1/6 ?
(a) (1/3) + (1/6)
(b) (1/3) – (1/6)
(c) (1/3) × (1/6)
(d) (1/3) ÷ (1/6)
Ans: c
Solution:
1/3 of 1/6 = 1/3 x 1/6
Q.14. 3/7 of 2/5 is equal to
(a) 5/12
(b) 5/35
(c) 1/35
(d) 6/35
Ans: d
Solution:
3/7 of 2/5 is equal to = (3/7) × (2/5)
= 6/35
Q.15. One packet of biscuits requires 2½ cups of flour and 1(2/3) cups of sugar. Estimated total quantity of both ingredients used in 10 such packets of biscuits will be
(a) less than 30 cups
(b) between 30 cups and 40 cups
(c) between 40 cups and 50 cups
(d) above 50 cups
Ans: c
Solution: From the question it is given that,
One packet of biscuits requires 2½ cups of flour = 5/2
One packet of biscuits requires 1(2/3) cups of sugar. = 5/3
Total ingredients for one packet of biscuits = (5/2) + (5/3)
= (15 + 10)/6
= 25/6
Then, total quantity of both ingredients used in 10 such packets of biscuits = 10 × (25/6)
= 5 × (25/3)
= 125/3
= 41(2/3)
Q.16. The product of 7 and 6¾ is
(a) 42¼
(b) 47¼
(c) 42¾
(d) 47¾
Ans: b
Solution: First we have to convert the mixed fraction into improper fraction 6¾ = 27/4
= 7 × (27/4)
= 189/4
= 47¼
Q.17. On dividing 7 by 2/5, the result is
(a) 14/2
(b) 35/4
(c) 14/5
(d) 35/2
Ans: d
Solution:
= 7/ (2/5)
= 7 × (5/2)
= 35/2
Q.18. 2(2/3) ÷ 5 is equal to
(a) 8/15
(b) 40/3
(c) 40/5
(d) 8/3
Ans: a
Solution: First we have to convert the mixed fraction into improper fraction
2(2/3) = 8/3
Then,
= (8/3) ÷ 5
= (8/3)/(5/1)
= (8/3) × (1/5)
= 8/15
Q.19. 4/5 of 5 kg apples were used on Monday. The next day 1/3 of what was left was used. Weight (in kg) of apples left now is
(a) 2/7
(b) 1/14
(c) 2/3
(d) 4/21
Ans: c
Solution: From the question it is given that,
4/5 of 5 kg apples were used on Monday = (4/5) × 5
= 20/5
= 4 kg
Then,
The next day 1/3 of what was left was used = (1/3) × 1
= 1/3 kg
So, Weight (in kg) of apples left now is = 1 – (1/3)
= (3 – 1)/3
= 2/3 kg of apples
Q.20. The picture 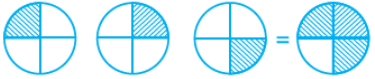
Interprets
(a) ¼ ÷ 3
(b) 3 × ¼
(c) ¾ × 3
(d) 3 ÷ ¼
Ans: b
Solution: From the given picture, ¼ + ¼ + ¼ = ¾
In Questions 21 to 44, fill in the blanks to make the statements true.
Q.21. Rani ate 2/7 part of a cake while her brother Ravi ate 4/5 of the remaining. Part of the cake left is
Ans: Rani ate 2/7 part of a cake while her brother Ravi ate 4/5 of the remaining. Part of the cake left is 1/7.
Now, let us assume total part of cake be 1.
Then, from the question, given that Rani ate 2/7 part of a cake = 1 – (2/7)
= (7 – 2)/7
= 5/7
So, Ravi ate 4/5 of the remaining cake = (4/5) × (5/7)
= 4/7
Therefore, the part of the cake left = (5/7) – (4/7)
= 1/7
Q.22. The reciprocal of 3/7 is
Ans: The reciprocal of 3/7 is 7/3
The reciprocal of a non-zero fraction is obtained by interchanging its numerator and denominator.
Q.23. 2/3 of 27 is
Ans: 2/3 of 27 is 18.
= 2/3 × 27
= 2 × 9
= 18
Q.24. 4/5 of 45 is
Ans: 4/5 of 45 is 36.
= 4/5 × 45
= 4 × 9
= 36
Q. 25. 4 × 6(1/3) is equal to
Ans: 4 × 6(1/3) is equal to 76/3
First we have to convert the mixed fraction into improper fraction
6(1/3) = 19/3
Then, 4 × 19/3
= 76/3
Q.26. ½ of 4(2/7) is
Ans: ½ of 4(2/7) is 15/7.
First we have to convert the mixed fraction into improper fraction
4(2/7) = 30/7
Then, ½ × (30/7)
= 15/7
Q.27. 1/9 of 6/5 is
Ans: 1/9 of 6/5 is 2/15.
= (1/9) × (6/5)
= (1/3) × (2/5)
= 2/15
Q.28. The lowest form of the product
2(3/7) × (7/9) is
Ans: The lowest form of the product
2(3/7) × (7/9) is (17/9) or
1(8/9)
First we have to convert the mixed fraction into improper fraction
2(3/7) = 17/7
Then, (17/7) × (7/9)
= 17/9
= 1(8/9)
Q.29. (4/5) ÷ 4 is equal to
Ans: (4/5) ÷ 4 is equal to 1/5.
= (4/5) ÷ 4
= (4/5) × (¼)
= (1/5) × (1/1)
= 1/5
Q.30. 2/5 of 25 is
Ans: 2/5 of 25 is 10
= 2/5 × 25
= 2 × 5
= 10
Q.31. (1/5) ÷ (5/6) = (1/5) (6/5)
Ans: (1/5) ÷ (5/6) = (1/5) × (6/5)
While dividing one fraction by another fraction, we multiply the first fraction by the reciprocal of the other.
Q.32. 3.2 × 10 = ______.
Ans: 3.2 × 10 = 32
To multiply a decimal number by 10, we move the decimal point in the number to the right by as many places as many zeros (0) are at the right of one.
Q.33. 25.4 × 1000 = ______.
Ans: 25.4 × 1000 = 25400
To multiply a decimal number by 1000, we move the decimal point in the number to the right by as many places as many zeros (0) are at the right of one.
Q.34. 93.5 × 100 = ______.
Ans: 93.5 × 100 = 9350
To multiply a decimal number by 100, we move the decimal point in the number to the right by as many places as many zeros (0) are at the right of one.
Q.35. 4.7 ÷ 10 = ______.
Ans: 4.7 ÷ 10 = 0.47
To divide a decimal number by 10, shift the decimal point in the decimal number to the left by as many places as there are zeros over 1, to get the quotient.
= 4.7/10
= 0.47
Q.36. 4.7 ÷ 100 = ______.
Ans: 4.7 ÷ 100 = 0.047
To divide a decimal number by 100, shift the decimal point in the decimal number to the left by as many places as there are zeros over 1, to get the quotient.
= 4.7/100
= 0.047
Q.37. 4.7 ÷ 1000 = ______.
Ans: 4.7 ÷ 1000 = 0.0047
To divide a decimal number by 1000, shift the decimal point in the decimal number to the left by as many places as there are zeros over 1, to get the quotient.
= 4.7/1000
= 0.0047
Q.38. The product of two proper fractions is ______ than each of the fractions that are multiplied.
Ans: The product of two proper fractions is less than each of the fractions that are multiplied.
Consider the two proper fractions, 4/5 and 2/4
= (4/5) × (2/4)
= 2/5
= 0.4
Then, 0.4 is multiplied to the proper fraction less than each of the fractions that are multiplied = (4/5) × 0.4
= 0.32
Q.39. While dividing a fraction by another fraction, we ______ the first fraction by the ______ of the other fraction.
Ans: While dividing a fraction by another fraction, we multiply the first fraction by the reciprocal of the other fraction.
Example,
= (1/5) ÷ (5/6)
= (1/5) × (6/5)
Q.40. 8.4 ÷ = 2.1
Ans: 8.4 ÷ 4 = 2.1
Let us assume the missing fraction be x,
Then,
8.4 ÷ x = 2.1
8.4/x = 2.1
By cross multiplication, we get,
x = 8.4/2.1
x = 84/21 … [divide both numerator and denominator by 3]
x = 28/7 … [divide both numerator and denominator by 7]
x = 4
Q.41. 52.7 ÷ ______ = 0.527
Ans: 52.7 ÷ 100 = 0.527
Let us assume the missing fraction be x,
Then,
52.7 ÷ x = 0.527
52.7/x = 0.527
By cross multiplication, we get,
x = 52.7/0.527
x = 52700/527 … [divide both numerator and denominator by 527]
x = 100
Q.42. 0.5 ______ 0.7 = 0.35
Ans: 0.5 × 0.7 = 0.35
While multiplying two decimal numbers, first multiply them as whole numbers. Count the number of digits to the right of the decimal point in both the decimal numbers. Add the number of digits counted. Put the decimal point in the product by counting the number of digits equal to sum obtained from its rightmost place.
= 0.5 × 0.7
= 5 × 7
= 35
= 0.35
Q.43. 2 (5/3) = 10/3
Ans: 2 × (5/3) = 10/3
Q.44. 2.001 ÷ 0.003 = ______.
Ans: 2.001 ÷ 0.003 = 667
= 2.001/0.003
= 2001/3 … [divide both numerator and denominator by 3]
= 667
In each of the Questions 45 to 54, state whether the statement is True or False.
Q.45. The reciprocal of a proper fraction is a proper fraction.
Ans: False.
Consider the proper fraction 5/8.
Then, reciprocal of 5/8 = 8/5.
Therefore the obtained fraction is improper fraction.
Q.46. The reciprocal of an improper fraction is an improper fraction.
Ans: False.
Consider the improper fraction 5/3.
Then, reciprocal of 5/3 = 3/5.
Therefore the obtained fraction is proper fraction.
Q.47. Product of two fractions = (Product of their denominators)/ (Product of their numerators)
Ans: False.
Product of two fractions = (Product of their numerators)/ (Product of their denominators)
Q.48. The product of two improper fractions is less than both the fractions.
Ans: False.
The product of two improper fractions is more than each of the fractions that are multiplied.
Consider the two improper fractions, 5/4 and 4/2
= (5/4) × (4/2)
= 5/2
= 2.5
Then, 2.5 is multiplied to the improper fraction more than each of the fractions that are multiplied = (5/4) × 2.5
= 3.125
And (4/2) × 2.5 = 5
Q.49. A reciprocal of a fraction is obtained by inverting it upside down.
Ans: True.
Reciprocal of 8/9 = 9/8
Q.50. To multiply a decimal number by 1000, we move the decimal point in the number to the right by three places.
Ans: True.
To multiply a decimal number by 1000, we move the decimal point in the number to the right by as many places as many zeros (0) are at the right of one.
2.5 × 1000 = 2500
Q.51. To divide a decimal number by 100, we move the decimal point in the number to the left by two places.
Ans: True.
Example: 3.4/100 = 0.034
Q.52. 1 is the only number which is its own reciprocal.
Ans: True.
We know that, if the denominator is not given then we have to assume 1 always.
So, reciprocal of 1/1 = 1/1
Q.53. 2/3 of 8 is same as (2/3) ÷ 8
Ans: False.
2/3 of 8 = (2/3) × 8
Q.54. The reciprocal of 4/7 is 4/7
Ans: False.
The reciprocal of 4/7 is 7/4.
Q.55. If 5 is added to both the numerator and the denominator of the fraction 5/9, will the value of the fraction be changed? If so, will the value increase or decrease?
Ans: If 5 is added to both the numerator and denominator of the fraction 5/9 = 10/14
But, 5/9 ≠ 10/14
Yes the value of the fraction is changed and also the value is increased.
Q.56. What happens to the value of a fraction if the denominator of the fraction is decreased while numerator is kept unchanged?
Ans: The value of a fraction is increased when the denominator of the fraction is decreased while numerator is kept unchanged.
Example: ¼ = 0.25
½ = 0.5
Q.57. Which letter comes 2/5 of the way among A and J?
Ans: There are 10 letters from A to J
So, 2/5 of 10 = 2/5 × 10
= 2 × 2
= 4
The 4th letter from A to J is D.
Therefore, D comes 2/5 of the way among A and J.
Q.58. If 2/3 of a number is 10, then what is 1.75 times of that number?
Ans: From the question it is given that,
2/3 of a number is 10.
Let us assume the number be ‘P’.
Then,
2/3 of P = 10
2/3 × P = 10
By cross multiplication we get,
P = 10 × 3/2
P = 5 × 3
P = 15
So, the number is 15
Again it is given in question that, 1.75 times of that number = ?
= 1.75 of 15
= 1.75 × 15
= 26.25
Q.59. In a class of 40 students, 1/5 of the total number of students like to eat rice only, 2/5 of the total number of students like to eat chapati only and the remaining students like to eat both. What fraction of the total number of students like to eat both?
Ans: From the question it is given that,
Number of students in a class = 40 students
1/5 of the total number of students like to eat rice only = 1/5 × 40
= 1 × 8
= 8 students
2/5 of the total number of students like to eat chapati only = 2/5 × 40
= 2 × 8
= 16 students
Then,
Number of students like to eat both = 40 – (8 + 16)
= 40 – 24
= 16 students
Fraction of the total number of students like to eat both = 16/40 = 2/5
Q.60. Renu completed 2/3 part of her home work in 2 hours. How much part of her home work had she completed in 1¼ hours?
Ans: From the question it is given that,
Renu completed 2/3 part of her home work in 2 hours.
Let us assume total part of homework be ‘P’.
Then,
2/3 of P = 2
2/3 × P = 2
By cross multiplication we get,
P = 2 × 3/2
P = 3 home work
So, part of her home work she had completed in 1¼ hours i.e. 5/4 hours
Let us assume part of home work she had completed in 5/4 hours be = Q
Then,
Q of 3 = 5/4
Q × 3 = 5/4
By cross multiplication we get,
Q = (5/4) × (1/3)
Q = 5/12
Therefore, Renu completed 5/12 part of her home work in 5/4 hours.
Q.61. Reemu read (1/5)th pages of a book. If she reads further 40 pages, she would have read (7/10)th pages of the book. How many pages are left to be read?
Ans: From the question it is given that,
Reemu read (1/5)th pages of a book.
Let us assume the total number of pages in the book be ‘P’.
Then, number of pages read by Reemu = (1/5) of P
= (1/5) × P
And also it is given in the question, If she reads further 40 pages, she would have read (7/10)th pages of the book. = (7/10) × P
So,
((1/5) × P) + 40 = (7/10) × P
(P + 200)/5 = (7P/10)
By cross mutliplication we get,
2P + 400 = 7P
5P = 400
P = 400/5 … [divide both numerator and denominator by 5]
P = 80
Then, pages read by Reemu = Total pages – Pages read
P – (7P/10) = (3P/10)
(3/10) × 80
24 pages
Therefore, 24 pages are left to be read.
Q.62. Write the number in the box  such that
such that
Ans: Let us assume the missing number be P.
Then,
(3/7) × P = 15/98
By cross multiplication we get,
P = (15/98) × (7/3)
P = (5/14) × (1/1)
P = 5/14
Therefore,
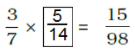
Q.63. Will the quotient 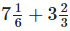 be a fraction greater than 1.5 or less than 1.5? Explain.
be a fraction greater than 1.5 or less than 1.5? Explain.
Solution: We have, 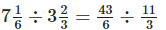
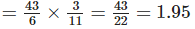
Since, 1.95 > 1.5
∴ The quotient of 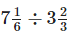 is a fraction greater than 1.5.
is a fraction greater than 1.5.
Q.64. Describe two methods to compare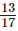 and 0.82. Which do you think is easier and why?
and 0.82. Which do you think is easier and why?
Solution:
Method I: Conversion of both numbers 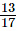 and 0.82 into decimals
and 0.82 into decimals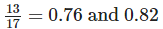
Method II: Conversion of both numbers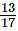 and 0.82 into fractions
and 0.82 into fractions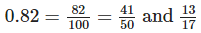
∴ Method of converting numbers into decimals is easier because we can easily compare the numbers in this method but in other method we will also convert the fractions into like fractions to compare the numbers.
Q.65. Health: The directions for a pain reliever recommend that an adult of 60 kg and over take 4 tablets every 4 hours as needed, and an adult who weighs between 40 and 50 kg take only 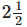 tablets every 4 hours as needed. Each tablet weighs
tablets every 4 hours as needed. Each tablet weighs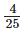 gram.
gram.
(a) If a 72 kg adult takes 4 tablets, how many grams of pain reliever is he or she receivings?
(b) How many grams of pain reliever is the recommended dose for an adult weighing 46 kg?
Solution:
(a) Each tablet weighs 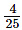 gram
gram
∴Weight of 4 tablets = 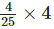 gram
gram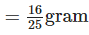
(b) An adult weighing 46 kg takes only 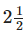 tablets.
tablets.
∴ weight of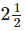 tablets =
tablets =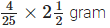

Q.66. Animals: The label on a bottle of pet vitamins lists dosage guidelines. What dosage would you give to each of these animals?
(a) a 18 kg adult dog
(b) a 6 kg cat
(c) a 18 kg pregnant dog

Solution:
(a) Total dosage given to a 18 kg adult dog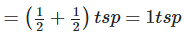
(b) Total dosage given to a 6 kg cat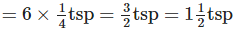
(c) Total dosage given to a 18 kg pregnant dog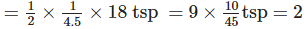
Q.67. How many 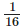 kg boxes of chocolates can be made with
kg boxes of chocolates can be made with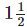 kg chocolates?
kg chocolates?
Solution: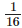 kg chocolates to be filled in 1 box.
kg chocolates to be filled in 1 box.
∴ 1 kg chocolates to be filled in 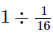
= 1 × 16 = 16 boxes.
Now, 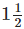 kg chocolates to be filled in
kg chocolates to be filled in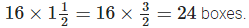
Q.68. Anvi is making bookmarker like the one shown in the given figure. How many bookmarker can she make from a 15 m long ribbon?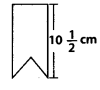
Solution:
Length of one bookmarker =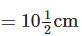
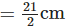
∴ Number of bookmarker Anvi can make from 15 m ix., 15 × 100 cm long ribbon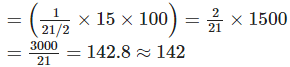
Thus, Anvi can make 142 bookmaker from a 15 m long ribbon.
Q.69. A rule for finding the approximate length of diagonal of a square is to multiply the length of a side of the square by 1.414. Find the length of the diagonal when :
(a) The length of a side of the square is 8.3 cm.
(b) The length of a side of the square is exactly 7.875 cm.
Solution:
(a) Length of a side of the square = 83 cm
∴ Length of the diagonal of the square
= 1.414 × 8.3 cm = 11.7362 cm
≈ 11.74 cm
(b) Length of a side of the square = 7.875 cm
Length of the diagonal of the square
= 1.414 × 7.875 cm
= 11.13525 cm
≈ 11.14 cm
Q.70. The largest square that can be drawn in a circle has a side whose length is 0.707 times the diameter of the circle. By this rule, find the length of the side of such a square when the diameter of the circle is
(a) 14.35 cm
(b) 8.63 cm
Solution: (a) Diameter of the circle = 14.35 cm ..
∴ Length of the side of the square
= 0.707 × 14.35 cm
= 10.14545 = 10.15 cm
(b) Diameter of the circle = 8.63 cm
∴ Length of the side of the square
= 0.707 × 8.63 cm
= 6.10141 cm = 6.10 cm
Q.71. To find the distance around a circular disc, multiply the diameter of the disc by 3.14. What is the distance around the disc when :
(a) the diameter is 18.7 cm?
(b) the radius is 6.45 cm?
Solution:
(a) Diameter of the disc = 18.7 cm
∴ The distance around the disc
= 3.14 × 18.7 cm = 58.718 cm
(b) Radius of the disc = 6.45 cm
∴ Diameter of the disc = 2 × 6.45 cm = 12.9 cm
∴ The distance around the disc
= 3.14 × 12.9 cm = 40.506 cm
Q.72. What is the cost of 27.5 m of cloth at Rs. 53.50 per metre?
Solution: Cost of 1 metre of cloth = Rs. 53.50
∴ Cost of 275 metres of cloth = Rs. (53.50 × 27.5) = Rs. 1471.25
Q.73. In a hurdle race, Nidhi is over hurdle B and 2/6 of the way through the race, as shown in the given figure.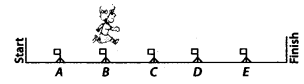
Then, answer the following:
(a) Where will Nidhi be, when she is 4/6 of the way through the race?
(b) Where will Nidhi be when she is 5/6 of the way through the race?
(c) Give two fractions to tell what part of the race Nidhi has finished when she is over hurdle C.
Solution:
(a) When Nidhi is 4/6 of the way through the race, she will be at hurdle D.
(b) When Nidhi is 5/6 of the way through the race, she will be at hurdle E.
(c) When Nidhi is over hurdle C, she would finished the 3/6 or 1/2 or middle part of the race.
Q.74. Diameter of Earth is 12756000 m. In 1996, a new planet was discovered whose diameter is 5/86 of the diameter of Earth. Find the diameter of this planet in km.
Solution: Diameter of Earth = 12756000 m
Diameter of a new planet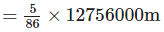
= 741627.90 m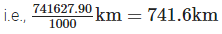
Q.75. What is the product of 5/129 reciprocal?
Solution: The reciprocal of 5/129 = 129/5
Q.76. Simplify: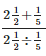
Solution: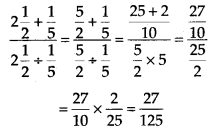
Q.77. Simplify: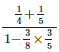
Solution: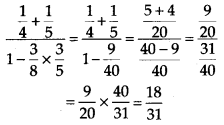
Q.78. Divide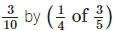
Solution: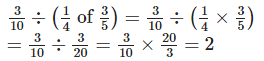
Q.79.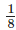 of a number equals
of a number equals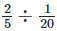 number?
number?
Solution:
Let the number be x.
According to question,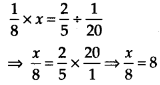
⇒ x = 64
Hence, the required number is 64.
Q.80. Heena’s father paid an electric bill of Rs. 95.70 out of a 500 rupee note. How much change should he have received?
Solution: The amount of money Heena’s father has = Rs. 500
He paid an electric bill of Rs. 95.70
∴ The amount of money he should have received = Rs. (500 – 95.70) = Rs. 404.30
Q.81. The normal body temperature is 98.6°F. When Savitri was ill her temperature rose to 103.1°F. How many degrees above normal was that?
Solution: The normal body temperature = 98.6°F
Savitri’s temperature, when she was ill = 103.1°F
∴ Savitri’s temperature above normal
= 103.1°F – 98.6°F
= 4.5°F
Q.82. Meteorology: One measure of average global temperature shows how each year varies from a base measure. The table shows results for several years.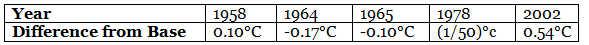
See the table and answer the following:
(a) Order the five years from coldest to warmest.
(b) In 1946, the average temperature varied by -0.03°C from the base measure. Between which two years should 1946 fall when the years are ordered from coldest to warmest?
Solution: (a) Order of five years from coldest to warmest is 1964, 1965, 1978, 1958, 2002
(b) In 1946, the average temperature varied by -0.03°C.
Since,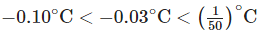
∴ 1946 should fall between 1965 and 1978.
Q.83. In her science class, Jyoti learned that the atomic weight of Helium is 4.0030; of Hydrogen is 1.0080; and of Oxygen is 16.0000. Find the difference between the atomic weights of:
(a) Oxygen and Hydrogen
(b) Oxygen and Helium
(c) Helium and Hydrogen
Solution: Atomic weight of Helium = 4.0030
Atomic weight of Hydrogen = 1.0080
Atomic weight of Oxygen – 16.0000
(a) Difference between the atomic weights of Oxygen and Hydrogen
= 16.0000 – 1.0080
= 14.9920
(b) Difference between atomic weights of Oxygen and Helium = 16.0000 – 4.0030 = 11.9970
(c) Difference between atomic weights of Helium and Hydrogen = 4.0030 – 1.0080 = 2.9950
Q.84. Measurement made in science lab must be as accurate as possible. Ravi measured the length of an iron rod and said it was 19.34 cm long; Kamal said 19.25 cm; and Tabish said 19.27 cm. The correct length was 19.33 cm. How much of error was made by each of the boys?
Solution:
The correct length of the iron rod = 19.33 cm
The length of the rod measured by Ravi = 19.34 cm
∴ Error made by Ravi = (19.34 – 19.33)cm = +0.01 cm
The length of the rod measured by Kamal = 19.25 cm
∴ Error made by Kamal = (19.25 – 19.33) cm = -0.08 cm
The length of the rod measured by Tabish = 19.27 cm
∴ Error made by Tabish = (19.27 – 19.33) cm = -0.06 cm.
Q.85. When 0.02964 is divided by 0.004, what will be the Questionuotient?
Solution: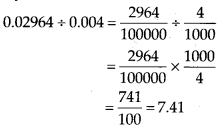
Q.86. What number divided by 520 gives the same Questionuotient as 85 divided by 0.625?
Solution:
Let a number x be divided by 520.
According to question,
x ÷ 520 = 85 ÷ 0.625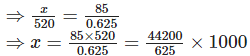
= 70.72 × 1000 = 70720
Thus, the required number is 70720.
Q.87. A floor is 4.5 m long and 3.6 m wide. A 6 cm square tile costs Rs. 23.25. What will be the cost to cover the floor with these tiles?
Solution: Length of the floor = 4.5 m
= (4.5 × 100) cm = 450 cm
Width of the floor – 3.6 m – (3.6 × 100) cm = 360 cm
∴ Area of the floor – (450 × 360) cm2 = 162000 cm2
Side of a square tile = 6 cm
∴ Area of one square tile = (6 × 6) cm2 = 36 cm2
Number of tiles reqnuired to cover the floor
= 4500
Now, cost of one tile = Rs. 23.25
∴ Cost of 4500 tiles =Rs. (23.25 ×4500)
= Rs. 104625
Q.88. Sunita and Rehana want to make dresses for their dolls. Sunita has 3/4 m of cloth, and she gave 1/3 of it to Rehana. How much did Rehana have?
Solution: Length of cloth Sunita has =3/4 m
∴ Length of cloth Rehana has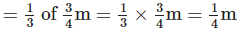
Q.89. A flower garden is 22.50 m long. Sheela wants to make a border along one side using bricks that are 0.25 m long. How many bricks will be needed?
Solution:
Length of the garden = 22.50 m
Length of one brick = 0.25 m
∴ Number of bricks required to make the border =
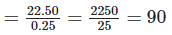
Q.90. How much cloth will be used in making 6 shirts, if each required 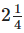 [ m of cloth, allowing
[ m of cloth, allowing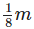 for waste in cutting and finishing in each shirt?
for waste in cutting and finishing in each shirt?
Solution:
Length of cloth required for one shirt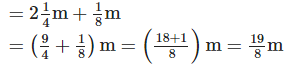
∴ Length of cloth required for 6 shirts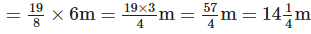
Q.91. A picture hall has seats for 820 persons. At a recent film show, one usher guessed it was 3/4 full, another that it was 2/3 full. The ticket office reported 648 sales. Which usher (first or second) made the better guess?
Solution: Total number of seats = 820
Sale of total tickets = 648
Number of sold tickets guessed by first usher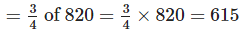
Number of sold tickets guessed by second usher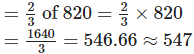
Since, 615 is more close to 648 than 547.
∴ First usher made the better guess.
Q.92. For the celebrating children day, students of Class VII bought sweets for Rs. 740.25 and cold drink for Rs. 70. If 35 students contributed eQuestionually what amount was contributed by each student?
Solution: Total spending amount = Rs.740.25 + Rs.70
= Rs. 3810.25
Total number of students who contributed money = Rs. 35
∴ Contribution of each student = 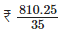
= Rs. 23.15
Q.93. The time taken by Rohan in five different races to run a distance of 500 m was 3.20 minutes, 3.37 minutes, 3.29 minutes, 3.17 minutes and 3.32 minutes. Find the average time taken by him in the races?
Solution: Total time taken by Rohan in five races
= (3.20 +3.37 +3.29 +3.17 +3.32] minutes
= 16.35 minutes
Total number of races = 5
∴ The average time taken by Rohan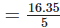 minutes = 3.27 minutes
minutes = 3.27 minutes
Q.94. A public sewer line is being installed along 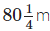 of road. The supervisor says that the labourers will be able to complete 7.5 m in one day. How long will the project take to complete?
of road. The supervisor says that the labourers will be able to complete 7.5 m in one day. How long will the project take to complete?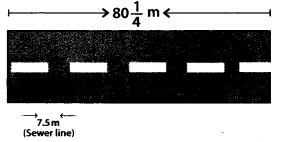
Solution:
Total length of a sewer line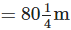
1/7.5 m long sewer line completed in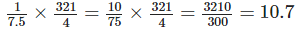
≈ 11 days
Q.95. The weight of an object on moon is 1/6 its weight on Earth.If an object weighs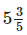 kg on Earth, how much would it weigh on the moon?
kg on Earth, how much would it weigh on the moon?
Solution: Weight of the object on Earth =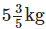
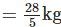
∴ Weight of that object on Moon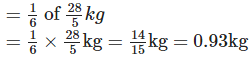
Q.96. In a survey, 200 students were asked what influenced them most to buy their latest CD. The results are shown in the circle graph.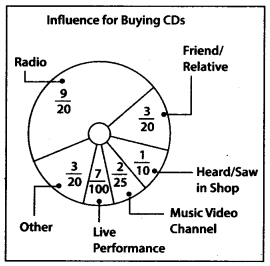
(a) How many students said radio influenced them most?
(b) How many more students were influenced by radio than by a music video channel?
(c) How many said a friend or relative influenced them or they heard the CD in a shop?
Solution: Total number of students = 200
(a) Number of students who were influenced by radio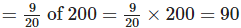
(b) Number of students who were influenced by music video channel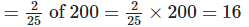
Number of students who were influenced by radio = 90
∴ 90-16-74 more students were influenced by radio than by a music video channel.
(c) Numberofstudents who were influenced by friend or relative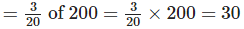
Number of students who were influenced by hearing or seeing the CD in a shop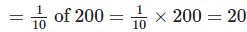
∴Total number of students who were influenced by both friend or relative and hearing the CD in a shop = 30 + 20 – 50
Q.97. In the morning, a milkman filled 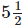 L of milk in his can. He sold to Renu, Kamla and Renuka
L of milk in his can. He sold to Renu, Kamla and Renuka 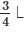 each; to Shadma he sold
each; to Shadma he sold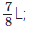 and to Jassi he gave
and to Jassi he gave 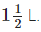 How much milk is left in the can?
How much milk is left in the can?
Solution: Total quantity of milk in the can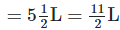
Total quantity of milk to be sold to different persons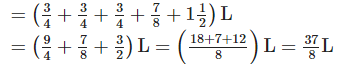
Now, quantity of milk left in the can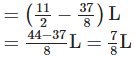
Q.98. Anuradha can do a piece of work in 6 hours. What part of the work can she do in 1 hour, in 5 hours, in 6 hours?
Solution: Let whole work be represented by W.
The part of work done by Anuradha in 6 hours = W
∴ The part of work done by her in 1 hour = W/6
The part of work done by her in 5 hours =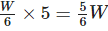
The part of work done by her in 6 hours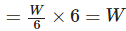
Hence, Anuradha can do 1/6 part of work in 1 hour, 5/6 part of work in 5 hours and complete work in 6 hours.
Q.99. What portion of a ‘saree’can Rehana paint in 1 hour if it requires 5 hours to paint the whole saree? In 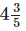 hours? In
hours? In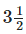 hours?
hours?
Solution:Let total portion of saree be represented by 1.
The portion of saree painted by Rehana in 5 hours = 1.
∴ The portion of saree painted by her in 1 hour = 1/5
The portion of Saree painted by her in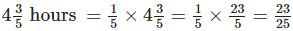
The portion of saree painted by her in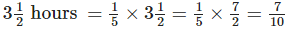
Q.100. Rama has 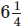 kg of cotton wool for making pillows. If one pillow takes
kg of cotton wool for making pillows. If one pillow takes 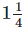 kg, how many pillows can she make?
kg, how many pillows can she make?
Solution: Total quantity of cotton wool = 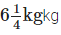
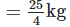
Quantity of cotton wool required for one pillow = 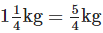
∴ Required number of pillows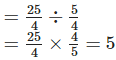
Q.101. It takes 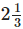 of cloth to make a shirt. How many shirts can Radhika make from a piece of cloth
of cloth to make a shirt. How many shirts can Radhika make from a piece of cloth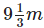 long?
long?
Solution:
Total length of cloth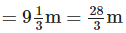
Length of the cloth required for one shirt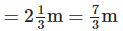 Required number of shirts
Required number of shirts 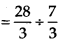
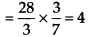
Q.102. Ravi can walk 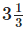 km in one hour. How long will it take him to walk to his office which is 10 km from his home?
km in one hour. How long will it take him to walk to his office which is 10 km from his home?
Solution: Time taken by Ravi to walk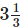 km = 1 hour
km = 1 hour
∴ Time taken by him to walk 1 km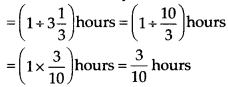
So, time taken by him to walk 10 km
Q.103. Raj travels 360 km on three fifths of his petrol tank. How far would he travel at the same rate with a full tank of petrol?
Solution: Distance travelled by Raj with 3/5 petrol tank = 360 km
Distance travelled by him with a full petrol tank = 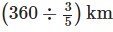
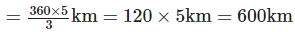
Q.104. Kajol has Rs. 75. This is 3/8 of the amount she earned. How much did she earn?
Solution: Let money earned by Kajol be Rs. x.
According to question,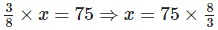
⇒ x = 200
∴ The amount earned by Kajol is Rs. 200.
Q.105. It takes 17 full specific type of trees to make one tonne of paper. If there are 221 such trees in a forest, then
(i) what fraction of forest will be used to make;
(a) 5 tonnes of paper.
(b) 10 tonnes of paper.
(ii) To save 7/13 part of the forest how much of paper we have to save.
Solution: (i) Number of trees required to make one tonne of paper = 17
Total number of trees = 221
∴ Fraction of forest will be used to make one tonne of paper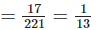
(a) Fraction of forest will be used to make 5 tonnes of paper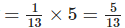
(b) Fraction of forest will be used to make 10 tonnes of paper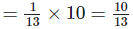
(ii) Let we have to save x tonnes of paper to save 7/13 part of forest
Fraction of forest will be used to make x tonnes of paper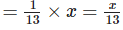
Now,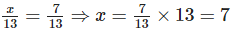
Q.106. Simplify and write the result in decimal form: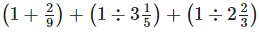
Solution:
Q.107. Some pictures (a) to (f) are given below. Tell which of them show: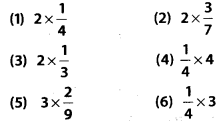
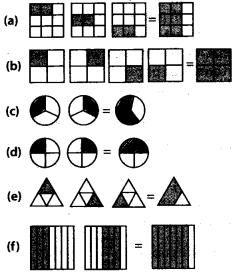
Solution:
1. 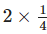 represents the addition of 2 figures, each representing 1 shaded part out of 4 equal parts.
represents the addition of 2 figures, each representing 1 shaded part out of 4 equal parts.
Hence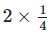 is represented by (d).
is represented by (d).
2.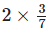 represents the addition of 2 figures, each representing 3 shaded parts out of 7 equal parts.
represents the addition of 2 figures, each representing 3 shaded parts out of 7 equal parts.
Hence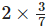 is represented by (f).
is represented by (f).
3. 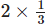 represents the addition of 2 figures, each representing 1 shaded part out of 3 equal parts.
represents the addition of 2 figures, each representing 1 shaded part out of 3 equal parts.
Hence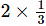 is represented by (c).
is represented by (c).
4. 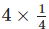 represents the addition of 4figures, each representing 1 shaded part out of 4 equal parts.
represents the addition of 4figures, each representing 1 shaded part out of 4 equal parts.
Hence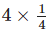 is represented by (b).
is represented by (b).
5. 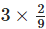 represents the addition of 3 figures, each representing 2 shaded parts out of 9 equal parts.
represents the addition of 3 figures, each representing 2 shaded parts out of 9 equal parts.
Hence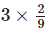 is represented by (a).
is represented by (a).
6. 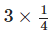 represents the addition of 3 figures, each representing 1 shaded part out of 3 equal parts.
represents the addition of 3 figures, each representing 1 shaded part out of 3 equal parts.
Hence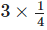 is represented by (e)
is represented by (e)
Q.108. Evaluate : (0.3) × (0.3) – (0.2) (0.2)
Solution: (0.3) × (0.3) – (0.2) ×(0.2)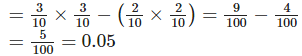
Q.109. Evaluate: 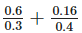
Solution: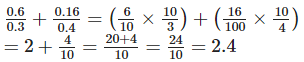
Q.110. Find the value of: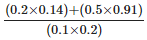
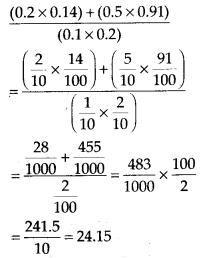
Solution:
Q.111. A square and an equilateral triangle have a side in common. If side of triangle is 4/3 cm long, find the perimeter of figure formed (see figure).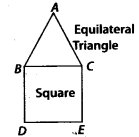
Solution: Side of the equilateral triangle =4/3 cm
∴ Side of the square =4/3 cm
∴ Perimeter of given figure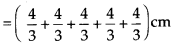
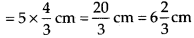
Q.112. Rita has bought a carpet of size 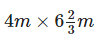 But her room size is
But her room size is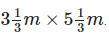 What fraction of area should be cut off to fit wall to wall carpet into the room?
What fraction of area should be cut off to fit wall to wall carpet into the room?
Solution: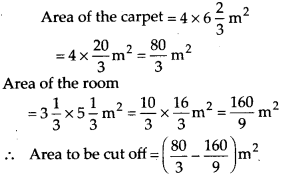
=8.88 m2
Q.113. Family photograph has length 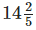 cm and breadth
cm and breadth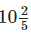 cm.It has border of uniform width
cm.It has border of uniform width 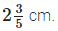 Find the area of framed photograph.
Find the area of framed photograph.
Solution: Length of photograph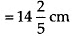
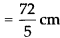
Breadth of photograph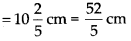
Width of border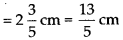
Length of framed photograph
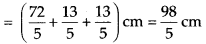
Breadth of framed photograph
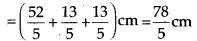
Area of framed photograph
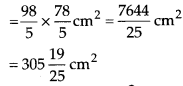
Q.114. Cost of a burger is 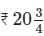 and of Macpuff is
and of Macpuff is 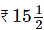 Find the cost of 4 burgers and 14 macpuffs.
Find the cost of 4 burgers and 14 macpuffs.
Solution:
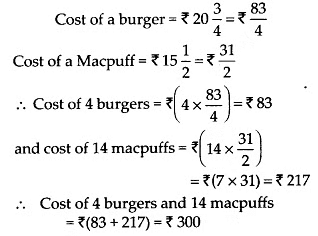
Q.115. A hill,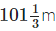 in height, has 1/4th of its height under water. What is the height of the hill visible above the water?
in height, has 1/4th of its height under water. What is the height of the hill visible above the water?
Solution: Total height of the hill
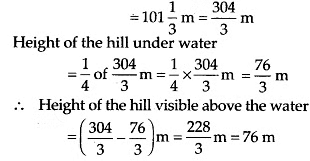
Q.116. Sports: Reaction time measures how Questionuickly a runner reacts to the starter pistol. In the 100 m dash at the 2004 Olympic Games, Lauryn Williams had a reaction time of 0.214 second. Her total race time, including reaction time, was 11.03 seconds. How long did it take her to run the actual distance?
Solution: Total race time of Lauryn Williams = 11.03 seconds
Her reaction time = 0.214 second
∴ Time taken by her to run the actual distance
=(11.03 – 0.214) seconds = 10.816 seconds
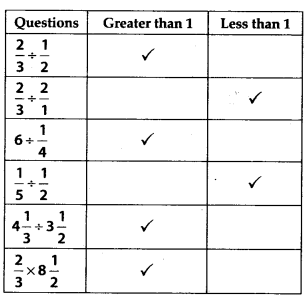
Q.117. State whether the answer is greater than 1 or less than 1. Put a’mark in appropriate box.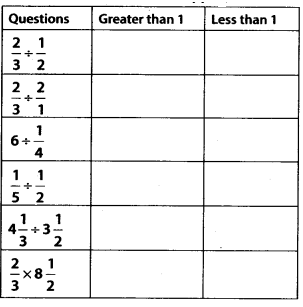
Solution:
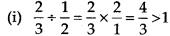
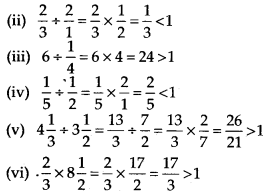
Q.118. There are four containers that are arranged in the ascending order of their heights. If the height of the smallest container given in the figure is expressed as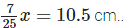 Find the height of the largest container.
Find the height of the largest container.
Solution: Height of the smallest container = 10.5 cm
We have given that
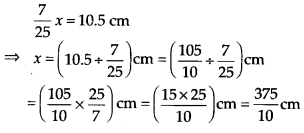
∴ Height of the largest container is 37.5 cm.
Q.119.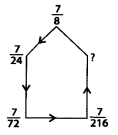
Solution:
Here, the pattern is
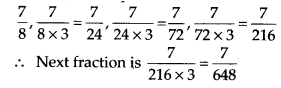
Q.120.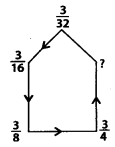
Solution:
Here, the pattern is
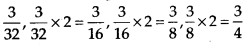

Q.121.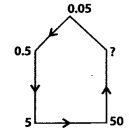
Solution:
Here, the pattern is 0.05, 0.05 × 10 – 0.5, 0.5 × 10 – 5,5 × 10 = 50
∴ Next number will be 50 × 10 = 500
Q.122.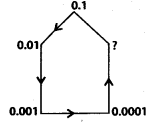
Solution:
Here, the pattern is
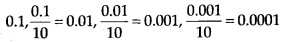
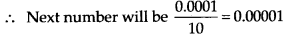
Q.123. A student compared 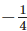 and -0.3. He changed
and -0.3. He changed 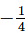 to the decimal -0.25 and wrote, “Since 0.3 is greater than 0.25,-0.3 is greater than -0.25”. What was the student’s error?
to the decimal -0.25 and wrote, “Since 0.3 is greater than 0.25,-0.3 is greater than -0.25”. What was the student’s error?
Solution: Since 0.3 is greater than 0.25.
∴ -0.3 is less than -0.25
∴ The error is -0.30 >-0.25
Q.124. A student multiplied two mixed fractions in the following manner: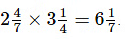 What error the student has done?
What error the student has done?
Solution:
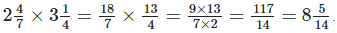
but given that
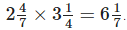
∴ Error is that mixed fractions are not converted into improper fractions.
Q.125. In the pattern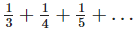 which fraction makes the sum greater than 1 (first time)? Explain.
which fraction makes the sum greater than 1 (first time)? Explain.
Solution:
|
76 videos|452 docs|39 tests
|
FAQs on NCERT Exemplar Solutions: Fractions & Decimals - Mathematics (Maths) Class 7 (Old NCERT)
| 1. How do you add fractions with different denominators? |  |
| 2. How do you subtract fractions with different denominators? |  |
| 3. How do you simplify a fraction? |  |
| 4. How do you convert a fraction to a decimal? |  |
| 5. How do you convert a decimal to a fraction? |  |

















