Triangles Class 9 Worksheet Maths Chapter 6
Multiple Choice Questions
Q1: If AD = BC and ∠ BAD = ∠ ABC, then ∠ ACB is equal to
(a) ∠ABD
(b) ∠ BAD
(c) ∠BAC
(d) ∠BDA
Ans: (d)
In △ABC and △ABD
AD =BC (given)
∠ BAD = ∠ ABC (Given)
AB = AB (Common side)
∴ △ABC ≅ △ABD
By CPCT theorem, ∠ACB=∠BDA ( By SAS Congruency)
Q2: If O is a midpoint of AB and ∠BQO = ∠APO, then ∠OAP is equal to
(a) ∠QPA
(b) ∠OQB
(c) ∠QBO
(d) ∠BOQ
Ans: (c)
In △AOP and △BOQ
AO = BO….. (O is the midpoint of AB)
∠APO = ∠BQO (Given)
∠AOP = ∠BOQ (Vertically opposite Angles)
∴△AOP ≅ △BOQ (By AAS Congruency)
By CPCT ∠OAP = ∠QBO
Q3: If △ABC is an isosceles triangle, AB = AC,∠ B = 65º, then find ∠ A.
(a) 60º
(b) 70º
(c) 50º
(d) none of these
Ans: (c)
Since △ABC is on an isosceles triangle
∴ ∠B = ∠C
∴ ∠B = 65º
∴ ∠C = 65º
∴ ∠A+∠B +∠C = 180º
∴ ∠A + 130º = 180º
∴ ∠A = 180º − 130º
∴∠A = 50º
Q4: An angle is 14º more than its complement. Find its measure.
(a) 42
(b) 32
(c) 52
(d) 62
Ans: (c)
Two angles whose sum equals 90 degrees are called complementary angles.
let first angle = x
it’s Complement = 90º − x
According to the question,
x = 14º + 90º − x
x = 104º − x
⇒ 2x = 104º
⇒ x = 104º/2
∴ x = 52º
Q5: If ABCD is a quadrilateral where AD = CB, AB = CD, and ∠ D = ∠ B, then ∠CAB is equal to
(a) ∠ACD
(b) ∠CAD
(c) ∠ACD
(d) ∠BAD
Ans: (c)
In △ABC and △CDA
CB = AD (Given)
AB = CD (Given)
∠B = ∠D (Given)
∴△ABC ≅ △CDA (By SAS Congruency)
By CPCT theorem
∠CAB = ∠ACD
Q6: If AB ⊥BC and ∠A =∠C, then the correct statement will
(a) AB ≠ AC
(b) AB = BC
(c) AB = AD
(d) AB = AC
Ans: (b)
In △ABC, ∠A = ∠C
Opposite sides to equal angles are also equal
AB = BC
Q7: If AB = AC and ∠ BAC = 120°, find ∠A.
(a) 50°
(b) 60°
(c) 70°
(d) none of these
Ans: (b)
Given- AB = AC
Therefore, ∠ABC = ∠ACB;
Let, ∠ABC = x = ∠ACB;
In ΔABC
∠A + ∠B + ∠C = 180° (sum of all angles of a triangle is 180°)
120° + x + x = 180°
2x = 180° - 120°
x = 60° / 2 = 30°, then, ∠B = ∠C = 30°
Answer the following questions
Q1: AD and BC are equal perpendiculars to a line segment AB. Show that CD bisects AB.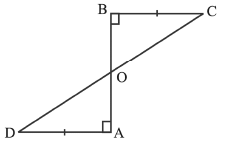
Ans: In ΔAOD and ΔBOC,
BC = AD given
∠OAD = ∠OBC (90 º)
Since, BC || AD
∠ODA = ∠OCB (alternate angles are equal)
So, ΔAOD ≅ ΔBOC (by the ASA congruence rule)
OD = OC (CPCT)
AO = OB (CPCT)
Therefore, CD bisects AB.
Q2: AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠BAD = ∠ABE and ∠EPA = ∠DPB. Show that
(i) ΔDAP ≌ ΔEBP
(ii) AD = BE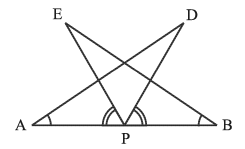 Ans. (i) ΔIn DAP and ΔEBP
Ans. (i) ΔIn DAP and ΔEBP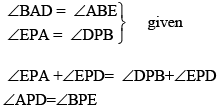
P is its mid-point of AB
∴ AP = PB
So, ΔDAP ≌ ΔEBP(by the ASA congruence rule)
(ii) AD = BE(CPCT)
Q3: In an isosceles triangle ABC with AB = AC, D and E are points on BC such that BE = CD. Show that AD = AE.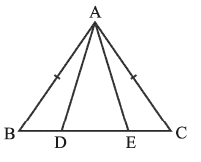 Ans: In ΔABD and ΔACE,
Ans: In ΔABD and ΔACE,
AB = AC (Given) ..(1)
∠B = ∠C (Angles opposite to equal sides) ..(2)
Also, BE = CD..(3)
So, BE – DE = CD – DE
That is, BD = CE (3)
So, ΔABD ≌ ΔACE by SAS rule
(Using (1), (2), (3) and SAS rule).
This gives AD = AE (CPCT)
Q4: In Figure OA = OB and OD = OC.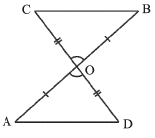 Show that
Show that
(i) ΔAOD ≅ ΔBOC
(ii) AD || BC
Ans: (i) In ΔAOD and ΔBOC,
OA = OB (given)
OD = OC (given)
∠AOD = ∠BOC (pair of vertically opposite angles)
So, ΔAOD ≅ ΔBOC(by the SAS congruence rule)
(ii) ∠OAD = ∠OBC (CPCT)
and these form a pair of alternate angles for line segments AD and BC.
Therefore, AD || BC.
Q5: In Fig, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.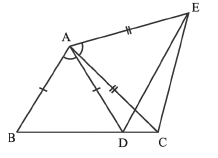
Ans. In ΔABC and ΔADE,
AB = AD (given)
AC = AE (given)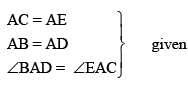
∠ADC+ ∠BAD = ∠ADC + ∠EAC
∠BAC = ∠DAE
So, ΔABC ≌ ΔADE (by the SAS congruence rule)
BC = DE (CPCT)
Q6: In ΔABC, the bisector AD of ∠A is perpendicular to side BC. Show that AB = AC and ΔABC is isosceles.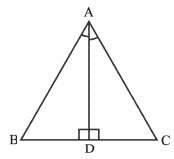 Ans: In ΔABD and ΔADC
Ans: In ΔABD and ΔADC
AD bisects ∠A
⇒ ∠BAD = ∠CAD
∠ADC = ∠ADB 90º
AD = AD (Common Side)
So, ΔABD ≌ ΔADC (by the SAS congruence rule)
AB = AC(CPCT)
∴ ΔABC is isosceles
Q7: ABC is a triangle in which altitudes BE and CF to sides AC and AB are equal. Show that
(i) ΔABE ≌ ΔACF
(ii) AB = AC, i.e., ABC is an isosceles triangle.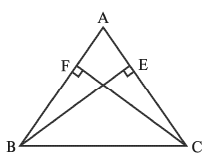 Ans: In ΔABE and ΔACF,
Ans: In ΔABE and ΔACF,
BE = FC (Given) ..(1)
∠A = ∠A (Common Angle) ..(2)
Also, ∠ABE = ∠ACF ....(3)
So, ΔABE ≌ ΔACF (Using (1), (2), (3) and ASA rule).
This gives AB = AC (CPCT)
∴ ABC is an isosceles triangle
|
40 videos|566 docs|57 tests
|
FAQs on Triangles Class 9 Worksheet Maths Chapter 6
| 1. What are the different types of triangles based on their sides? |  |
| 2. How do you calculate the area of a triangle? |  |
| 3. What is the Pythagorean theorem, and how does it relate to triangles? |  |
| 4. Can triangles be similar, and how can you determine if two triangles are similar? |  |
| 5. What is the significance of the triangle inequality theorem? |  |
















