Summary & Examples: Number Series | Logical Reasoning (LR) and Data Interpretation (DI) - CAT PDF Download
Number Series is an important topic in competitive exams, with a specific focus as five questions are dedicated solely to this section. It holds significant importance in various exams. Candidates preparing for competitive exams can secure 4-5 marks in just 2-3 minutes by understanding the different types and patterns of number series in both reasoning and quantitative aptitude.
What is Number Series?
- Number series is a form of sequence, where some numbers are mistakenly put into the series of numbers and some number is missing in that series, we need to observe first and then find the accurate number to that series.
- The questions can also be where you are supposed to determine a continuation to they series or the immediate next term of the series.
- The sequence is the list of numbers written in a specific order.
Common Types of Number Series

Type 1: Addition / Subtraction or Multiplication / Division
These series follow the pattern of addition or subtraction of even or odd numbers.
Example 1: What should come in place of the question mark in the following series: 19, 23, 39, 75, ?, 239.
- The most common trick to solve a number series is to solve by checking the difference between two adjacent numbers, but the difference could not only lead to addition/subtraction but it can also be with multiplication/division.
- Therefore, to check whether to think addition-wise or multiplication-wise in increasing sequence, one must assume with the help of the difference between the first and last number of the given sequence.
- If the difference seems to be less according to the number of steps used to make the last number from first than we should check addition.
- If the difference seems to be large or too large one must check the multiplication trick between the adjacent numbers.
In Example 1, given above, the difference between first no. (19) and last number (239) is 220.
- Now a question will arise how we will assume whether the difference is more or less. We will assume it by keeping in mind the number of steps required to start from the first number till the last number.
- In Example 1, 19 becomes 239 in five steps, because there are four more numbers between them, one of which we have to find out.
- The difference of 220 between 19 and 239 in five steps logically giving priority to addition over multiplication in an increasing sequence like this.

- 75 + 64 = 139, 139 + 100 = 239
139 is the correct answer.
Example 2: What should come in place of question mark in the following series: 10, 31, 95, 288, ?, 2609.
As we can see in the above example, the difference between the first number (10) and the last number (2609) is 2599 in five steps, which indicate us to check multiplication trick between the numbers.
(288*3) + 4 = 868, is the correct answer.
Note : While checking multiplication trick always start from right end of the sequence.
Example 3: What should come in place of question mark in the following series:
30, 34, 43, 59, 84, 120, ?.
(a) 169
(b) 148
(c) 153
(d) 176
(e) None of these
Correct Answer is Option (a)
The given pattern is:+4, +9, +16, +25 and so on.
So, missing term is 169 = 120 + 49
Example 4: What should come in place of question mark in the following series:
40, 54, 82, ?, 180, 250.
(a) 142
(b) 124
(c) 136
(d) 163
(e) None of these
Correct Answer is Option (c)
The pattern is: +14, + 28, + 42, + 56, + 70
So, missing term is 82 + 42 = 124
Example 5: Find the wrong number in the below-mentioned series:
0, 1, 3, 8, 18, 35, 264
(a) 62
(b) 35
(c) 18
(d) 8
(e) None of these
Correct Answer is Option (a)
There is a pattern in difference between the consecutive numbers:
0 - 1 = 1 ← 02 + 1
1 - 3 = 2 ← 12 + 1
3 - 8 = 5 ← 22 + 1
8 - 18 = 10 ← 32 + 1
18 - 35 = 17 ← 42 + 1
Next difference should be 52 + 1 i.e. 26.
35 - 61 = 26 ← 52 + 1
From above the correct sequence would be: 0, 1, 3, 8, 18, 35, 61 and
so, the wrong number is: 264
Example 6: Find the wrong number in the below-mentioned series:
5531, 5506, 5425, 5304, 5135, 4910, 4621
(a) 5531
(b) 5425
(c) 4621
(d) 5135
(e) 5506
Correct Answer is Option (a)
The number should be 5555 in place of 5531.
-72, -92, -112, -132, -152, -172…
Example 7: Find the wrong number in the below-mentioned series:
6, 7, 9, 13, 26, 37, 69
(a) 7
(b) 26
(c) 69
(d) 37
(e) 9
Correct Answer is Option (b)
The number should be 21 in place of 26.
The pattern is: +1, +2, +4, +8, +16, +32
Example 8: Find the wrong number in the below-mentioned series:
1, 3, 10, 36, 152, 760, 4632
(a) 3
(b) 36
(c) 4632
(d) 760
(e) 152
Correct Answer is Option (d)
The number should be 770 in place of 760.
The pattern is: ×1 +2, ×2 +4, ×3 +6, ×4 + 8, ×5 +10, ×6 + 12, …
Type 2: Perfect Square or Perfect Cube
Question: 4, 18, 48, 100, 180, ___.
- In case, if Type-1 is not applicable in a sequence, then in the next step, we must compare given numbers or their differences to square or cube of natural numbers, as in the above example.

- Therefore, (7)3-(7)2 = 294, is the correct answer.
(a) Perfect Square Series:
This type of series is based on the square of a number that is in the same order and one square number is missing in that given series.
Example 11: In the following options, a few number series are present. One of them has an error, pick the wrong one out:
(a) 3, 9, 15, 21
(b) 9, 81, 225, 441
(c) 441, 529, 676, 841
(d) 900, 841, 784, 729
Answer: (c)
Solution: The first series is just an A.P. with a common difference of 6. Now, we can see that the second sequence is the perfect square sequence. This series can be formed from the series given in option A. The third sequence is a two-tier square series but in place of 841, we must have 900. This is the wrong series. The last series is also a square series. So the correct option or the wrong series of the four options presented above is C) 441, 529, 676, 841.
Example 12: What should come in place of question mark in the following series:
841, ?, 2401, 3481, 4761
Answer: These numbers are squares of certain integers:
292, 392, 492, 592, 692
The missing number, therefore, is 392 = 1521.
8, 12, 21, 37, __
Example 13: What should come in place of question mark in the following series:
1, 9, 25, ?, 81, 121
Answer: 12, 32, 52, 72, 92, 112
The missing number is 49.
Example 14: What should come in place of question mark in the following series:
289, 225, 169, ?, 81
Answer: 172, 152, 132, 112, 92
The missing number is 121.
(b) Perfect Cube Series:
This type of series is based on the cube of a number that is in the same order and one cube number is missing in that given series.
Example 15: What should come in place of question mark in the following series:
3375, ?, 24389, 46656, 79507
Answer: 153, 223, 293, 363, 433
(Each cube digit added with seven to become next cube number)
The missing number is 10648.
Example 16: What should come in place of question mark in the following series:
729, 6859, 24389, ?, 117649, 205379
Answer: 93, 193, 293, 393, 493, 593
The missing number is 59319.
Example 17: What should come in place of question mark in the following series:
1000, 8000, 27000, 64000, ?
Answer: 103, 203, 303, 403, 503
The missing number is 125000.
Type 3: Factorisation / Prime Factorisation
- If Type 1 and Type 2 is not applicable in a sequence, one must try to make factors of the numbers in the next step.
Example 18: 6, 15, 35, 77, 143, __.
In the above example, all the previous tricks are not applicable to get an answer. Hence, We will make factors of the given numbers. (2,3,5,7,11,13) all are prime numbers in ascending order.
(2,3,5,7,11,13) all are prime numbers in ascending order.
Hence, 13*17 = 221, is the correct answer.
Type 4: Fibonacci Series
- A series in which a number is made by using previous two numbers are called Fibonacci series.
Example 19: 1, 4, 5, 9, 14, 23, ___
In the above sequence, all the numbers are the sum of the previous two numbers.
Therefore, 23+14 = 37, is the correct answer.
Type 5: Sum of Digits
Example 20: In the above sequence, the difference between two numbers is the sum of the digits of the first number.
In the above sequence, the difference between two numbers is the sum of the digits of the first number.
Hence, 89+17 = 106, is the correct answer.
Example 21: 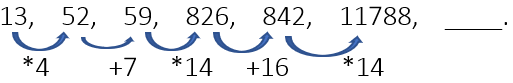 All the numbers are multiplied by their sum or added by their sum alternately.
All the numbers are multiplied by their sum or added by their sum alternately.
Therefore, 11788 + 25 = 11813, is the correct answer.
Type 6: Alternate Pattern Series
- When numbers given as a hint in a question are more or when a question asks two numbers of a series or the same number come twice in a series, these all give a hint to alternate pattern series.
Example 22:  So, numbers are 12+5 = 17, 53-6 = 47
So, numbers are 12+5 = 17, 53-6 = 47
Ans. 17, 47
Example 23: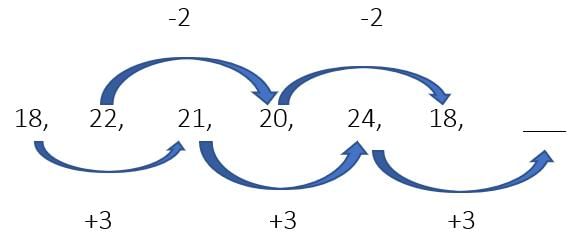
So, the number is 24+3 = 27
Ans. 27
Type 7: Decimal Pattern Series
When the numbers of the sequence are given in the decimal form is decimal pattern series.
Example 24:  So, the answer is 18 * 0.8 = 14.4
So, the answer is 18 * 0.8 = 14.4
Example 25: 16, 24, 60, 210, 945, __
The pattern is:
16 x 1.5 = 24
24 x 2.5 =60
60 x 3.5 = 210
210 x 4.5 = 945
945 x 5.5 = 5197.5
Type 8: Bracket Pattern Series
While using bracket pattern we multiply first outside and either add or sub based on given number.
Example 26: 3, 28, 180, ____, 3676
The pattern is :
(3+1)x7 = 28
(28+2)x6 =180
(180+3)x5 = 915
(915+4)x4 = 3676
Ans. 915
Example 27: 37, 31, 52, 144, __, 2810
The pattern is :
(37-6)x1=31
(31-5)x2=52
(52-4)x3=144
(144-3)x4=564
(564-2)x5=2810
Ans. 564
Type 9: Dual Pattern Series
Example 28:
15, 9, 8, 12, 36, 170
19, a, b, __, d, e,
The pattern is :
(15-6)x1=9
(9-5)x2=8
(8-4)x3=12
Similarly:
(19-6)x1=13
(13-5)x2=16
(16-4)x3=36
Ans. 36
Type 10: Factorial Based Series
This is the latest pattern question asked in the latest exams.
Example 29: 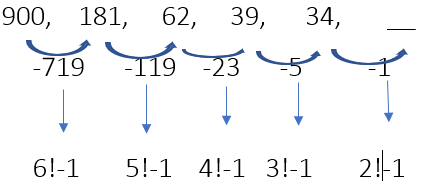 Ans. 33
Ans. 33
Example 30: 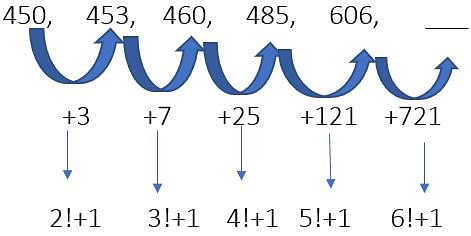 Ans. 606 + 721 = 1327
Ans. 606 + 721 = 1327
Type 11: Arithmetic Series
A series in which the next term is obtained by adding or subtracting a constant number to its previous term.
Example 1: Find the next term 7, 12, 17, 22, 27, ?
Solution:
The above series is an Arithmetic series where 5 is added to each term to get the next term i.e.
- 12 = 7 + 5
- 17 = 12 + 5
- 22 = 17 + 5
- 27 = 22 + 5
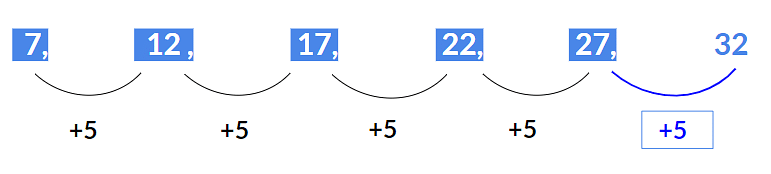 Hence next term will be 27 + 5 = 32.
Hence next term will be 27 + 5 = 32.
Example 2: Write the missing term 29, 23, 17, 11, ?
Solution:
The above series is an Arithmetic series where 6 is subtracted from each term to get the next term i.e.
- 29 – 6 = 23
- 23 – 6 = 17
- 17 – 6 = 11
Hence next term will be 11 - 6 = 5.
Type 11: Geometric Series
A series where each successive number is obtained by either multiplying or dividing the previous number by a specific number.
Example 1: Find the missing term 3, 12, 48, 192, ?
Solution:
Here each number is multiplied by 4 to get the next number i.e.
- 12 = 3 x 4
- 48 = 12 x 4
- 192 = 48 x 4
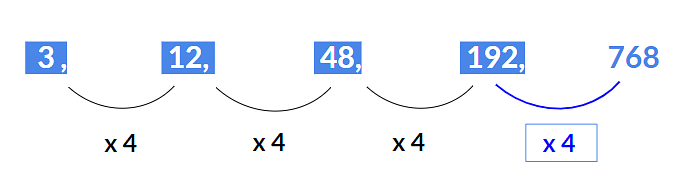 Hence next term will be 192 x 4 = 768.
Hence next term will be 192 x 4 = 768.
Example 2: Find the next term 729, 243, 81, 27, ?
Solution.
Here each number is divided by 3 to get the next number.
- 729/3 = 243
- 243/3 = 81
- 81/3 = 27
Hence next term will be 27/3 = 9
Type 12: Mixed Series
A series where more than one pattern is arranged in a single series.Example 1: Find the missing term 2, 8, 26, 80, 242, ?
Solution:
Here the pattern is (x 3 + 2).
- 2 x 3 + 2 = 8
- 8 x 3 + 2 = 26
- 26 x 3 + 2 = 80
- 80 x 3 + 2 = 242
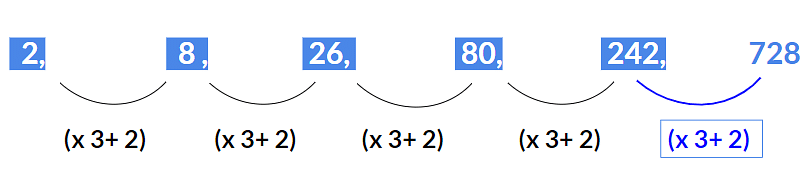 Hence missing term will be242 x 3 + 2 = 728
Hence missing term will be242 x 3 + 2 = 728
Example 2: Find the next term 5, 12, 27, 59, ?
Solution:
Here each term is multiplied by 2 and consecutive prime numbers are added.
- 5 x 2 + 2 = 12
- 12 x 2 + 3 = 27
- 27 x 2 + 5 = 59
Hence next term will be 59 x 2 + 7 = 125
Type 13: Arithmetic – Geometric Series
A series which is a combination of Arithmetic and Geometric series.
Example: Find the next term 3, 5, 10, 12, 24, 26, ?
Solution:
Here the pattern is (+ 2, x 2, + 2, x 2 …..)
- 3 + 2 = 5
- 5 x 2 = 10
- 10 + 2 = 12
- 12 x 2 = 24
- 24 + 2 = 26
Hence the next term will be 26 x 2 = 52
Type 14: Alternate Series
A series where two series is combined into a single series.
Example 1: Find the next term 2, 3, 5, 8, 8, 13, 11, ?
Solution:
► Here alternate terms starting with 2 forms an Arithmetic series with a common difference as 3. (2, 5, 8, 11)
► Also, alternate terms starting with 3 forms another Arithmetic series with a common difference as 5. ( 3, 8, 13,..)
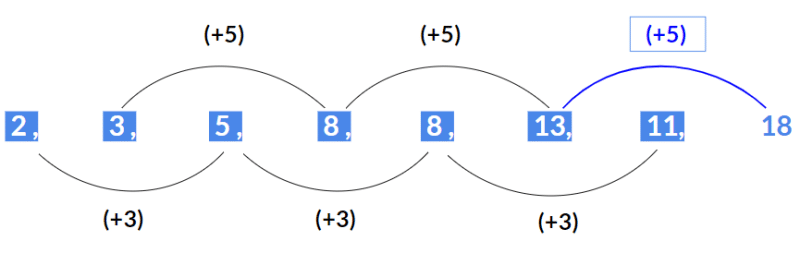 Hence next term will be 18.
Hence next term will be 18.
Example 2: Find the next term 3, 5, 7, 10, 11, 15, 15, ?
Solution:
Here alternate terms starting with 3 forms an Arithmetic series with a common difference as 4. (3, 7, 11, 15)
Also, alternate terms starting with 5 forms a Geometric series with a common ratio as 2. (5, 10, 15)
Hence next term will be 20.
Important Points to Remember
1. If the change is slow or gradual, then it is a difference series.
e.g.

2. If the change is equally sharp, then it is ratio series.
e.g.

3. If the rise is sharp initially, but slows down later, then it is formed by adding squared, or cubed numbers.
e.g.

4. If the series is alternating, then it may be either a mixed series or two different operations going on alternately.
e.g.

|
92 videos|123 docs|94 tests
|
FAQs on Summary & Examples: Number Series - Logical Reasoning (LR) and Data Interpretation (DI) - CAT
| 1. What are the different types of number series? |  |
| 2. How do you identify an addition or subtraction series? |  |
| 3. What is the Fibonacci series, and how is it generated? |  |
| 4. How can perfect squares or cubes be identified in a number series? |  |
| 5. What is an alternate pattern series, and how does it work? |  |

























