Voltage Regulation of Single Phase Transformers
(Refer Slide Time: 00:59)
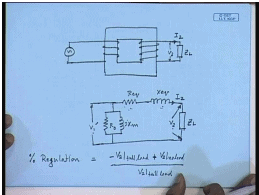
A single phase transformer like this is supplied from a constant voltage constant frequency source from the primary side and connected to the load on the secondary side. In most cases the load would like to see the constant voltage appearing across it independent of the load current I 2; however, in a practical transformer it is usually not the case. By itself there will be some variation in the load voltage depending on the load current. This can be predicted from the approximate equivalent circuit which we draw referred to the load side now; that is the result R e q X e q, the magnetizing branch, applied voltage referred to the load side V 1 dash. This is the load impedance Z L, the load voltage V 2, this is the load current I 2.
Obviously, V 2 dashed is not same as V 1 dashed for all values of load current. This is due to the drop in the series impedances; it will also depend not only on the magnitude of I 2, it will also depend on the phase angle of I 2 with respect to V 2. Now one important performance parameter of a single phase transformer is its voltage regulation which is a measure of the variation in the load voltage with variation of the load; that is percentage regulation, full load percentage regulation of a single phase transformer is defined as V 2 at full load minus V 2 at no load divided by V 2 at full load, or that is V 2 at no load minus V 2 at full load divided by V 2 at full load.
That is how much the output voltage varies as a percentage of its weighted voltage from no load to full load. This is called the percentage regulation of a single phase transformer, and it is a very important performance parameter for a single phase transformer, because this indicates how constant the voltage will be as the load varies. Now from the approximate equivalent circuit it is simple to calculate this percentage regulation; since, we see that the voltage drop is entirely due to the series impedance in order to calculate percentage regulation we can neglect the shunt branch.
(Refer Slide Time: 06:00)
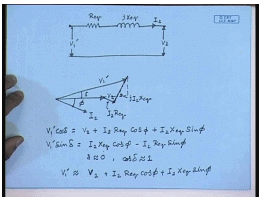
Therefore, the equivalent circuit for calculating percentage impedance will be R e q and j X e q; the applied voltage is V 1 dash, the load voltage is V 2, the current is I 2. Let us draw the phasor diagram, say, this is the load voltage V 2, load current I 2 at a power factor angle of phi. We can draw the phasor of V 1 by noting that V 1 equal to V 2 plus I 2 R e q plus j X e q. This is I 2 R e q, this is j I 2 X e q, this is V 1 dash; therefore, one can write V 1 dash cos delta is equal to V 2 plus I 2 R e q cos phi plus I 2 X e q sine phi and V 1 dash sine delta equal to.
From the previous examples we have seen that the values of R e q and X e q are very small; in the percentage or per unit term they are around 7 percent, 2 percent. So, the quantity V 1 dashed sine delta, the angle delta is usually very close to 0 for a normal transformer even at full load. Therefore, V 1 dashed cos phi cos delta is almost cos delta is approximately equal to 1; hence, V 1 dashed is approximately equal to V 2 plus I 2 R e q cos phi plus I 2 X e q sine phi.
(Refer Slide Time: 10:15)

However, so at a load current I 2 the load voltage V 2 is given by V 2 is approximately equal to V 1 dash minus I 2 R e q cos phi minus I 2 X e q sine phi, obviously, at no load. So, this is V 2 at load, and V 2 no load is obtained by putting I 2 equal to 0 here. So, this is V 1 dash. Hence percentage regulation is defined as V 2 no load minus V 2 at load divided by V 2 at load but V 2 no load equal to V 1 dash; therefore, percentage regulation equal to V 1 dash minus V 1 dash minus I 2 dashed R e q cos phi minus I 2 dashed X e q sine phi divided by V 2 at load or percentage regulation into 100 because of the percentage.
(Refer Slide Time: 12:54)
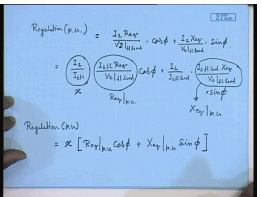
So, the per unit regulation per unit expressed as per unit of rated voltage is equal to I 2 R e q by V 2 at full load into cos phi plus I 2 X e q by V 2 at full load into sine phi. This can be written as this is equal to I 2 divided by I 2 at full load into I 2 full load R e q by V 2 full load cos phi plus I 2 by I 2 full load into I 2 full load X e q divided by V 2 full load sine phi; however, this quantity has earlier been defined as the per unit load x. This quantity has been defined as R e q per unit there, and this quantity has been defined as X e q per unit.
Hence, the per unit regulation can be written as at any fractional loading x is equal to x into R e q per unit into cos phi plus X e q per unit sine phi where the angle phase angle phi is assumed to be positive if the load is lagging, and it is assumed to be negative if it is leading from this expression. So, this is the general expression of per unit regulation; for lagging load phi is assumed to be positive; for leading load phi is assumed to be negative. So, it is operative that percentage regulation can be 0 at leading load. So, at what value of cos phi the percentage regulation is 0?
(Refer Slide Time: 17:03)

So, for zero percentage regulation zero regulation we should have phi equal to X e q sine phi or tan phi equal to or the phase angle at which percentage regulation will be 0 equal to tan phi tan inverse R e q per unit by X e q per unit. This is leading; this is the leading angle. So, at this value of leading phase angle the percentage regulation will be 0; that is at this leading phase angle the percentage regulation at any load, percentage regulation at any load will be 0. So, the terminal voltage under load condition will be same as the no load voltage, and if the phase angle leading phase angle is larger than this then the percentage regulation will be negative, because this term will be larger than this which means physically this will mean under load condition the terminal voltage will be larger than the no load voltage.
So, this is a condition against which we must guard, because the equipment connected to the transformer will in that case see a voltage which is even larger than the no load voltage, and it may damage the equipment. Similarly it will be interesting to find out at what load power factor angle the percentage regulation is maximum; this is obtained by differentiating the expression. So, for maximum percentage regulation we will have d d phi of cos phi plus X e q per unit d d phi of sine phi should be equal to 0, or X e q cos phi should be equal to R e q sine phi, or tan phi again equal to X e q by R e q or phi equal to tan inverse X e q by R e q, but this is lagging.
(Refer Slide Time: 21:16)
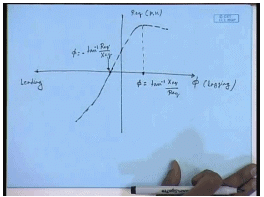
So, if you draw the percentage regulation versus phi this is the lagging direction; this is the leading direction. Please note that at unity power factor percentage regulation is not 0; it is some positive. It is 0 at some leading power factor; let us say at this power factor. This value of phi is equal to we have found this value of phi to be tan inverse R e q by X e q. Similarly, there is a power factor phi the leading zone where the regulation is maximum is this value. So, the percentage regulation if you draw appears somewhat like this. At this point it is maximum at this point it is 0.
This value of phi equal to tan inverse X e q by R e q, and this value of phi equal to minus tan inverse R e q by X e q. This is how the percentage regulation of a transformer which is a measure of how much the output voltage varies depending on the load current can be plotted against load power factor angle. And of course, it is proportional at any given power factor angle it is proportional to the percentage loading. Now let us look at a problem of how to find out the percentage regulation and the output voltage of a transformer.
(Refer Slide Time: 23:50)

Let us consider an 11 kV by 44 volt single phase transformer 50 hertz 11 kV by 440 volt single phase transformer. This transformer from the short circuit test data and 75 kV. A short circuit test data gave the applied voltage V sc equal to 310 volts, I sc equal to 11 ampere, and W sc equal to 1.6 kilowatt. In order to find out percentage regulation we need the series equivalence resistance and the reactance; these are obtained as first we find out Z sc. Zs c equal to V sc by this.
This is rated current that is not 11 ampere; this is 11 kV 75 KVA by 11 kV V sc by I sc is equal to 310 volts divided by I sc which is 45.47 ohm. I R e q, therefore, equal to W sc divided by I sc square which is 1.6 into 10 to the power 3 into 11 square divided by 75 square. This comes to 34.42 ohm. X e q equal to Z sc square minus R e q square and comes to 29.71 ohm. Now we have to convert them to per unit values. So, referred to the short circuit test is done on the HV side. So, V base equal to 11 kV and KVA base of course, is equal to 75 KVA.
(Refer Slide Time: 28:46)

Therefore, R e q per unit equal to 34.42 into KVA base divided by voltage base square. This gives 0.0213. X e q per unit equal to 29.71 into KVA base into 75 KVA divided by 11 kV square 0.0184, and cos phi let us say this transformer is loaded at load with a power factor angle of 0.8 lagging, and at half load that is x equal to 0.5. So, regulation per unit p. u should be equal to x into R e q cos phi plus X e q per unit X e q sine phi equal to 0.5 into 0.0213 into 0.8 plus 0.0184 into 0.6. This then comes to 0.01404. So, percentage regulation equal to 1.404 percent.
(Refer Slide Time: 31:55)

Which means the 1.40 percentage regulation is by definition V 2 at no load minus V 2 at load divided by V 2 at full load. So, V 2 at load will be V 2 at no load minus V 2 at full load into percentage regulation. Now V 2 at no load is given as 440 volts; V 2 at full load at the same power factor can be obtained from the same formula into 0.01404; however, it is not necessary, because this is multiplied by a very small factor. So, changing V 2 at full load actually will be given by V 2 at no load minus V 2 drop, but the magnitude of V 2 drop is much smaller compared to V 2 at no load. And when it is multiplied by this regulation this becomes even smaller; therefore, in all practical purpose these can be assumed to be equal to this.
So, V 2 at load equal to 440 into 1 minus 0.01404. So, this is how from the percentage regulation the given short circuit test data the percentage regulation of a single phase transformer can be found, and with that we can also find what will be the output voltage at any given load. So, far we have seen that most of the parameters equivalent circuit parameters and performance parameters of a single phase transformer can be found from short circuit and no load test data, and we have also seen how these tests are to be done. It is important to choose the right equipment for performing these tests. So, let us see an example how we will choose the meters and other equipment for performing these tests.
(Refer Slide Time: 35:38)

Let us say we have a 200 volt by 400 volt single phase transformer and rated at 4 KVA. I want to perform no load and short circuit test on this transformer. So, what should be the rating of different equipments that I should choose? Now for this transformer the rated voltages are for the LV side 200 volts, for the HV side 400 volts; related currents for the LV side it is 4 KVA by rated voltage equal to 20 amperes. On the HV side the rated voltage is 4 KVA divided by rated voltage equal to 10 amperes. So, for the LV side ratings are 200 volt 20 amperes; for the HV side rated voltages are 400 volts 10 amperes.
(Refer Slide Time: 38:10)
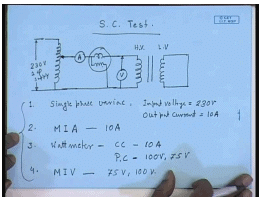
Let us just look at first the short circuit test; this is done on the HV side. So, it will be done on the 400 volt side with the 200 volt side shorted. The measurements required are we have to measure the voltage; you will have to measure the power, and you will have to measure the current. Normally when the transformer is shorted it requires very little current to very little voltage to circulate the full load current; therefore, this is supplied from a single phase variac. So, the equipment required are, this is the rated 220 volt or 230 volt single phase supply. Equipment required first is single phase variac; its input voltage is 230 volts. The output it should be able to carry at least the rated full load current of the single phase transformer. So, its output current should be at least 10 ampere.
Then we need an ammeter which should be able to measure ac. So, this is moving iron type ammeter. This should be able to measure 10 amperes of current. Next I need a wattmeter whose current coil should be able to carry at least 10 amperes; what about the voltage coil potential coil? Now for a single phase transformer if we look at the equivalent circuit single phase transformer. When we short the secondary side the required voltage to circulate full load current is the series impedance multiplied by the full load current which under usually is in the range of 5 to 10 percent of the rated voltage.
Therefore, for the high voltage side the rated voltage is 400 volts and at best 10 percent of it which would be required. So, the applied required voltage in no case would be possibly exceeds 50 ampere. So, let us choose a wattmeter whose potential coil can read at, say, 100 volts; it may be even lower; it can be even 50 volts possibly, but it is difficult to get wattmeter of that rating. So, it has to use 100 volt. A 75 volt is a normal rating that is usually available. So, it may be even 75 volts. Then we need a voltmeter moving iron voltmeter. Since the potential coil of the wattmeter and the voltmeter are connected to the same points the drop across the current coil being negligible; this can also be either 75 volt or 100 volt reading. So, these are the list of equipments required for the short circuit test. Now let us look at the open circuit test.
(Refer Slide Time: 43:54)
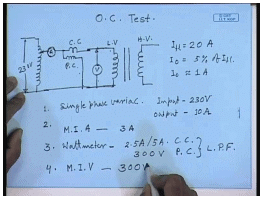
The open circuit test is done one the LV side with the HV side open circuited. Here again we need to measure the applied voltage, power and the current. Now open circuit tests are done at rated voltage. Since open circuit tests are done at rated voltage it could have been directly connected to the source, but the voltage rating of the LV side may not exactly match with the voltage available; therefore, here also normally a variac will be used.
For example, the available single phase supply may be of 230 volt, whereas, our transformer rated voltage is just 200 volt. So, we need a variac. So, now let us see what is needed. One is single phase variac; its input voltage will be 230 volts means all variac will give you up a voltage at least up to input voltage. So, this voltage rating is sufficient. The current drawn from this variac will be the no load current of the transformer which is very small; on the LV side the rated current itself is 20 ampere, the no load current of a transformer will be around 5 percent of that. So, the no load current will be within 1 ampere. So, the variac that can give 1 ampere output current should be sufficient for this test.
However, if we do both the single phase the open circuit and the short circuit test I can use the same variac that was used in case of short circuit test for doing this test. Now there the output current was specified as 10 ampere which is sufficient for to be used for the no load test. So, here also we use the same variac with an input of 230 volt and output current of 10 ampere. It should be emphasized that this 10 ampere output current is not required for this no load test. However, in order to reduce the duplication of the equipment we are using the same variac that we used for the short circuit test. Hence this is sufficient; however, if the short circuit test is not required, only open circuit test is required then we can choose a variac of much lower current rating.
Second is the ammeter; again here also we will need an ammeter moving iron ammeter. As we have already mentioned the current drawn will be simply the no load current of the transformer; for this particular case on the LV side the rated current is 20 amperes, no load current I 0 is usually within 5 percent of I f l. So, I 0 may be 1 ampere. So, again whichever ammeter we have chosen for short circuit test could have been sufficient. However, this current rating 10 ampere is too large for performing the open circuit test. The problem is the higher the maximum range of the meter the lower its accuracy, becomes particularly with moving iron equipment at the lower end the accuracy suffers. Therefore, it will be necessary to choose a lower rated ammeter.
So, let us choose something like 3 ampere rated ammeter for this test. Since, the same 10 ampere ammeter will possibly give erroneous result. Sometimes meters with multiple ranges are available. For example, we can get an ammeter of 2.5 amperes, 5 amperes and 10 amperes in which case the 2.5 ampere range can be used, same ampere can be used for both of the tests which during open circuit test we use the 2.5 ampere range; for the short circuit test we use the 10 ampere range. Similarly, for here also we will need a wattmeter, there also we will need a wattmeter. The wattmeter in this case we will have a current coil rating which is same as the ammeter current coil rating. So, preferably 2.5 ampere, 3 ampere current coil rating would have been good.
Obviously, this same wattmeter current coil will not be useful here, because here again we will have the same problem of accuracy; we cannot use a wattmeter with 10 ampere rated current. We will have to use a much lower, 2.5 ampere would be ideal; however, it is difficult to get a wattmeter. So, let us choose either a 2.5 ampere if available or a 5 ampere rating for the current coil. For the potential coil though here the applied voltage is same as the rated voltage of the LV side which is 200 volt in this case. So, we will have to choose a wattmeter whose potential coil is rated at least at 200 volts it should be more. So, we choose a wattmeter with a potential coil rating of let us, say, 300 hundred volts.
Most importantly for getting accurate result we will have to be careful about the type of the wattmeter; at no load the power factor is very poor. It is close to 0l it is less than 0.2. So, this must be a low power factor wattmeter. In the short circuit test also the power factor may be poor, but usually it is not so poor as in the case of open circuit test. So, possibly a normal wattmeter will be sufficient for short circuit test, but for no load test a special low power factor wattmeter which measures accurately below a power factor of 0.2 must be used. Finally, we will need an ac voltmeter which is a moving iron voltmeter, and since they are connected the same points as the potential coil of the wattmeter this should also be rated at 300 volts.
(Refer Slide Time: 53:37)

So, to summarize to this test the following equipments will be required. One is a single phase variac 230 volt 10 ampere MIA 0 2.5 5 10 ampere if it is available then 1; otherwise, you will have to get one 0 to 10 ampere 1 and 0 to 2.5 ampere 1. Voltmeter you can get again choose a 0 100 0 75 150 300 volts. This is a normally available voltmeter. You will need two types of wattmeter. One is LPF current coil rating 0 to 2.5 amperes, potential coil rating 300 volts. Another normal wattmeter the current coil rating 0 to 10 amperes, potential coil rating 75 volts. These are the list of equipments that would be necessary for performing the short circuit and the open circuit test on this particular transformer.





















