Characteristics of Compound DC Series Motors
In one of our previous lectures we have seen how dc shunt generators can be connected in parallel to supply a common load. A similar arrangement is sometimes possible with motors also particularly with series motors.
(Refer Slide Time: 00:35)
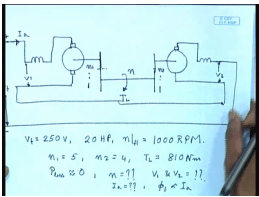
It is possible to connect mechanically coupled 2 series motors to drive a common shaft usually through a gear reduction. You can drive the same shaft whereas, the load torque is applied on the common shaft, this is N 1 is to 1 and this is N 2 is to 1, normally for series motor it is 2 machine are also electrically connected in series and connected across a supply voltage V t it is possible to adjust the loading of the motor by properly selecting the gear ratio.
Let us try to see how this is done through an example. Let us consider 2 identical dc series motors for which this V t equal to 250 volts both of them are rated at twenty hertz power and N full load that is full load equal to 1000 rpm. The gear ratio are N 1 equal to 5 and N 2 equal to 4 the total load torque t l equal to 810 newton meter if the losses are neglected p loss in both the motors are almost negligible. So, we have to find out what is the speed of this common shaft N what will be the voltage across individual motors V 1 and V 2 and what will be the common armature current I a in such an arrangement. we will also assume that phi f is proportional to I a that is the machines are unsaturated .
(Refer Slide Time: 04:11)

Now, for this particular case N 1 by N equal to 5 and N 2 by N equal to 4, therefore N 1 by N 2 equal to 5 by 4. Since, I a 1 equal to I a 2 equal to I a and phi f is proportional to I a, we have phi f 1 equal to phi f 2 equal to phi f, therefore E 1 by E 2 the induced voltages equal to phi f 1 N 1 divided by phi f 2 N 2 where these are same as phi f. So, this is equal to N 1 by N 2 equal to 5 by 4, but since r a plus r E plus r s E is approximately 0 then E 1 plus E 2 equal to V t equal to 250 volts. therefore, E 2 into 1 plus E 1 by E 2 equal to 250 volts, but we already have E 1 by E 2 equal to 5 by 4 this gives you the value of E 2 equal to 111 volts and E 1 equal to 139 volts. The voltage it is V 2 equal to V 1 equal to E 1 because the resistance drop is negligible.
(Refer Slide Time: 06:29)

Now, let us look at the torque generated T e 1 is equal to K phi f 1 I a 1 and T e 2 is equal to K 2 phi f 2 I a 2, but these are identical machines. So, K 1 equal to K 2 also phi f is proportional to I a and I a 1 equal to I a 2, and since phi f 1 equal to phi f 2 therefore, T e 1 equal to T e 2. So, both the machines they share the torque equally. Now, let us look at the mechanical arrangement [nosie] the gear ratio is N is to n. So, 5 is to 1, so if the generated torque by the motor is T e 1 then the shaft torque contribution by motor 1 is 5 times T e 1 plus 4 times T e 2, which is equal to 9 times T e this is the total shaft torque which is given as 810 Newton meter. So, T e 1 equal to T e 2 equal to T e this comes to 90 Newton meter.
Now, what about the rated torque of the machines T e rated can be found out from the rating of the machines, which are given as 20 hertz power. So, many watts divided by their rated speed 1000 rpm by 60 is the rated rps into 2 pi the rated omega this comes to 142.47 Newton meter what about I a rated again losses are negligible. So, this is the output power of the motors by the input voltage this comes to 59.68amperes. Now, we know in unsaturated dc machine T e is proportional to I a square, therefore I a in this case will be square root 90 divided by 142.47 into rated current this comes to 47.43 amperes.
(Refer Slide Time: 09:21)

Now, coming to the shaft speed the in since losses are negligible. E 1 plus E 2 into I a this should be equal to T l omega l. So, omega l equal to E 1 250 into 47.43 p by 810 and N l equal to 60 into 2 pi this comes to approximately equal to 140 rpm.
(Refer Slide Time: 11:03)
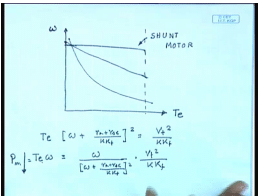
So far, we have seen 2 types of dc series motor 1is the shunt motor whose torque speed characteristics is a straight line with a little, this is the shunt motor. And, the series motor in which case the power drops very fast as the speed increases. In fact, for the series motor we know T e into omega plus r a plus r s E divided by K K f whole square equal to V t square by K K f therefore, T e omega equal to omega by plus r a plus r s E by K K f whole square into V t square by K K f. So, as the speed increases in the power output this drops in on the other hand for the shunt motor as the torque increases power output also increases, it may be desirable to get a characteristic which is somewhat in between the 2. The 1 disadvantage of dc series motor is that it is no load, it does not have a finite no load speed as the load reduces the load torque reduces thus speed can become dangerously high, which is a undesirable feature, but 1 desirable feature of this is that the as the load on the motor is increased its speed drastically falls thereby sharing a lot of power, a limiting is more or less power limited. So, in order to combine these 2 features that is in order have a definite no load speed, but a more grouping characteristics than the shunt motor I can use a compound dc motor by adding a shunt field to a series machine.
(Refer Slide Time: 14:05)
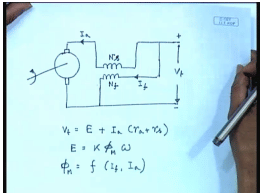
As shown below normally a long shunt cumulative connection is used that is this is a series motor to which a shunt field is also added, of course I can also see it as a shunt motor to which a series field has been added, but this can give interesting torque speed and all other characteristics. So, let us say this is the armature current I a or this machine we would write V t equal to the back emf E plus I a into r a plus r s, where E equal to K phi omega normally this phi M will be some non-linear function of the shunt field current and the series field current, but if we assume the motor magnetic circuit to be unsaturated.
(Refer Slide Time: 16:11)

We can write this phi M to be some K f into I f plus the equivalent field amperes of the armature current which is N s I a by N f N s I a is the ampere turns due to the series field and a equivalent field current is that divided by equivalent field ampere turns is that divided by N f. If we replace this then we get E equal to some K K f into I f plus N s by N f I a into omega. In other words we can write omega equal to E divided by, where E itself is V t minus r a plus r s into I a divided by K K f I f plus N s by N f I a from where we can find out the current speed characteristics of the machine as follows, so this can be written as omega into I f plus N s by N f I a equal to V t by K K f minus r a plus r s by K K f I a.
(Refer Slide Time: 19:18)

In other words omega I f plus N s by N f omega I a equal to V t by K K f minus r a plus r s divided by K K f I a we can write omega I a plus N f I f by N s omega plus N f by N s into r a plus r s divided by K K f I a equal to N f by N s into V t divided by K K f this can further be written as omega plus N f by N s into r a plus r s divided by K K f into I a plus N f I f by N s equal to N f by N s V t by K K f plus N f by N s whole square r a plus r s divided by K K f I f is equal to N f by N s into 1 by K K f into V t plus r a plus r s N f I f by N s. So, this is the current speed characteristics of the compound cumulatively compound long shunt d c series motor please note that on the right hand side for constant terminal voltage and constant values of I f the right hand side is constant. So, this is again the equation of a rectangular hyperbola, but not with omega or I axis as the asymptotes, now the asymptotes are slightly different.
(Refer Slide Time: 23:19)
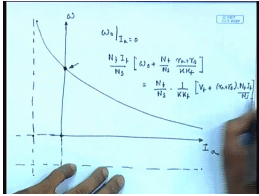
So, this is omega this is I a these asymptotes are somewhat different the interesting point to note is that at no load that is at armature current equivalent to 0 the omega does not become infinity here. In fact, we can find out what will be this no load speed that is omega 0 at I a equal to 0 from the given torque speed equation by setting I a equal to 0. In this equation we get N f I f by N s into omega 0 plus N f by N s r a plus r s divided by K K f this should be equal to N f by N s into 1 by K K f V t plus r a plus r s into N f I f by N s or in other words we can write omega 0 plus.
(Refer Slide Time: 26:01)

N f by N s into r a plus r s divided by K K f equal to V t by K K f I f plus r a plus r s N f I f divided by N s into K K f I f this comes to V t by K K f I f plus N f by N s into r a plus r s divided by K K f or omega 0 comes to V t divided by K K f I f equal to V t divided by K phi just as the shunt motor with just the shunt motor field winding this is excepted. Now, let us look at the torque speed characteristics or torque current characteristics first for this machine. The torque of this machine is given by just as any other dc machine it would be K phi M I a, but phi M itself equal to K f into I f plus N s I a by N f, therefore T e equal to K K f into I f plus N s I a by N f into I a.
(Refer Slide Time: 29:20)

In other words, this can be written as K K f N s by N f into I a plus N f I f by N s into I a, but we have seen that, so this is equal to K K f N s by N f into I a square plus N f I f by N s I a. This can be written as N f I f by 2 N s whole square minus N f I f by 2 N s whole square equal to K K f N s by N f into I a plus N f I f by 2 N s whole square minus K K f N s by N f into N f square.
(Refer Slide Time: 32:50)
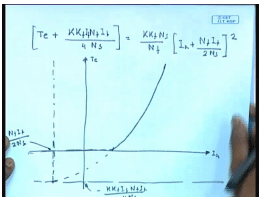
I f square by 4 N s square or T e plus K K f N f I f square divided by 4 N s equal to K K f N s by N f into whole square or so this is also a equation of a parabola, but not with the normal axis of T e and I a rather here also the torque current characteristics is followed given by this equation. I am sorry T e plus K K f N f, you can write this as K f I f N f I f divided by 4 N s. This is equal to K K f N s by N f I a plus N f I f by 2 N s whole square. So, this gives you a torque speed characteristics somewhat like this point is minus K K f I f N f I f by 4 N s, and this point is N f I f by 2 N s looks somewhat like this. We can also find out the torque speed characteristics by simply substituting the value of current.
(Refer Slide Time: 38:19)

We have seen T e to be equal to K K f I f plus N s I a by N f into I a, and we have also seen from the current speed characteristics omega plus N f by N s r a plus r s divided by K K f into I a plus N f I f by N s equal to N f by N s K K f into V t plus r a plus r s N f I f by N s from this we can write T e equal to K K f N s by N f I a plus N f I f by N s into I a from here, we can find out I a plus N f I f by N s to be equal to N f divided by N s K K f into V t plus r a plus r s N f I f by N s divided by omega plus N f by N s r a plus r s by K K f. Now, this value of I a plus N f I f by N s can be substituted in the torque equation as well as the value of I to get the torque speed characteristics.
(Refer Slide Time: 41:13)
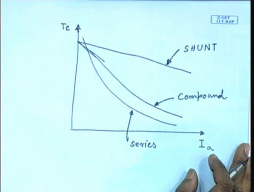
And the torque speed characteristics for this machine comes somewhat like this looks somewhat in between the dc shunt and the dc series motor whereas, for this series motor the torque speed characteristics would have been somewhat like this and for the shunt motor, it would have been this is shunt, this is series and this is compound similarly we can find out the other characteristics for example, the speed current characteristics rpm.
(Refer Slide Time: 42:25)
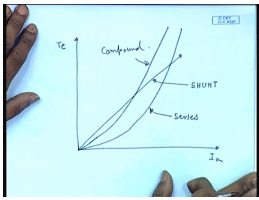
Whereas for the shunt it is again straight line and for the series, this is rectangular hyperbola for compound it is also a rectangular hyperbola, but not with these 2 as asymptotes. So, this looks somewhat like this, so this is shunt this is series, and this is compound it should be understood that we are talking about cumulatively compound motors the torque speed characteristics for shunt. We know it is a straight line for series this is the series for cumulatively compound. We will get something in between this will be shunt this is series this is compound the interesting thing is these characteristics of shunt and series machines. The compound machine can be controlled by controlling the proportion of the series or shunt field ampere turns as a percentage of the total ampere turns of the machine.
(Refer Slide Time: 45:04)

Let us look at it through an example let us consider a cumulatively compound dc motor the characteristics is its starting torque equal to 150 percent of the full load torque while the starting current is 130 percent of the full load current the full load armature drop is 12 percent of the rated voltage whereas, no load armature drop is just 2 percent of the rated voltage for this we have to find out what is the shunt ampere turns as percentage of net ampere turns at full load, we have to find out what is the percentage of shunt ampere turns as the percentage of the total ampere turns at full load and also what is the no load as percentage of full load for these characteristics, we have to find out how much shunt ampere turns will be necessary and what no load speed would it give as percentage of the full load speed.
(Refer Slide Time: 47:41)

To solve this problem, we note that T start equal to K K f into I f plus N s by N f I a start into I a start this can be written as K K f I a start into N f I f plus N s I a start divided by N f similarly full load equal to K K f I f I a full load into N f I f plus N s I a full load divided by N f I f now if we divide then T starting by T full load which is 1 point four this comes to N f I f plus N s I a at starting divided by N f I f plus N s I a at full load this is equal to 1 plus N s I a at starting minus I a at full load divided by N f I f plus N s I a at full load this into I a start divided by I a full load into I a start divided by I a full load. Now, this again is 1.3.
(Refer Slide Time: 50:41)

Therefore, we have 1.4 divided by 1.3 equal to 1 plus N s I a start minus I a full load divided by N f I f plus N s I a full load equal to 1 plus N s I a full load into I a start by I a full load minus 1 divided by N f I f plus N s I a f l. Therefore, 14 by 13 minus 1 equal to N s I f l I a f l divided by N f I f plus N s I a f l into this thing is known as 1.3 minus 1. Therefore N s I a f l divided by N f I f plus N s I a f l equal to 1 by 13 into 1 by .3 equal to 10 by 39, therefore the field ampere turns N f I f divided by N f I f plus N s I a f l as a percentage of net ampere turns equal to 1 minus 10 divided by 39 comes to 29 by 39 which is 74 percent.
(Refer Slide Time: 53:23)

And, to find out no load speed we note that I a r a plus r s E at full load equal to 0.12 p u I a r a plus r s E at no load equal to 0.02 p u. So, E at full load equal to 0.88 p u E at no load equal to 0.98 p u phi at no load divided by phi at full load equal to N f I f plus N s I a no load divided by I f plus N a I a full load this is equal to 0.74 plus N a I a full load divided by N a I f plus N a I a full load into I a no load divided by I a full load this comes to .7833.
(Refer Slide Time: 55:06)

And, E no load divided by E f l equal to phi no load into N no load divided by phi full load into N full load therefore, N no load divided by N full load equal to phi full load divided by phi no load into E no load divided by E full load. This comes to 1 by 0.7833 into 0.98 divided by 0.88 this is 142 percent.
Thank you.


























