Variational Principle : Euler-Lagrange Equation and its Applications - 2 | Physics for IIT JAM, UGC - NET, CSIR NET PDF Download
Example: Planetary Motion
Consider the motion of a planet due to the force exerted by Sun. Using polar coordinates we can write the Lagrangian for the planet as
We have
The Euler- Lagrange equation for the angle variable is
which gives
(8)
This is the statement of conservation of energy which follows from Kepler's second law.
The equation for the radial variable is
from which we get
Substituting from (8), we can write this as
From the above we get
(9)
which is a statement of conservation of energy.
Validity of Euler Lagrange Equation in Generalized Coordinates
t was seen that the degrees of freedom of two particles connected by a rigid rod is 5, and not 6, as the constraint of keeping the length xed bewteen the two masses reduces the number of independent quantities by 1. It is easy to see that a rigid body has 6 degrees of freedom, independent of the number of particles N . This is seen by the following argument. Starting with two particles, which has ve degrees of freedom, add a third particle non-collinear with the former two. This should increase the degree of freedom by 3. However, we have now introduced two additional constraints, viz., the distance between this newly added particle and the former two must remain constant. These two constraints, therefore, add only one additional degree of freedom and not three. Thus a system of rigidly connected three non-collinear masses brings in only one additional degree of freedom, making the number of degrees of freedom 6. If we now add a 4th particle, we bring in three constraints requiring that the distance between the 4th particle and the earlier three. Thus the 4th particle does not bring in any more degrees of freedom. The argument can now be repeated when we add more particles as the only independent constraints are three, distance between keeping the distance between the newly added particle and any three non-collinear particles being given, determines all other distance uniquely. Thus a rigid body can only have 6 degrees of freedom.
If the number of degrees of freedom is 3N - k = d, k being the number of independent constraints, the number of generalized coordinates required to specify the con guration of the system is d. We could, of course, choose any d cartesian coordinates x1, x2,........., xd for this purpose. However, this choice is not unique. Let qj be d functions ofthese x1, x2,........., xd with a non-vanishing Jacobian,
The new qis need not even have the dimension of length (e.g. in spherical polar, the coordinates θ and φ are dimensionless.) This new set q1, q2,..........,qd are known as the generalized coordinates.
Since are independentt of one another, the velocities
are also independent set. These are known as the generalized velocities. [Lest there is confusion, I wish to emphasize that the number of generalized coordinates for a system with 3N degrees of freedom is 3N , it is only when the constraints are taken care of, it reduces to 3N k and one only needs these many independent coordinates to completely specify the system.]
We denote by the partial derivative of xi with respect to qj , when the remaining d 1 generalized coordinates are held xed.The real velocities associated with xi = dxi/dt and
If xi has no explicit time dependence (time dependence could arise, for instance, due to moving constraints), the last term of the above vanishes and we are left with
which gives
This relationship is referred as Dot Cancellation Theorem.
We will now show that the validity of the Euler Lagrange equation is not restricted to the Cartesian coordinates alone; they are equally valid in generalized coordinates. We have
(10)
We also have,
(11)
where, in the last step, we have used in dot-cancellation relation. Taking time derivative of both sides of (11), we get
(12)
since the last term is zero because the velocities are independent of the generalized coordinates. This establishes Euler Lagrange equation for the generalized coordinates.
The Brachistoschrone Problem
The word "Brachistochrone" is derived from the greek words brachistos meaning the shortest and chromous meaning time - i.e. it is about the shortest time problem.
Consider a bead sliding frictionlessly along a wire in a vertical plane from the point (x1, y1) to the point (x2, y2), where y2 lies lower than than y1. The problem is to design a path for which the time to slide is the shortest. Let us take the origin to be at the rst point (x1, y1) and take y to be positive downwards. The shape of the wire is given by y = f (x) ≥ 0. The wire is taken to lie below and to the right of the origin so that x ≥ 0 and y ≥ 0 along its path.
The time to come down is
The speed of the bead as it comes down is determined by the conservation of energy. Since y is positive downwards, the total energy must remain zero if the potential energy is taken to be zero at the origin. Thus we must have
Thus
It is convenient to convert this to an integral over y
where x' = dx/dy. Thus the Lagrangian function is a function of x' and y.
Euler-Lagrange equation is
As has no dependence on x, the rst term of the above vanishes
is constant.
so that
where we have, for reasons to become clear later, chosen the constant to be 1=2R.
This gives
resulting in
We can parameterise the above by taking
Thus the shortest path is given by the pair of parameterised equations
These are parametric equations for a cycloid.
Fig. 5: The path of a brachistochrone is shown in red
The lowest point of the brachistochrone corresponds to θ = π. The path is a curve traced out by a xed point on the circumference of a circle of radius R as the circular disk moves on a horizontal
oor. The constant R is determined by the condition that the curve must pass through the point y = y2. Thus if y2 is the lowest point then y2 y1 = 2R. an interesting point is that the time taken to descend to the lowest point is independent of the point from which it was released, i.e., it speeds up appropriately to cover the distance to the lowest position in the same time. The time is calculated as follows:
With the above substitution, i.e.,
we have,
(15)
The Spring Pendulum
As a second example, we consider a spring pendulum, in which the bob of the pendulum is connected to the support not by means of an inextensible string but by means of a spring whose length can only vary along its length (this can be achieved by encasing the spring in tube, for instance).
Let the instantaneous distance of the bob from the support be l + x, where l is the natural length of the spring. We choose x to be one of the generalized coordinates and the angle θ that the spring makes with the vertical as the other (note that unlike the case of simple pendulum which only had one degree of freedom, we now have two). The kinetic
and the potential energies of the system are given in terms of these coordinates and the corresponding velocities as
The Lagrangian is of course, L = T − V . The Euler- Lagrange equations for the x coordinates are
The equation is readily identifiable as the equation for the radial acceleration with the first term on the right being the centripetal acceleration term 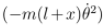 which should be taken to the left to give the total radial acceleration. The second term is the radial component of the weight and the third term is the spring force. The equation (16) can be interpreted in the rotating frame in which case the first term gives the centrifugal force. The equation for the θ coordinate is
which should be taken to the left to give the total radial acceleration. The second term is the radial component of the weight and the third term is the spring force. The equation (16) can be interpreted in the rotating frame in which case the first term gives the centrifugal force. The equation for the θ coordinate is
(17)
The right hand side of this equation is the torque of the weight about the point of suspension. The left hand side is the rate of change of the angular momentum as can be easily seen, since the tangential velocity is and the distance from the support is (l + x). Explicitly differentiating (17) and cancelling a common factor, we can rewrite this equation as
This can be interpreted in the rotating frame, the rst term being the angular acceleration term and the second the Coriolis term.
FAQs on Variational Principle : Euler-Lagrange Equation and its Applications - 2 - Physics for IIT JAM, UGC - NET, CSIR NET
| 1. What is the Euler-Lagrange equation? |  |
| 2. How is the Euler-Lagrange equation derived? |  |
| 3. What are the applications of the Euler-Lagrange equation? |  |
| 4. Can the Euler-Lagrange equation be used to solve real-world problems? |  |
| 5. Are there any limitations or assumptions associated with the Euler-Lagrange equation? |  |
















