Number System Class 9 Notes Maths Chapter 1
| Table of contents |

|
| Introduction |

|
| 1. Natural Numbers |

|
| 2. Whole Numbers |

|
| 3. Integers |

|
| 4. Rational Numbers |

|
| Rational Numbers Between Two Given Rational Numbers: |

|
| 5. Irrational Numbers |

|
| 6. Real Numbers |

|
Introduction
- The numbers of the form p/q, where ‘p’ and ‘q’ are integers and q ≠ 0, are called rational numbers.
- A rational number p/q is said to be in the simplest form if ‘p’ and ‘q’ (q ≠ 0) are integers having no common factor other than 1.
- Every rational number can be expressed as a decimal. If the decimal expression of p/q terminates, then it is called a terminating decimal.

- A rational number p/q (in simplest form) is a terminating decimal only when prime factors of ‘q’ are 2 or 5 or both.
- A decimal in which a digit or a group of digits repeats periodically is called a recurring decimal.
- The decimal expression of a rational number is either terminating or non-terminating recurring.
- An irrational number is a number that cannot be expressed as the ratio of two integers.
- The decimal expression of an irrational number is non-terminating and non-recurring.
- If ‘r’ is rational and ‘s’ is irrational, then for r ≠ 0, all r + s, r – s, r * s and r/s are irrational.
- The collection of all rational and irrational numbers is called real numbers.
- The process of converting the irrational denominator of a number by multiplying its numerator and denominator by a suitable number is called rationalization.
 Types of Numbers
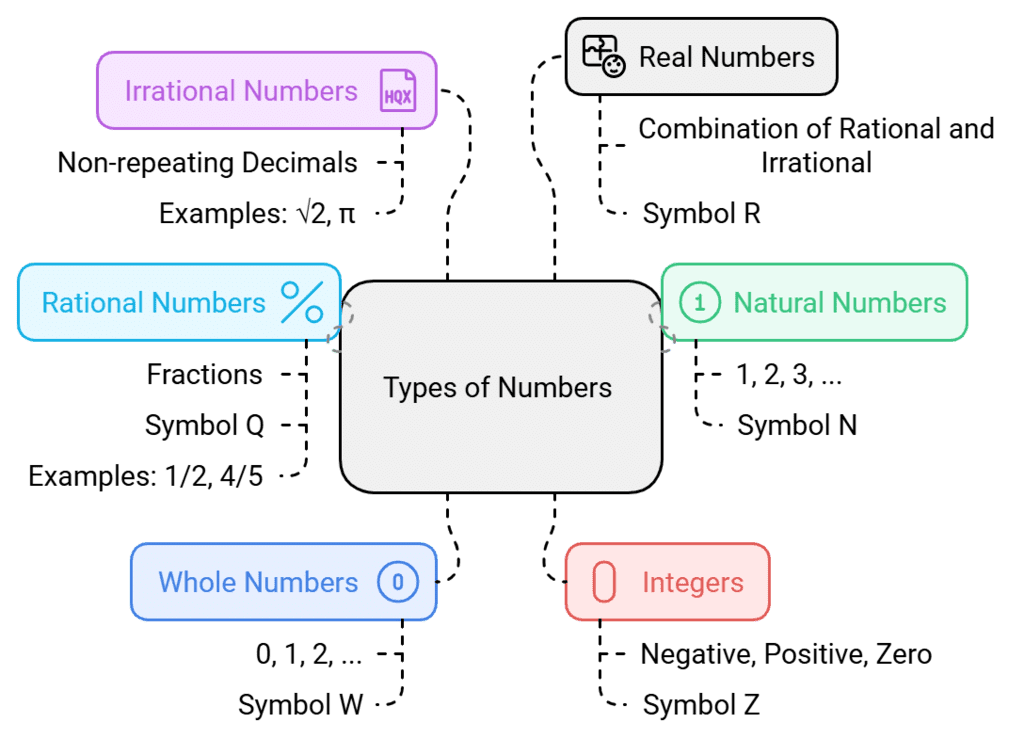
Types of Numbers
1. Natural Numbers
- Counting numbers like 1, 2, 3, 4, … are called natural numbers.
- We denote the collection of natural numbers by ‘N’.
2. Whole Numbers
- All natural numbers together with zero are called whole numbers.
- We denote the group of whole numbers by the symbol ‘W’.
3. Integers
- The negative numbers, the positive numbers, and zero together form the set of integers.
- The set (collection) of all integers is denoted by the symbol ‘Z’.
Note: The symbol Z is taken from the German word “Zählen”, which means “to count”.
4. Rational Numbers
- A number that can be represented in the form of p/q is called a rational number.
- Rational numbers include natural numbers, integers, and all the (negative and positive) fractions.
- The collection of rational numbers is denoted by the symbol ‘Q’.
Example: 1/2, 4/5, 26/8, etc.
Note: The symbol Q comes from the word ‘quotient’ and the word ‘rational’ comes from ‘ratio’.
Rational Numbers Between Two Given Rational Numbers:
- There are an infinite number of rational numbers between any two given rational numbers.
- Important Results
(i) Let ‘x’ and ‘y’ be two rational numbers.
A rational number lying between ‘x’ and ‘y’ = (x + y)/2.
(ii) Let ‘x’ and ‘y’ be two rational numbers such that x < y.
To find ‘n’ rational numbers between ‘x’ and ‘y’, letThen ‘n’ rational numbers between ‘x’ and ‘y’ are: (x + d); (x + 2d), (x + 3d), … (x + nd)
This is known as the method of finding rational numbers in one step.
5. Irrational Numbers
- A number that cannot be written in the form of p/q, (where p and q are integers and q ≠ 0), is called an irrational number. We denote an irrational number by ‘S’.
- Examples: √2, √3, √5, √6, √11, π, 0.10110111011110...., etc., are not rational numbers, so they are irrational numbers.
Note:
(i) An irrational number can be written as a decimal, but not as a fraction. An irrational number has endless non-repeating digits to the right of the decimal point i.e., an irrational number is an infinite decimal.
(ii) Irrational numbers are rarely used in daily life, but they do exist on the number line. In fact, on the number line, between 0 and 1, there are an infinite number of irrational numbers.
Properties of Irrational Numbers
- These satisfy the commutative, associative and distributive laws for addition and multiplication.
- The sum of the two irrationals need not be irrational.
Example: (2 + √3) + (4 – √3) = 6 - The difference between the two irrationals need not be irrational.
Example: (5 + √2) – (3 + √2) = 2 - The product of the two irrationals need not be irrational.
Example: √3 x √3 = 3 - The quotient of the two irrationals need not be irrational.
Example: (2√3)/√3 = 2 - The sum of rational and irrational is irrational.
- The difference between a rational number and an irrational number is irrational.
- The product of a rational and an irrational number is irrational.
- The quotient of a rational and an irrational number is irrational.

Special Properties of Rational and Irrational Numbers
- Every rational number can either be a terminating decimal or a non-terminating repeating (recurring) decimal.
- Every terminating decimal is a rational number.
- Every repeating decimal is a rational number.
- An irrational number can neither be a terminating decimal nor a repeating decimal.
- The square root of any prime number is an irrational number.
If ‘m’ is a positive integer but not a perfect square, then √m is an irrational number. i.e. √1 = 1, rational number;
√2, irrational number
√3, irrational number
√4 = 2, rational number
√5, irrational number
√6, √7, √8 irrational number
√9 = 3 rational numberIf ‘m’ is a positive integer but not a perfect cube, then ∛m is an irrational number. So ∛2, ∛3, ∛4, ∛5, ∛6, ∛7,.. are irrational number
But ∛1 = 1, rational number
∛8 = 2, rational number
∛27 = 3, rational number
∛64 = 4, rational number
 |
Download the notes
Short Notes: Number System
|
Download as PDF |
6. Real Numbers
- The collection of all rational numbers and irrational numbers together makes up a collection of real numbers.
- The collection of real numbers is denoted by ‘R’.
- The square of a real number is always non-negative(≥0).
Remember
(i) Every real number is either rational or irrational.
(ii) Between any two real numbers exists an infinite number of real numbers.
(iii) On the number line, each point corresponds to a unique real number. On the other hand, every real number can be represented by a unique point on the number line. That is why we call a “number line” a “real-line” also. All numbers, positive and negative, integers and rational numbers, square-roots, cube-roots, π (pi) are present on a number line
(iv) Real numbers follow Closure property, associative law, commutative law, the existence of a multiplicative identity, the existence of multiplicative inverse, and Distributive laws of multiplication over Addition for Multiplication.
Real Numbers and Their Decimal Expansions
(a) The Decimal Representation of Rational Numbers
- All rational numbers can be expressed as decimal numbers.
- A rational number in the form of p/q, (q ≠ 0), on the division of ‘p’ by ‘q’, either the remainder becomes zero or never becomes zero.
Examples:
Remainder = 0
Quotient = 0.375
Here, the decimal expansion ends (terminates) after a finite number of steps, such numbers are called terminating.
Remainder: Every time we get the remainder 2, it will never end.
Quotient: 0.666…, i.e. the digit 6 is repeating every time.
Here, the decimal expansion does not end (does not terminate) even after an infinite number of steps. Such numbers are called non-terminating.
(iii)
Remainder: We are getting the remainder as 3 and 8 alternatively.
Quotient: The digits after the decimal point are repeated in a block of two digits, i.e. ‘2’ and ‘7’.
In such cases, the decimal expansion goes on forever, and we get a repeating block of digits in the quotient. We call such numbers non-terminating repeating (or non-terminating recurring).
Remember
(i) The number of digits in the repeating block is always less than the divisor.
(ii) The decimal expansion of a rational number is either terminating or non-terminating recurring (repeating).
(b) The Decimal Representation of Irrational Numbers
- The decimal expansion of an irrational number is non-terminating and non-recurring (non-repeating).
- Example:
(i) 0.10110111011110....
(ii) √3 = 1.732050807...
(iii) √7 = 2.645751311 ...
(iv) π = 3.14159265358 ....
(v) √2 = 1.41421356237 ....
Note: Generally we take π = 22/7 which is not true. In fact π is an irrational number having a value which is non-terminating and non-repeating, i.e. π = 3.1415926535897932384… whereas 22/7 is rational number whose value is non-terminating repeating, i.e. 22/7 = 3.142857142857…
Thus, π and 22/7 are same only up to two places of decimal.
Rationalization
- When a number is such that its denominator is irrational, then we need it to be rationalized.
- The process of converting an irrational denominator of a number to a rational number by multiplying its numerator and denominator by a suitable number is called rationalization.
Rationalizing Factor (RF)
If the product of two rational numbers is rational, then each one is called the rationalizing factor of the other.
(i) If ‘a’ and ‘b’ are integers, then
(a + √b) and (a - √b) are RF of each other.
(ii) If ‘x’ and ‘y’ are natural numbers, then
(√x+ √y) and (√x - √y) are RF of each other.
(iii) If ‘a’ and ‘b’ are integers and ‘x’ and ‘y’ are natural numbers, then
(a +b√x) and (a -b√x) are RF of each other.
Laws of Exponents
If a > 0 and b > 0 are real numbers, ‘m’ and ‘n’ are rational numbers, then we have
- am x an = am+n
- am ÷ an = am-n
- (am)n = amn
- am x bm= (ab)m
- am/bm = (a/b)m
- a0 = 1
- a-n = 1/an
Representing Real Numbers on the Number Line (Old Syllabus)
- We know that there is a unique real number corresponding to every point on the number line. Also, corresponding to each real number, there is a unique point on the number line.
- The process of successive magnification helps us to locate a real number on the number line.
Note: The process of visualization of representing a decimal expansion on the number line is known as the process of successive magnification.
|
40 videos|419 docs|51 tests
|
FAQs on Number System Class 9 Notes Maths Chapter 1
| 1. What are natural numbers and how do they differ from whole numbers? |  |
| 2. Can you explain what integers are and give some examples? |  |
| 3. What are rational numbers, and how can we find rational numbers between two given rational numbers? |  |
| 4. What are irrational numbers, and can you give examples of common ones? |  |
| 5. How do real numbers encompass both rational and irrational numbers? |  |