Class 10 Maths Chapter 1 Question Answers - Real Numbers
Q1: Given that HCF (150, 100) = 50. Find LCM (150, 100).
Sol: LCM × HCF = Product of the two numbers
∴ 150 × 100 = LCM × HCF
⇒ LCM × 50 = 150 × 100
⇒ 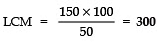
Q2: Given that LCM (26, 91) = 182. Find their HCF.
Sol: ∵ HCF × LCM = Product of the two numbers
∴ HCF × 182 = 26 × 91
⇒ 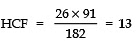
Q3: The LCM and HCF of the two numbers are 240 and 12 respectively. If one of the numbers is 60, then find the other number.
Sol: Let the required number be ‘x’.
∵ LCM × HCF = Product of the two numbers
∴ 60 × x = 240 × 12
⇒ 
Q4: The decimal expansion of the rational number, 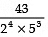 will terminate after how many places of decimal?
will terminate after how many places of decimal?
Sol:
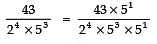
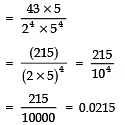
Thus, 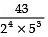 will terminate after 4 places of decimal.
will terminate after 4 places of decimal.
Q5: What is the exponent of 3 in the prime factorisation of 864.
Sol: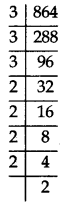
Making prime factors of 864. ,⇒ 864 = 3 × 3 × 3 × 2 × 2 × 2 × 2 × 2= 33 × 25
∴ Exponent of 3 in prime factorisation of 864 = 3.
Q6: State the fundamental theorem of arithmetic.
Sol: Fundamental Theorem of Arithmetic: Every composite number can be expressed as a product of prime numbers, and this factorisation is unique, except for the order of the prime factors.
- A composite number can be broken down into prime factors.
- This factorisation is unique; the same primes can be arranged in different orders.
- For example, 2 × 3 × 5 is the same as 3 × 2 × 5.
This theorem is essential in number theory and has significant implications in various mathematical fields.
Q7: Define an irrational number.
Sol: Irrational numbers are those that cannot be expressed as a fraction of two integers. They have the following characteristics:
- Their decimal expansion does not terminate or repeat.
- They cannot be written in the form p/q, where q ≠ 0.
Examples of irrational numbers include: √2, √3, π
Q8: Write the condition for a rational number which can have a terminating decimal expansion.
Sol: A rational number x = p/q can have a terminating decimal expansion if the prime factorisation of q is of the form of 2n · 5m, where m and n are non-negative integers.
Q9: Write the condition for a rational number which has a non-terminating repeating decimal expansion.
Sol: A rational number x = p/q can have a non-terminating repeating decimal expansion if:
- The prime factorisation of q is not of the form 2n x 5m,
- where n and m are non-negative integers.
Q10: Can two numbers have 24 as their HCF and 7290 as their LCM? Give reasons.
Sol: No, because HCF always divides LCM but here 24 does not divide 7290.
Q11: If 6n is a number such that n is a natural number. Check whether there is any value of n ∈ N for which 6n is divisible by 7.
Sol: ∵ 6 = 2 × 3
∴ 6n = (2 × 3)n = 2n × 3n
i.e., the prime factorisation of 6n does not contain the prime number 7 thus the number 6n is not divisible by 7.
Q12: Write 98 as the product of its prime factors.
Sol: ∵
The prime factorisation of 98 = 2 × 7 × 7
⇒ 98 = 2 × 72
Q13: Without actually performing the long division, state whether  will have a terminating or non-terminating repeating decimal expansion.
will have a terminating or non-terminating repeating decimal expansion.
Sol: Let =
∵ Prime factors of q are not of the for 2n · 5m.
- If the prime factors of q are only 2 and 5, the decimal expansion is terminating.
- If q has any prime factors other than 2 or 5, the decimal expansion is non-terminating repeating.
∴ will have a non-terminating repeating decimal expansion.
Q14: Without actually performing the long division, state whether 17/3125 will have a terminating decimal expansion or a non-terminating repeating decimal expansion.
Sol: ∵ The denominator of 17/3125 is given by
3125 = 5 × 5 × 5 × 5 × 5
= 1 × 55
= 20 × 55 |∵ 20 = 1
∴ 
Since the prime factorisation includes only the primes 2 and 5, it indicates that:
The decimal expansion of 17/3125 is a terminating decimal.
Q15: Express 156 as a product of its prime factors.
Sol: ∵ 156 = 2 × 78
= 2 × 2 × 39
= 2 × 2 × 3 × 13
∴ 156 = 22 × 3 × 13
Q16: If the product of two numbers is 20736 and their LCM is 384, find their HCF.
Sol: ∵ LCM × HCF = Product of two numbers
∴ 384 × HCF = 20736
⇒ HCF = 20736 /384 = 54.
Q17: Find the LCM and HCF of 120 and 144 by the Fundamental Theorem of Arithmetic.
Sol: We have 120 = 2 × 2 × 2 × 3 × 5 = 23 × 3 × 5
144 = 2 × 2 × 2 × 2 × 3 × 3 = 24 × 32
∴ LCM = 24 × 32 × 5 = 720
HCF = 23 × 3 = 24
Q18: Find the HCF × LCM for the numbers 100 and 190.
Solution: HCF × LCM = 1st Number × 2nd Number
= 100 × 190 = 19000.
Q19: Find the (HCF × LCM) for the numbers 105 and 120.
Solution: HCF × LCM = 1st number × 2nd number
= 105 × 120 = 12600.
Q20: Write a rational number between √2 and √3.
Sol: ∵ √2 = 1.41 ..... and
√3 = 1.73 .....
∴ one rational number between 1.41 .....and 1.73 ..... is 1.5
i.e., one rational number between √2 and √3 is 1.5.
|
127 videos|584 docs|79 tests
|
FAQs on Class 10 Maths Chapter 1 Question Answers - Real Numbers
| 1. What are real numbers? |  |
| 2. How are real numbers classified? |  |
| 3. What is the significance of the number line in real numbers? |  |
| 4. Can real numbers be negative? |  |
| 5. How do you perform basic operations with real numbers? |  |






















