Class 10 Maths Chapter 1 Important Question Answers - Real Numbers
| Table of contents |

|
| Very Short Answer Type Questions |

|
| Short Answer Type Questions- I |

|
| Short Answer Type Questions- II |

|
| Long AnsweType Questions |

|
| Case Based Type Questions |

|
Very Short Answer Type Questions
Q1: For any two integers, the product of the integers = the product of their HCF and LCM. Is this relation true for three or more integers?
Ans: No
Q2: The decimal expansion of the rational number 43/2453 will terminate after how many places of decimals?
Ans: We have
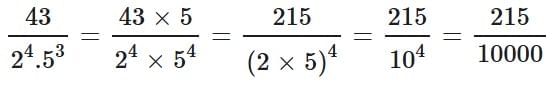 = 0.0215
= 0.0215
So, it will terminate after 4 places of decimals.
Q3: Write one rational and one irrational number lying between 0.25 and 0.32.
Ans: Given numbers are 0.25 and 0.32.
Clearly,
0.30 = 30100 = 310
Thus 0.30 is a rational number lying between 0.25 and 0.32. Also 0.280280028000.....has non-terminating non-repeating decimal expansion. It is an irrational number lying between 0.25 and 0.32
Q4: Express 98 as a product of its primes.
Ans: 98 = 2 × 7 × 7 = 2 × 7²
Q5: HCF and LCM of two numbers is 9 and 459 respectively. If one of the numbers is 27, find the other number.
Ans: We know,
1st number × 2nd number = HCF × LCM
⇒ 27 × 2nd number = 9 × 459
⇒ 2nd number = 9×45927 = 153
Q6: If HCF(336, 54) is 6 = , find LCM(336, 54).
Ans: HCF × LCM = Product of number
6×LCM = 336×54
LCM = 336 x 546
= 56 × 54 = 3024
Thus LCM of 336 and 54 is 3024.
Q7: a and b are two positive integers such that the least prime factor of a is 3 and the least prime factor of b is 5. Then calculate the least prime factor of (a+b).
Ans: Given that a is a positive integer and 3 is least prime factor of a. Also, b is a positive integer and 5 is a least prime factor of b.
Since, least prime factor of a is 3, it implies that a is an odd number.
Similarly, b is also an odd number and we know that
odd + odd = even
So, a + b = even
The least prime factor of (a + b) is 2.
Q8: Calculate the HCF of 33×5 and 32×52.
Ans: We have 33×5 = 32 × 5 × 3
32×52 = 32 × 5 × 5
HCF (33×5, 32×52) = 32 ×5
9 × 5 = 45
Q9: Calculate 3/8 in the decimal form.
Ans:
38 = 323 = 2 × 5323 × 53
= 375103 = 3751,000
= 0.375
Q10: If HCF (a, b) = 12 and a × b = 1800, then find LCM (a,b).
Ans: HCF (a, b) × LCM (a, b) = a × b
Substituting the values we have
12× LCM (a, b) = 1800
LCM (a, b) = 1,80012 = 150
Q11: Find LCM of numbers whose prime factorisation are expressible as 3 × 52 and 32 × 72.
Ans: LCM (3×52, 32×72) = 32×52×72
= 9 × 25 × 49
= 11025
Q12: Find the least number that is divisible by all numbers between 1 and 10 (both inclusive).
Ans: The required number is the LCM of 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,
LCM = 2×2×3×2×3×5×7 = 2520
Short Answer Type Questions- I
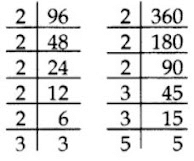
Q13: Find the LCM of 96 and 360 by using fundamental theorem of arithmetic.
Ans: 96 = 25 × 3
360 = 23 × 32 × 5
LCM = 25 × 32 × 5 = 32 × 9 × 5 = 1440
Q14: Find the largest number which divides 70 and 125 leaving remainder 5 and 8 respectively.
Ans: It is given that on dividing 70 by the required number, there is a remainder 5.
This means that 70 – 5 = 65 is exactly divisible by the required number.
Similarly,
125 – 8 = 117 is also exactly divisible by the required number.
65 = 5 × 13
117 = 32 × 13
HCF = 13
Required number = 13
Q15: Find HCF and LCM of 404 and 96 and verify that HCF × LCM = Product of the two given numbers.
Ans: 404 = 2×2×101
= 22 ×101
96 = 2×2×2×2×2×3
= 25×3
HCF (404, 96) = 22 = 4
LCM (404, 96) = 101×25×3 = 9696
HCF × LCM = 4×9696 = 38784
Also, 404×96 = 38784
Hence, HCF × LCM = Product of 404 and 96
Q16: Given that HCF (306,1314) = 18. Find LCM of 306,1314
Ans: HCF (306,1314) = 18
LCM (306,1314) = ?
Let a = 306 and b = 1314, then we have
LCM (a,b) × HCF (a,b) = a×b
Substituting values we have,
LCM (a,b)× 18 = 306 × 1314
LCM (a, b) = 306 x 131418
LCM (306, 1314) = 22,338
Q17: Complete the following factor tree and find the composite number x.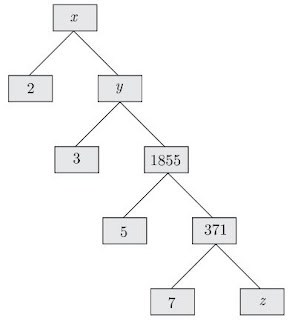
Ans: z = 371/7 = 53
y = 1855×3 = 5565
x = 2 × y = 2×5565 = 11130
Thus complete factor tree is as given below.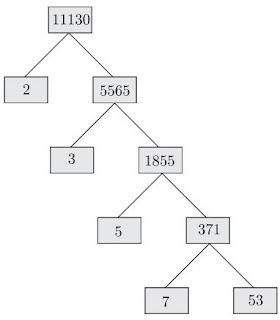
Q18: Check whether 4n can end with the digit 0 for any natural number n.
Ans: If the number 4n for any n, were to end with the digit zero, then it would be divisible by 5 and 2.
That is, the prime factorization of 4n would contain the prime 5 and 2. This is not possible because the only prime in the factorization of 4n = 22n is 2. So, the uniqueness of the Fundamental Theorem of Arithmetic guarantees that there are no other primes in the factorization of 4n. So, there is no natural number n for which 4n ends with the digit zero. Hence 4n cannot end with the digit zero.
Q19: Write the denominator of the rational number 257/500 in the form 2m × 5n, where m and n are non-negative integers. Hence write its decimal expansion without actual division.
Ans: 500 = 25 × 20
= 52 × 5 × 4
= 53 × 22
Here, denominator is 500 which can be written as 22 × 53.
Now decimal expansion,
257500 = 257 × 22 × 22 × 53 = 514103
= 0.514
Q20: Write a rational number between √2 and √3.
Ans: √2 = √200100 and √3 = √300100
We need to find a rational number x such that:
1/10√200 < x < 1/10√300
Choosing any perfect square such as 225 or 256 in between 200 and 300, we have:
x = √225100 = 1510 = 53
Similarly, if we choose 256, then we have:
x = √256100 = 1610 = 85
Q21: Can two numbers have 15 as their HCF and 175 as their LCM? Give reasons.
Ans: No,
LCM = Product of the highest power of each factor involved in the numbers.
HCF = Product of the smallest power of each common factor.
We can conclude that LCM is always a multiple of HCF, i.e., LCM = k × HCF
We are given that,
LCM = 175 and HCF = 15
175 = k × 15
⇒ 11.67 = k
But in this case, LCM ≠ k × HCF
Therefore, two numbers cannot have LCM as 175 and HCF as 15.
Q22: Explain why (17 × 5 × 11 × 3 × 2 + 2 × 11) is a composite number?
Ans: 17 × 5 × 11 × 3 × 2 + 2 × 11 …(i)
= 2 × 11 × (17 × 5 × 3 + 1)
= 2 × 11 × (255 + 1)
= 2 × 11 × 256
Number (i) is divisible by 2, 11 and 256, it has more than 2 prime factors.
Therefore (17 × 5 × 11 × 3 × 2 + 2 × 11) is a composite number.
Short Answer Type Questions- II
Q23: Prove that 3 + 2√3 is an irrational number.
Ans: Let us assume to the contrary, that 3 + 2√3 is rational.
So that we can find integers a and b (b ≠ 0).
Such that 3 + 2√3 = ab, where a and b are coprime.
Rearranging the equations, we get
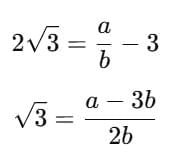
Here, 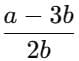 is a rational number, since a and b are integers.
is a rational number, since a and b are integers.
Thus, 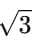 would be rational.
would be rational.
But this contradicts the known fact that 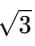 is irrational.
is irrational.
Hence, our assumption was wrong.
Therefore, 3 + 2√3 is an irrational number.
Q24: Prove that 2+√3/5 is an irrational number, given that √3 is an irrational number.
Ans: Assume that 2+√3/5 is a rational number. Therefore, we can write it in the form of p/q where p and q are co-prime integers and q ≠ 0.
2 + √35 = pq
2 + √3 = 5pq
√3 = 5p - 2q
√3 = 5p - 2qq
Since, p and q are co-prime integers, then 5p-2q/q is a rational number. But this contradicts the fact that √3 is an irrational number. So, our assumption is wrong. Therefore 2+√3/5 is an irrational number.
Q25: Write the smallest number which is divisible by both 306 and 657.
Ans: The smallest number that is divisible by two numbers is obtained by finding the LCM of these numbers
Here, the given numbers are 306 and 657.
306 = 6 × 51 = 3×2×3×17
657 = 9 × 73 = 3×3×73
LCM (306, 657) = 2×3×3×17×73 = 22338
Hence, the smallest number which is divisible by 306 and 657 is 22338.
Q26: Three bells toll at intervals of 9, 12, 15 minutes respectively. If they start tolling together, after what time will they next toll together?
Ans: 9 = 32, 12 = 22 × 3, 15 = 3 × 5
LCM = 22 × 32 × 5 = 4 × 9 × 5 = 180 minutes or 3 hours
They will next toll together after 3 hours.
Q27: Two tankers contain 850 liters and 680 liters of petrol. Find the maximum capacity of a container which can measure the petrol of each tanker in the exact number of times.
Ans: To find the maximum capacity of a container which can measure the petrol of each tanker in the exact number of times, we find the HCF of 850 and 680.
850 = 2 × 52 × 17
680 = 23 × 5 × 17
HCF = 2 × 5 × 17 = 170
Maximum capacity of the container = 170 liters.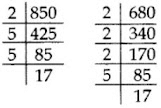
Q28: 144 cartons of Coke cans and 90 cartons of Pepsi cans are to be stacked in a canteen. If each stack is of the same height and if it equal contain cartons of the same drink, what would be the greatest number of cartons each stack would have?
Ans: The required answer will be HCF of 144 and 90.
144 = 24 × 32
90 = 2 × 32 × 5
HCF (144, 90) = 2 × 32 = 18
Thus each stack would have 18 cartons.
Q29: If p is prime number, then prove that √p is an irrational.
Ans: Let p be a prime number and if possible, let √p be rational
Thus,
√p = mn
where m and n are co-primes and n ≠0 .
Squaring on both sides, we get
p = m2n2
or, pn2 = m2 ...(1)
Here p divides pn2. Thus p divides m2 and in result p also divides m.
Let m = pq for some integer q and putting m = pq in eq. (1), we have
pn2 = p2q2
or, n2 = pq2
Here, p divides pq2. Thus p divides n2 and in result p also divides n.
[∵ p is prime and p divides n2 ⇒ p divides n]
Thus p is a common factor of m and n but this contradicts the fact that m and n are primes. The contradiction arises by assuming that √p is rational.
Hence, √p is irrational.
Q30: Amita, Sneha, and Raghav start preparing cards for all persons of an old age home. In order to complete one card, they take 10, 16 and 20 minutes respectively. If all of them started together, after what time will they start preparing a new card together?
Ans: To find the earliest (least) time, they will start preparing a new card together, we find the LCM of 10, 16 and 20.
10 = 2 × 5
16 = 24
20 = 22 × 5
LCM = 24 × 5 = 16 × 5 = 80 minutes
They will start preparing a new card together after 80 minutes.
Q31: If two positive integers x and y are expressible in terms of primes as x = p2q3 and y = p3q, what can you say about their LCM and HCF. Is LCM a multiple of HCF? Explain.
Ans: x = p2q3 and y = p3q
LCM = p3q3
HCF = p2q …(i)
Now, LCM = p3q3
⇒ LCM = pq2 (p2q)
⇒ LCM = pq2 (HCF)
Yes, LCM is a multiple of HCF.
Explanation:
Let a = 12 = 22 × 3
b = 18 = 2 × 32
HCF = 2 × 3 = 6 …(ii)
LCM = 22 × 32 = 36
LCM = 6 × 6
LCM = 6 (HCF) [From (ii)]
Here LCM is 6 times HCF.
Q32: Show that any positive odd integer is of the form 4q + 1 or 4q + 3 where q is a positive integer.
Ans: Let a be a positive odd integer
By Euclid’s Division algorithm:
a = 4q + r …[where q, r are positive integers and 0 ≤ r < 4]
a = 4q
or 4q + 1
or 4q + 2
or 4q + 3
But 4q and 4q + 2 are both even
a is of the form 4q + 1 or 4q + 3.
Long AnsweType Questions
Q33: Prove that √5 is an irrational number.
Ans: Assume that √5 be a rational number then we have
√5 = a/b
where a and b are co-primes and b≠0.
a = b√5
Squaring both the sides, we have
a2 = 5b2
Thus 5 is a factor of a2 and in result 5 is also a factor of a.
Let a = 5c where c is some integer, then we have
a2 = 25c2
Substituting a2 = 5b2 we have,
5b2 = 25c2
⇒ b2 = 5c2
Thus 5 is a factor of b2 and in result 5 is also a factor of b.
Thus √5 is a common factor of a and b. But this contradicts the fact that a and b are co-primes. Thus, our assumption that √5 is rational number is wrong.
Hence, √5 is irrational.
Q34: Prove that n2 - n is divisible by 2 for every positive integer n.
Ans: We have n2 - n = n(n-1)
Thus n2 - n is product of two consecutive positive integers.
Any positive integer is of the form 2q or 2q + 1, for some integer q.
Case 1: n = 2q
If n = 2q we have
n(n-1) = 2q(2q-1)
= 2m
where m = q(2q-1) which is divisible by 2.
Case 2: n = 2q+1
If n = 2q+1, we have
n(n-1) = (2q+1) (2q+1-1)
= 2q(2q+1)
= 2m
where m = q(2q+1) which is divisible by 2.
Hence, n2 - n is divisible by 2 for every positive integer n.
Case Based Type Questions
A. Read the following text and answer the following questions on the basis of the same:
To enhance the reading skills of grade X students, the school nominates you and two of your friends to set up a class library. There are two sections- section A and section B of grade X. There are 32 students in section A and 36 students in section B.
B. Read the following text and answer the following questions on the basis of the same:
A garden consists of 135 rose plants planted in certain number of columns. There are another set of 225 marigold plants, which is to be planted in the same number of columns.
|
129 videos|736 docs|84 tests
|
FAQs on Class 10 Maths Chapter 1 Important Question Answers - Real Numbers
| 1. What are real numbers and how are they classified? |  |
| 2. How do you find the least common multiple (LCM) and greatest common divisor (GCD) of two numbers? |  |
| 3. What is the difference between rational and irrational numbers? |  |
| 4. How can real numbers be represented on a number line? |  |
| 5. Why are real numbers important in mathematics and everyday life? |  |





















