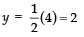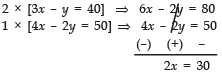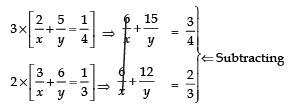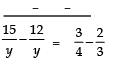Class 10 Maths Chapter 3 Question Answers - Pair of Linear Equations in Two Variables
Q1: A social welfare society donates a certain monthly amount towards the education of students from an economically weaker section with a fixed increment every year. The donation after 4 years was ₹ 15000 and ₹ 18000 after 10 years.
(i) What was the starting donation?
(ii) What is the annual increment?
(iii) Which mathematical concept is used in the above problem?
(iv) By contributing monthly financial help to students of EWS, which value is depicted by the social welfare society?
(i) Let the starting contribution be ₹ x and the fixed annual increment be
₹ y.
∴ Contribution after 4 years from the starting contribution = ₹(x + 4y)
Contribution after 10 years from the starting contribution = ₹(x + 10y)
⇒ We have,
x + 4y = 15000 ...(1)
x + 10y = 18000 ...(2)
Subtracting (1) from (2),x + 10y = 18000
x + 4y = 15000
6y = 3000⇒ y = 3000/6 = 500
Substituting y = 500 in (1), we have
x + 4(500) = 15000
⇒ x + 2000 = 15000
⇒ x = 15000 – 2000 = 13000
Thus, the starting donation was ₹ 13000.
(ii) ∵ y = 500
∴ The annual increment is ₹ 500
(iii) Pair of Linear Equations in two Variables
(iv) Charity
Q2: The ratio of pocket money of two students is 7: 9 and the ratio of their expenditures is 3: 4. If each of them saves ₹ 200 per month for donation to a Blind school.
(i) Find their respective pocket money and amount of donation.
(ii) Which mathematical concept is used in the above problem?
(iii) By donating their saving from pocket money to Blind school, which value is depicted by the students?
(i) Let the pocket money of the first student be ₹ 7x and that of the second student be ` 9x.
Let the expenditure of the first student be ₹ 3y and that of the second student be 4y.
∴ Saving of the first student = 7x – 3y
Saving of the second student = 9x – 4y
Solving the set of above simultaneous equations, we have :
4 × [7x – 3y = 200]
⇒ 28x – 12y = 800 ...(1)
3 × [9x – 4y = 200]
⇒ 27x – 12y = 600 ... (2)
Subtracting (2) from (1),28x - 12y = 800
27x - 12y = 600
( - ) ( + ) ( - )
x + 0y = 200⇒ x = 200
Substituting
x = 200, in 7x – 3y = 200, we get
7 × 200 – 3y = 200
⇒ 1400 – 3y = 200
⇒ –3y = 200 – 1400 = –1200
⇒ y = -1200/-3 = 400
Now, 7x = 7 × 200 = 1400; 9x = 9 × 200 = 1800 and donation = ₹ 200 each
∴ Pocket money of first student = ₹ 1400
Pocket money of second student = ₹ 1800
(ii) Pair of Linear Equations in two variable.
(iii) Charity
Q3: The progressive club helps needy students by giving free textbooks and stationery items. The club purchased 5 books and 7 pens together cost ₹ 79 whereas 7 book and 5 pens together cost ₹ 77.
(i) Find the total cost of 100 books and 100 pens.
(ii) Which mathematical concept is used in the above problem?
(iii) By donating books and stationery items to needy students which value is depicted by progressive-club?
(i) Let the cost of one book be ₹ x and that of one pen be ₹ y.
∴ Cost of 5 books + cost of 7 pen = ₹ 79
⇒ 5x + 7y = 79 ...(1)
Also, cost of 7 books + cost of 5 pens
= ₹ 77
⇒ 7x + 5y = 77 ...(2)
To solve (1) and (2), we have
5x + 7y = 79
7x + 5y = 77
⇒ 7 × [5x + 7y = 79]
⇒ 5 × [7x + 5y = 77]
⇒ 35x + 49y = 553 ...(3)
35x + 25y = 385 ...(4)Subtracting (4) from (3), we have
24y = 168 ⇒ y = 168/24 = 7
Substituting y = 7 in (1),
5x + (7 × 7) = 79
5x + 49 = 79
5x = 79 – 49 = 30
⇒ x = 30/5 = 6
i.e. cost of 100 books = ₹ 7 ×100 = ₹ 700
cost of 100 pens = ₹ 6 × 100 = ₹ 600
⇒ cost of 100 books + cost of 100 pens = ₹ 700 + ₹ 600 = ₹ 1300
(ii) Pair of Linear Equations in two variables.
(iii) Charity.
Q4: Aniket saves some amount daily from his pocket money. He saved ₹ 200 and gave to his younger sister Akhila, who wished to enjoy a fair. She wanted to enjoy rides on the Giant-Wheel and play Hoopla (a game in which you throw a ring on the items kept in a stall, and if the ring covers any object completely, you get it). The number of times she played Hoopla is half the number of rides she had on the Giant wheel.
(i) If each ride costs ₹ 30 and a game of Hoopla costs ₹ 40, find the number of rides she had and the number of times she played Hoopla, provided she spent ₹ 200?
(ii) Which mathematical concept is used in the above problem?
(iii) By saving and giving the amount from his pocket money, which value is depicted by Aniket?
(i) Let the number of rides that Akhila had = x
And number of times Akhila played Hoopla = y
∴ According to the condition, we get
y =....(1)
and ..(2)
Solving (1) and (2), we have30x + 20x = 20
⇒50x = 200
x = 200/50 = 4
Again, substituting, x = 4 in (1), we get
Thus, the required number of rides is 2 and the number of Hoopa plays is 4.
(ii) Pair of Linear Equations in Two Variables.
(iii) Savings to give happiness to youngers.
Q5: Mr Ajay, the mathematics teacher encouraged 40 of his class X students to take part in a Mathematics quiz. If the number of girls is 4 more than the number of boys.
(i) Find the number of boys and girls who took part in the quiz.
(ii) Which mathematical concept is used in the above problem?
(iii) By encouraging the students to take part in quiz-contest, which value is depicted by Mr Ajay, the mathematics teacher?
(i) Let the number of boys be x and the number of girls be y
∴ 3x + 7y = 14
∴ x + y = 40 ...(1)
According to the condition
[Number of girls] = [Number of boys] + 4
⇒ y = x + 4
or x – y = –4 ...(2)
Solving (1) and (2),x + y = 40
Adding (1) and (2)
x - y = -42x = 36 ⇒ x = 362 = 18
From (1), x + y = 40
⇒ 18 + y = 40
⇒ y = 40 - 18 = 22
Thus,
The number of boys = 18
The number of girls = 22
(ii) Pair of Linear Equations in two variables.
(iii) Competitive spirit.
Q6: Mrs Sharma is a housewife, she arranges a mathematics test for her daughter every Sunday. Her daughter scored 40 marks in one of such test receiving 3 marks for each right answer and losing 1 mark for each wrong answer. Had 4 marks been awarded for each correct answer and 2 marks been deducted for each incorrect answer, then her daughter would have scored 50 marks.
(i) How many questions were there in the test?
(ii) Which mathematical concept is used in the above problem?
(iii) By giving a test to her daughter (with negative marking) every Sunday which value is depicted by Mrs Sharma?
(i) Let the number of questions attempted with correct answer = x.
Let the number of questions attempted with wrong answer = y.
Case I: Marks awarded for 1 correct answer = 3
Marks deducted for 1 wrong answer = 1
∴Total marks obtained = 3x – y
3x – y = 40 ...(1)
Case II: Marks awarded for 1 correct answer = 4
Marks deducted for 1 wrong answer = 2
∴Total marks = 4x – 2y
⇒ 4x – 2y = 50 ...(2)
To solve (1) and (2), we have
⇒ x = 30/2 = 15
From (1), we have
3x – y = 40 ⇒ 3(15) – y = 40
⇒ 45 – y = 40
⇒ y = 45–40 = 5
Thus, number of questions attempted correct = 15
number of questions attempted incorrect = 5
⇒ Total number of questions in the test = 15 + 5 = 20
(ii) Simultaneous equations in two variables.
(iii) Competitive spirit.
Q7: A group of people take a voluntary decision to undertake a community task 2 women and 5 men of them can together finish the task in 4 days whereas 3 women and 6 men can finish the same task in 3 days.
(i) Find the time taken by 1 woman alone to finish the task.
(ii) Find the time taken by 1 man alone to finish the task
(iii) By taking a decision to do a community task, which value is depicted by the group of people.
(i) Let one woman can finish the task in x days.
Let one man can finish the task in y days.
∴ Part of work finished by a woman in 1 day = 1/x.
Part of work finished by a man in 1 day = 1/y.
∴ (2 women’s 1-day work) + (5 men’s 1-day work) = 1/4
∵ They together finish the work in 4 days.
⇒...(1)
Also (3 women’s 1 day work) + (6 men’s 1 day work) = 1/3 ...(2)...(2)
Solving (1) and (2), we have
⇒
⇒ 3/y = 1/12
⇒ y = 3 × 12 = 36 daysSubstituting y = 36 in (2), we get
3x + 636 = 13
⇒ 3x - 13 = 636 = 16
⇒ 3x = 2 - 16 = 16
⇒ x = 6 × 3 = 18 days
Thus, one man can alone finish the task in 36 days.
(ii) And one woman can alone finish the task in 18 days.
(iii) Community service.
Q8: Mr Saini is a retired person. He has set up a library for lending books and donates the proceeds to an orphanage. His library has a fixed charge for the first three days and an additional charge for each day thereafter. Saritha paid ₹ 27 for a book kept for 7 days, while Susy paid ₹ 21 for the book she kept for 5-days.
(i) Find the fixed charge and the charge for each extra day.
(ii) Which mathematical concept is used in the above problem?
(iii) By donating the proceeds to an orphanage, which value is depicted by Mr Saini?
(i) Let the fixed charge for the first three days = ₹ x
Let the charge for each extra day = ₹ y
For Saritha
[Amount for first 3 days] + [Amount for next 4 days] = ₹ 27
⇒ x + 4y = 27 ...(1)
For Susy
[Amount for first 3 days] + [Amount for 2 extra days] = ₹ 21
⇒ x + 2y = 21 ...(2)
Solving (1) and (2) we get
Substituting y = 3 in (1), we have
x + 4(3) = 27
⇒ x + 12 = 27
⇒ x = 27 – 12 = 15
Thus, fixed charge = ₹ 15
Charges for each extra day = ₹ 3
(ii) Pair of Linear equations in two variables.
(iii) Charity.
Q9: In a school charity drive, students collected donations. The total number of donations received from two classes was ₹ 4000. Class A contributed ₹ 500 more than Class B.
(i) Find the donation amounts from Class A and Class B.
(ii) Which mathematical concept is used in the above problem?
(iii) By participating in the charity drive, which value is depicted by the students?
(i) Let the donation amount from Class A be ₹ x and from Class B be ₹ y.
Given:
x + y = 4000 ... (1)
According to the condition:
Class A’s donation = Class B’s donation + 500
x = y+500
or,
(y+500) + y = 4000
Solving the equation,
2y+500=4000 ⇒2y=3500 ⇒y=1750
Substituting y=1750 in equation (1),
x+1750 = 4000 ⇒ x=2250
Thus,
Donation from Class A = ₹ 2250
Donation from Class B = ₹ 1750
(ii) Pair of Linear Equations in Two Variables.
(iii) Generosity and Social Responsibility.
Q10: A farmer divided his field into two plots. The total area of the two plots was 400 square meters. The area of the second plot was 50 square meters less than twice the area of the first plot.
(i) Find the areas of both plots.
(ii) Which mathematical concept is used in the above problem?
(iii) By utilizing the land effectively, which value is depicted by the farmer?
(i) Let the area of the first plot be x square meters and the area of the second plot be y square meters.
Given:
x + y = 400 ... (1)
According to the condition:
= 2 × Area of first plot − 50
y = 2x−50
or,
x + (2x−50) = 400
Solving the equation,
3x − 50 = 400 ⇒ 3x = 450 ⇒ x = 150
Substituting x=150 in equation (1),
x + y=400 ⇒150+y=400 ⇒y=250
Thus,
Area of first plot = 150 square meters
Area of second plot = 250 square meters
(ii) Pair of Linear Equations in Two Variables.
(iii) Efficient Resource Management and Sustainability.
|
127 videos|584 docs|79 tests
|
FAQs on Class 10 Maths Chapter 3 Question Answers - Pair of Linear Equations in Two Variables
| 1. What are pair of linear equations in two variables? |  |
| 2. How can we solve a pair of linear equations graphically? |  |
| 3. What methods can be used to solve a pair of linear equations algebraically? |  |
| 4. What is the significance of the determinant in solving linear equations? |  |
| 5. How do we interpret the solution of a pair of linear equations in real-life scenarios? |  |