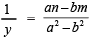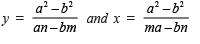Class 9 Maths Chapter 4 HOTS Questions - Linear Equations in Two Variables
Q1. Solve:
Hint: 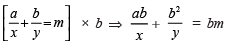 ...(1)
...(1)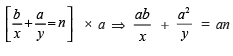 ...(2)
...(2)
Sol.
Subtracting (1) from (2),
= an – bm or
Thus,
Ans.
Q2. Solve : 141x + 103y = 217; 103x + 141y = 27
Sol. 141x + 103y = 217 .......... (i)
103x + 141y = 27......... (ii)
(i) × 141 - (ii) × 103
(141)2x + (103)(141)y = 217 × 141
(130)2x + (103)(141)y = 27 × 103
Subtracting both equations, we get
x= (217 x 141)-(27 x 103)/ 1412- 1032
x=3
From equation (i)
141 x 3+ 103 x y=217
y= -2
Q3. Cost of a pen is two and half times the cost of a pencil. Express this situation as a linear equation in two variables.
Sol. Let cost of a pen be ₹ x and cost of a pencil be ₹ y. According to statement of the question, we have x = 5/2 y ⇒ 2x = 5y or 2x – 5y = 0
Q4. Show that the points A (1, 2), B ( – 1, – 16) and C (0, – 7) lie on the graph of the linear equation y = 9x – 7.
Sol.
We have the equation,
y = 9x – 7
For A (1, 2),
Substituting (x,y) = (1, 2),
We get,
2 = 9(1) – 7
2 = 9 – 7
2 = 2
For B (–1, –16),
Substituting (x,y) = (–1, –16),
We get,
–16 = 9(–1) – 7
-16 = – 9 – 7
-16 = – 16
For C (0, –7),
Substituting (x,y) = (0, –7),
We get,
– 7 = 9(0) – 7
-7 = 0 – 7
-7 = – 7
Hence, the points A (1, 2), B (–1, –16) and C (0, –7) satisfy the line y = 9x – 7.
Thus, A (1, 2), B (–1, –16) and C (0, –7) are solutions of the linear equation y = 9x – 7
Therefore, the points A (1, 2), B (–1, –16), C (0, –7) lie on the graph of linear equation y = 9x – 7.
Q5. Solve : x + y = 18; y + z = 12; z + x = 16
Sol.
x+y = 18 ; y+z = 12 ;z+x = 16.x = 18-y ∴ z+18-y = 16 ⇒ y-z = z & y + z = 12adding -2y=14⇒y = 7 & z = 5∴ x = 18-7 = 11∴ x = 11, y = 7 & z = 5
Q6. Write four solutions for the following equation:
πx + y = 9
Sol. To find the four solutions of πx + y = 9 we substitute different values for x and y
Let x = 0
Then,
πx + y = 9
(π × 0)+y = 9
y = 9
(0,9)
Let x = 1
Then,
πx + y = 9
(π×1)+y = 9
π+y = 9
y = 9-π
(1,9-π)
Let y = 0
Then,
πx + y = 9
πx +0 = 9
πx = 9
x =9/π
(9/π,0)
Let x = -1
Then, πx + y = 9
(π(-1))+y = 9
-π + y = 9
y = 9+π
(-1,9+π)
The solutions are (0,9), (1,9-π),(9/π,0),(-1,9+π)
|
40 videos|419 docs|51 tests
|
FAQs on Class 9 Maths Chapter 4 HOTS Questions - Linear Equations in Two Variables
| 1. What is a linear equation in two variables? |  |
| 2. How do you graph a linear equation in two variables? |  |
| 3. What is the slope-intercept form of a linear equation? |  |
| 4. How can you determine if two linear equations in two variables are parallel? |  |
| 5. Can a linear equation in two variables have more than one solution? |  |