Q1: The unit of correlation coefficient between height in feet and weight in kgs is
(i) kg/feet
(ii) percentage
(iii) non-existent
Ans: The correlation coefficient between height in feet and weight in kilograms is a dimensionless quantity, meaning it has no units. The correlation coefficient can take values from -1 to 1. A value of 0 indicates no correlation between the two variables. Thus, the correct interpretation is that there is no existing correlation between height and weight in this context.
Q2: The range of simple correlation coefficient is
(i) 0 to infinity
(ii) minus one to plus one
(iii) minus infinity to infinity
Ans: The range of the simple correlation coefficient is from –1 to +1. This means that the value of the correlation coefficient, denoted as r, can vary between these two limits. A value of r equal to 1 indicates a perfect positive correlation, while a value of –1 indicates a perfect negative correlation. If r is 0, it suggests no linear relationship between the variables.
Q3: If rxy is positive the relation between X and Y is of the type
(i) When Y increases X increases
(ii) When Y decreases X increases
(iii) When Y increases X does not change
Ans: When the variables Y and X share positive relationship (i.e. when Y and X both increases simultaneously), then the value of rxy is positive.
Q4: If rxy = 0 the variable X and Y are
(i) linearly related
(ii) not linearly related
(iii) independent
Ans: The value of rxy equals 0 when the two variables are not linearly related. This means that while there is no linear relationship, the variables may still be related in a non-linear way. Therefore, a value of 0 does not imply that the variables are independent of each other.
Q5: Of the following three measures which can measure any type of relationship
(i) Karl Pearson’s coefficient of correlation
(ii) Spearman’s rank correlation
(iii) Scatter diagram
Ans: The scatter diagram is a versatile tool that can illustrate any type of relationship between two variables, regardless of how closely they are related. By examining the diagram, one can easily discern the nature of the relationship. In contrast, Karl Pearson's coefficient of correlation is not appropriate for series where deviations are calculated from an assumed mean. Similarly, Spearman's rank correlation is limited to qualitative variables and cannot measure relationships involving quantitative variables.
Q6: If precisely measured data are available the simple correlation coefficient is
(i) more accurate than rank correlation coefficient
(ii) less accurate than rank correlation coefficient
(iii) as accurate as the rank correlation coefficient
Ans: The simple correlation coefficient is generally more accurate than the rank correlation coefficient when precisely measured data are available. This is because the rank correlation coefficient typically yields a lower or equal value compared to the simple correlation coefficient. The main reason for this difference is that the rank correlation uses ranks instead of the full set of observations, which can result in a loss of information. When data is precisely measured, both coefficients will be identical. Therefore, if accurate measurements are available, the simple correlation coefficient is preferred due to its ability to utilise all available data.
Q7: Why is r preferred to covariance as a measure of association?
Ans: Although the correlation coefficient is similar to covariance in that both measure the degree of linear relationship between two variables, the former is generally preferred for several reasons. The value of the correlation coefficient (r) ranges from -1 to +1, expressed as -1 ≤ r ≤ +1. This range makes it easier to interpret the strength and direction of the relationship. Additionally, the correlation coefficient is scale-free, meaning it does not depend on the units of measurement used for the variables. This allows for comparisons between different datasets without concern for differing scales.
Q8: Can r lie outside the –1 and 1 range depending on the type of data?
Ans: No, the value of r cannot lie outside the range of –1 to 1. If r = – 1, then there exists perfect negative correlation and if r = 1, then there exists perfect positive correlation between the two variables. If at any point of time the calculated value of r is outside this range, then there must be some mistake committed in the calculation.
Q9: Does correlation imply causation?
Ans: No, correlation does not imply causation. Just because two variables are correlated does not mean that one causes the other. In simpler terms, a correlation indicates a relationship between the two variables, but it does not establish a cause-and-effect link. Correlation measures how two variables change together. If one variable increases, the other may also increase (a positive correlation) or decrease (a negative correlation). However, this does not mean that the change in one variable is responsible for the change in the other. In summary, correlation only shows the strength and direction of a relationship, not whether one variable causes the other to change.
Q10: When is rank correlation more precise than simple correlation coefficient?
Ans: The Rank Correlation method is more precise than the simple correlation coefficient when the variables cannot be measured quantitatively. This method assesses the correlation between two qualitative variables by assigning ranks based on preferences. For instance, in a dance competition, judges award ranks to candidates based on their preferences. Additionally, the rank correlation method is preferred when extreme values are present in the data, as the simple correlation coefficient may be misleading in such cases. The rank correlation provides a more reliable measure of association when dealing with qualitative data or when outliers could distort the results.
Q11: Does zero correlation mean independence?
Ans: Correlation measures the linear relationship between two variables. When r equals 0, it indicates that there is no linear relationship between the variables. However, this does not rule out the possibility of a non-linear relationship. Therefore, the absence of correlation does not imply that the two variables are independent.
Q12: Can a simple correlation coefficient measure any type of relationship?
Ans: No, the simple correlation coefficient cannot measure any type of relationship. It only assesses the direction and magnitude of a linear relationship between two variables. This means it cannot effectively evaluate non-linear relationships, such as quadratic, trigonometric, or cubic ones. In such cases, the simple correlation coefficient is inadequate. For instance, if we consider the equation X = Y2, the simple correlation coefficient may suggest that X and Y are not correlated, leading to the incorrect conclusion that the two variables are independent.
Q13: Collect the price of five vegetables from your local market every day for a week. Calculate their correlation coefficients. Interpret the result.
Ans: This question is about multivariate correlation that is out of syllabus
Q14: Measure the height of your classmates. Ask them the height of their benchmate. Calculate the correlation coefficient of these two variables. Interpret the result.
Ans:



Q15: List some variables where accurate measurement is difficult.
Ans: The following are some variables where accurate measurement is difficult.
- Temperature and number of people falling ill.
- Change in temperature with the height of a mountain.
- Low rainfall and agricultural productivity
- High population growth and degree of poverty
- Number of tourists and change in the political atmosphere in India.
Q16: Interpret the values of r as 1, –1 and 0.
Ans: The value of r being 1 indicates a perfect positive correlation between the two variables. This means that as one variable increases, the other also increases in a consistent manner. A high value of r (close to 1) signifies a strong positive linear relationship. If r equals -1, it denotes a perfect negative correlation. This implies that as one variable increases, the other decreases. A low value of r (close to -1) indicates a strong negative linear relationship between the variables. Conversely, if r equals 0, it suggests that the two variables are uncorrelated. This does not mean that the variables are independent; rather, it indicates that there is no linear relationship between them. However, they may still be related in a non-linear way.
Q17: Why does the rank correlation coefficient differ from the Pearsonian correlation coefficient?
Ans: The rank correlation coefficient differs from the Pearsonian correlation coefficient primarily due to the way they handle data. While both coefficients assess the relationship between two variables, the rank correlation coefficient typically yields a value that is lower than or equal to that of the Pearsonian coefficient. The rank correlation coefficient is particularly useful for measuring the correlation between two qualitative variables. In this context, the variables are assigned ranks based on preferences. This method results in a loss of information because it relies on ranks rather than the complete set of observations. When precise data is available, both coefficients will yield identical results. Another significant difference arises when extreme values are present in the data. The rank correlation coefficient is generally more robust in such cases, making it a more reliable measure compared to the Pearsonian coefficient. Thus, the presence of outliers can cause the two coefficients to differ significantly. In summary, the rank correlation coefficient is advantageous when dealing with qualitative data or when extreme values might skew results. It provides a clearer picture of relationships in these scenarios, while the Pearsonian coefficient is better suited for linear relationships with precise measurements.
Q18: Calculate the correlation coefficient between the heights of fathers in inches (X) and their sons (Y)
 Ans:
Ans:


Q19: Calculate the correlation coefficient between X and Y and comment on their relationship.
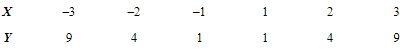 Ans:
Ans:


As the value of r is zero, so there is no linear correlation between X and Y
Q20: Calculate the correlation coefficient between X and Y and comment on their relationship
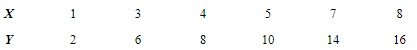 Ans:
Ans:

As the correlation coefficient between the two variables is +1, so the two variables are perfectly positively correlated.



 Ans:
Ans:

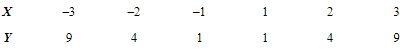 Ans:
Ans:

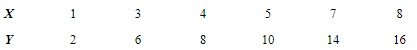 Ans:
Ans:























