Mohr Circle - Shear Strength of Soil, Soil Mechanics | Soil Mechanics Notes- Agricultural Engineering PDF Download
Mohr Circle
At any stressed point, three mutually perpendicular planes exist on which shear stress is zero. These planes are called principal planes. The normal stresses that act on these planes are called principal stress. The largest principal stress is called major principal stress (σ1), the lowest principal stress is called minor principal stress (σ3) and the third stress is called intermediate stress (σ2). The corresponding planes are called major, minor and intermediate plane, respectively. The critical stress values generally occur on the plane normal to the intermediate plane. Thus, only σ1 and σ3 are considered. Figure 9.2 shows an element and direction of σ1 and σ3. The major and minor principle planes are also shown. The major and minor principle planes are horizontal and vertical direction, respectively. The normal stress and shear stress at any plane making and angle q with horizontal can be determined analytically as:
\[\sigma={{{\sigma _1} + {\sigma _3}} \over 2} + {{{\sigma _1} - {\sigma _3}} \over 2}\cos 2\theta \] (9.3)
\[\tau={{{\sigma _1} - {\sigma _3}} \over 2}\sin 2\theta\] (9.4)
The stresses can be determined by graphically using Mohr Circle as shown in Figure 9.2. Mohr Circle is drawn in normal (σ) and shear (t) axis. The compressive normal stress is considered as positive. The shear stress that produces anti-clockwise couples on the element is considered as positive. The circle is drawn by taking O [(σ1 +σ3)/2, 0] as center and (σ1 -σ3)/2 as radius (as shown in Figure 9.2). Now from (σ3, 0) point draw a line parallel to AB plane. The line intersects the Mohr Circle at a point whose coordinates represents the normal and shear stress acting on AB plane [D(σ, t)]. The A (σ3, 0) point is called pole or the origin of plane.
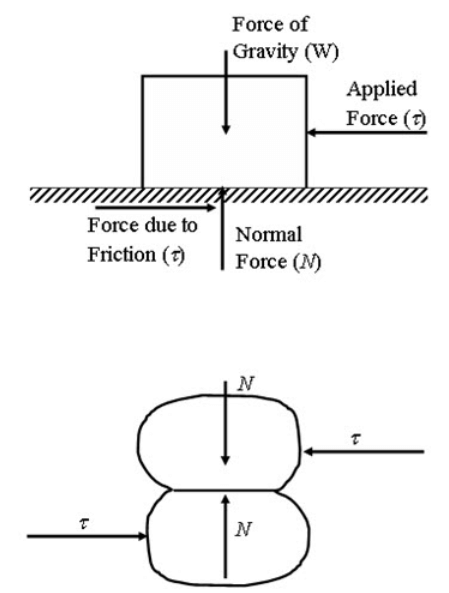
Fig. 9.1. Two particles/bodies in contact.
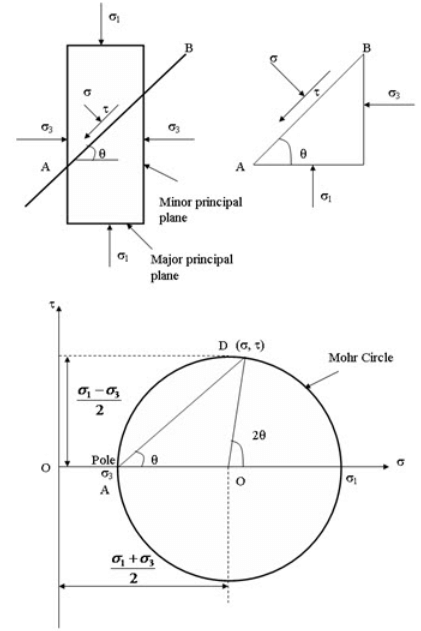
Fig. 9.2. Mohr Circle.
FAQs on Mohr Circle - Shear Strength of Soil, Soil Mechanics - Soil Mechanics Notes- Agricultural Engineering
| 1. What is Mohr Circle and how is it used in soil mechanics? |  |
| 2. What factors affect the shear strength of soil? |  |
| 3. How can the Mohr Circle be used to determine the shear strength of soil? |  |
| 4. What is the significance of the angle of internal friction in soil mechanics? |  |
| 5. How does the shear strength of soil impact agricultural engineering practices? |  |





















