Solved Examples: Units & Dimensions | Mock Tests for JEE Main and Advanced 2026 PDF Download
Problem 1:-
The Speed of Sound V in a Gas might plausibly depend on the Pressure P, the Density Ρ, and the Volume V of the Gas. Use Dimensional Analysis To Determine The Exponents X, Y, And Z in the Formula
V = Cpxρyvz
where C is a dimensionless constant. Incidentally, The mks units of pressure are kilograms per meter per second squared.
Solution:-
Equating the dimensions of both sides of the above equation, we obtain
 A comparison of the exponents of [L], [M], and [T] on either side of the above expression yields,
A comparison of the exponents of [L], [M], and [T] on either side of the above expression yields,
1 = -x – 3y +3z
0 = x+y
-1 = -2x
The third equation immediately gives x = ½ ; the second equation then yields y = – ½ ; finally, the first equation gives z = 0. Hence,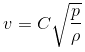
Problem 2:-
Milk is flowing through a full pipe whose diameter is known to be 1.8 cm. The only measure available is a tank calibrated in cubic feet, and it is found that it takes 1 h to fill 12.4 ft3.
What is the velocity of flow of the liquid in the pipe'?
Solution:-
velocity is [L]/[t] and the units in the SI system for velocity are therefore m s-1:
v = L/t where v is the velocity.
Now V = AL where V is the volume of a length of pipe L of cross-sectional area A
i.e. L = V/A.
Therefore v = V/At
Checking this dimensionally
[L][t]-1 = [L]3[L]-2[t]-1 = [L][t]-1
which is correct.
Since the required velocity is in m s-1, volume must be in m3, time in s and area in m2.
From the volume measurement
V/t = 12.4ft3 h-1
We know that,
1 ft3 = 0.0283 m3
1 = (0.0283 m3 /1 ft3)
1 h = 60 x 60 s
So, (1 h/3600 s) = 1
Therefore V/t = 12.4 ft3/h x (0.0283 m3/1 ft3) x (1 h/3600 s)
= 9.75 x 10-5 m3 s-1.
Also the area of the pipe A = πD2/4
= π(0.018)2 /4 m2
= 2.54 x 10-4 m2
v = V/t x 1/A
= 9.75 x 10-5/2.54 x 10-4
= 0.38 m s-1.
Problem 3:-
Force of viscosity F acting on a spherical body moving through a fluid depends upon its velocity (v), radius (r) and co-efficient of viscosity ‘η’ of the fluid. Using method of dimensions obtain an expression for ‘F’.
Solution:-
Let F ∝ va, F ∝ rb and F ∝ ηc …... (1)
So, F = Kvarbηc
where ‘K’ is a dimensional constant.
Dimensional formula of F = [M1L1T-2]
Dimensional formula of v = [L1T-1]
Dimensional formula of r = [L1]
Dimensional formula of η = [M1L-1T-1]
Substitute for the dimensional formulae in equation (1),
[M1L1T-2] = [L1T-1]a [L1]b [M1L-1T-1]c
[M1L1T-2] = [Mc La+b+c T-a-c] …... (2)
In accordance to principle of homogeneity, the dimensions of the two sides of relation (2) should be same.
So, c = 1 …... (3)
a+b-c = 1 …... (4)
-a – c = -2 …... (5)
Putting c = 1 in (5), we get a = 1
Putting a = 1 and c = 1 in (4), we get b = 1
Substituting for a, b and c in (1), F = kηrv, which is required relation.
|
517 docs|120 tests
|
FAQs on Solved Examples: Units & Dimensions - Mock Tests for JEE Main and Advanced 2026
| 1. What are the fundamental units of measurement in the metric system? |  |
| 2. How do dimensions affect physical quantities? |  |
| 3. Can units be converted between different systems of measurement? |  |
| 4. Why is it important to use proper units in scientific calculations? |  |
| 5. How are derived units formed in the metric system? |  |

















