Explore Exams
Login Signup
Sign in Open App
JEE Exam  >  JEE Notes  >  Mock Tests for JEE Main and Advanced 2026  >  Revision Notes - Sets, Relations & Functions

Relations and Functions Class 11 Notes Maths Chapter 1

  • Each element in a set is unique.         
  • The elements of a set may be discrete or continuous.
  • A set may contain no element at all, finite number of elements or infinite number of elements.
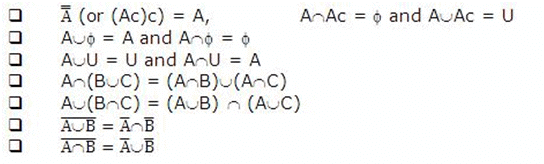
  • If A and B are two sets, then the following results hold true:Relations and Functions Class 11 Notes Maths Chapter 1
  • Relation is a linear operation which establishes relationship between the elements of two sets according to some definite rule of relationship.
  • If R is a relation from a set A to set B, then the set of all first components or coordinates of the ordered pairs is called the domain of R, while the set of all second components or coordinates of the ordered pairs is called as range of relation.
  • If R is a relation defined from A to B, then R-1 is a relation defined from B to A as R-1 = {(b,a)| (a, b) ∈ R}.
  • There can be various types of relations like:
  • Identity relation
  • Reflexive relation
  • Symmetric relation
  • Transitive relation
  • Equivalence relation
  • A relation defined on a set A is said to be an identity relation if every element of A is related to itself and only itself.
  • A relation such that (a, b) ∈ R then (a, a) ∈ R is reflexive. However, if there is a single ordered pair (a, b) ∈ R, such that (a, a) does not belong to R, then R is not reflexive.
  • A relation defined on a set is said to be symmetric if a R b ⇒ b R a.
  • A relation defined on a set A is said to be transitive if a R b and b R c then a R c.
  • A relation which is reflexive, symmetric as well as transitive is said to be an equivalence relation.
  • A relation becomes a function iff:
    To each a ∈ A, there exists a unique 'b' ∈ B such that (a, b) ∈ f.
    (a1, b1) ∈ f and (a1, b2) ∈ f ⇒ b1 = b2.
  • Let f : A → B, then the domain and codomain of f are defined as
    Domain of f = {a | a ∈ A, (a, f(a)) ∈ f}
    Range of f = {f(a) | a ∈ A, f(a) ∈ B, (a, f(a)) ∈ f}
  • Basic Properties of |x|:
    1. | |x| | = |x|
    2. |x| > a ⇒ x < a or x < -a if a ∈ R+ and x ∈ R if a ∈ R-
    3. |x| < a ⇒ -a < x <a if a ∈ R+ and no solution if a ∈ R- ∪ {0}
    4. |x + y| < |x| + |y|
    5. |x - y| > |x| - |y|
  • The last two properties can be put in one compact form namely,
    1. |x| - |y| < |x + y| < |x| + |y|
    2. |xy| = |x| |y|
    3. |x/y| = |x/y|, y ≠ 0
  • For ‘y’ to be an algebraic function of x it should satisfy an algebraic expression of the form P0(x)yn + P1(x)yn-1 + ….. + Pn-1(x)y + Pn(x) = 0
  • All polynomial functions are algebraic but every algebraic function need not be a polynomial function.
  • Signum Function:
    A function y = f(x) = Sgn (x) is defined as follows:
    y = f(x) = 1 for x > 0
    = 0 for x = 0
    = -1 for x < 0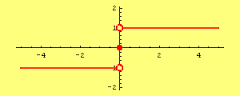
    Relations and Functions Class 11 Notes Maths Chapter 1
  • Properties of greatest integer function:
    1. [x] ≤ x < [x] + 1
    2. x-1 < [x] ≤ x
    3. [x+m] = [x] + m  if m is an integer
    4. [x] + [y] ≤ [x + y] ≤ [x] + [y] + 1
    5. [x] + [-x] = 0 if x is an integer
    = -1 otherwise 
  • Range of y = f(x) is the collection of all outputs corresponding to each real number of the domain. To find the range of a function:
    1. Find the domain of the function y = f(x) first.
    2. If domain is a set having only finite number of points, then range is the set of corresponding f(x) values.
    3. If domain of y = f(x) is R or R- {some finite points}, then express x in terms of y. from this, find y for x to be defined or form an equation in terms of x and apply the condition for real roots.
  • Two functions ‘f’ and ‘g’ are identical if and only if they satisfy the following conditions:
    1. Domain of f = Domain of g
    2. Range of f = Range of g
    3. f(x) = g(x) ∀x belonging to the common domain
  • If a function is entirely increasing or decreasing in some entire domain, then the function is one-to one.
  • If a line parallel to the x-axis cuts the graph of the function at a single point, then the function is one-to-one.
  • If a continuous function has at least one local maximum or local minimum, then the function is many-one.
  • A function can either be one-one or many-one but not both.
  • If range of a function f(x) = codomain of f(x), then the function f(x) is onto.
  • A polynomial function of even degree is always an into function.
  • A function can only be one of these four types:
    1. One-one onto (injective and surjective)
    2. One –one into (injective but not surjective)
    3. Many-one onto (surjective but not injective)
    4. Many-one into (neither injective nor surjective)
  • A continuous function which is always increasing or decreasing in the whole domain is one-one.
  • A function is one to one iff a horizontal line intersects its graph at most once.
  • If the range and co-domain for a function are same then it is onto.
  • If a set A contains ‘n’ distinct elements then the number of possible distinct functions from A to A is nn and out of these n! are one-one.
  • The range of a constant function is always a singleton.
  • A constant function may be one-one, many-one, onto or into.
  • If ‘f’ and ‘g’ are real valued functions with domains as A and B respectively, then both f and g are defined in A∩B.
    1. The domain of f + g, f-g and f.g is also A ∩ B.
    2. The domain of (f/g) is {x | x ∈A ∩ Bs.t. g(x) ≠ 0}.
  • For the product ‘gof’ of two functions f and g, the range of f must be a subset of the domain of g.
  • The composite of functions is not commutative, i.e. gof ≠ fog.
  • The composite of functions is associative i.e. if f, g and h are three functions such that fo(goh) = (fog)oh.
  • The composite of two bijections is a bijection i.e. if f and g are two bijections such that gof is defined then gof is also a bijection.
  • The inverse of a bijection is unique.
    1. If f: A→ B is a bijection, and g:B→ A is its inverse, then fog = IB and g of = IA, where IA and IB are the identities of A and B respectively.
    2. The graphs of f and g in this case are the mirror images of each other in the line y = x.
    3. The inverse of a bijection is also a bijection.
    4. If f and g are two bijections such that f: A→ B is a bijection, and g: B→ C, then the inverse of g of also exists and (fog)-1 = f -1og-1
  • The function is said to be even if f(x)-f(-x) = 0 and the function is said to be odd if f(x) + f(-x) = 0
    1. A function may neither be even nor odd.
    2. Inverse of an even function is not defined.
    3. Every even function is symmetric about the y-axis and every odd function is symmetric about origin.
    4. It is possible to express every function as the sum of an even and odd function i.e.
    f(x) = [{f(x) + f(-x)}/2 + {f(x)-f(-x)}/2], where the first part is an even function and the second part is the odd function.
    1. If function f and g are both even or both odd then the function f.g will be even but if either of them is odd then f.g will be odd.
    2. The only function which is defined on the entire number line and which is even as well as od at the same time is f(x) = 0.
  • The inverse of a periodic function does not exist.
    1. Every constant function is always periodic but with no fundamental period.
    2. If a function f(x) has period ‘T’ and the function g(x) also has the same period, then it is not necessary that the function f(x) + g(x) will also have ‘T’ as its period.
    3. If the function f has ‘p’ as its period then 1/f(x) and √f(x) also have p as the period.
  • If f(x) has period ‘T’ then f(ax+b) has a period T/a (a > 0).
  • Logarithm of a number to some base is the exponent by which the base must be raised in order to get that number.
  • Logarithm of zero does not exist and logarithm of negative reals is not defined in the system of real numbers.
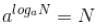  • Relations and Functions Class 11 Notes Maths Chapter 1is an identity for all N > 0 and a > , a ≠ 1.
  • The basic definition of logarithm yields the following results:
  • logNN = 1
  • log1/N N = -1
  • loga1 = 0
  • a logan =  n is an identity for all N > 0 and a > 0
  • Whenever the number and base are on the same side of unity then the logarithm of that number to the base is positive, but if the number and base are located on different side of unity, then the logarithm of that number to the base is negative.
  • Principal properties of logarithm:
    If m, n are arbitrary positive real numbers where a > 0, a ≠ 1
  • logam + logan = logamn
  • loga m/n = logam - logan
  • logamx = x logam
  • logamx = x logam
  • logax m = 1/x logam
  • Base changing theorem: It states that the quotient of the logarithm of two numbers is independent of their common base i.e.
    logca / logcb = logba
  • logba = 1/ logab
  • (logba).(logcb).(logdc) = logd a
  • alogbc = c logba
  • log10N is referred to as common logarithm and logeN is called the natural logarithm.
  • The common logarithm of a number consists of two parts, integral and fractional, of which the integral part may be zero or an integer (positive or negative) while the fractional part, a decimal less than 1 is always positive.
  • log x2n = 2n log |x|, where n ∈ I.
  • Note: Equations of the form [a(x)]b(x) = [a(x)]c(x) with the set of permissible values defined by the condition a(x) > 0, can be reduced to the equivalent equation
    b(x) logd[a(x)] = c(x) logd[a(x)] by taking logarithm of both sides. This equation hence is equivalent to the two equations logd[a(x)] = 0, b(x) = c(x).
The document Relations and Functions Class 11 Notes Maths Chapter 1 is a part of the JEE Course Mock Tests for JEE Main and Advanced 2026.
All you need of JEE at this link: JEE
357 docs|100 tests
Join Course for Free

FAQs on Relations and Functions Class 11 Notes Maths Chapter 1

1. What is a set in the context of Sets, Relations & Functions?
Ans. A set is a collection of distinct objects, called elements, that are well-defined and can be clearly identified. In Sets, Relations & Functions, sets are used to represent a group of related objects or elements.
2. What is the difference between a finite set and an infinite set?
Ans. A finite set is a set that contains a specific number of elements, which can be counted and listed. On the other hand, an infinite set is a set that contains an infinite number of elements, which cannot be counted or listed.
3. What is a relation in Sets, Relations & Functions?
Ans. A relation is a set of ordered pairs that establishes a connection or association between the elements of two different sets. It describes the relationship between the elements of the sets and can be represented using tables, graphs, or formulas.
4. How can functions be represented in Sets, Relations & Functions?
Ans. Functions in Sets, Relations & Functions can be represented using various methods, such as mapping diagrams, tables, graphs, or formulas. They show the relationship between the input values (domain) and the corresponding output values (range) in a clear and organized manner.
5. What is the difference between a one-to-one function and an onto function?
Ans. A one-to-one function, also known as an injective function, is a function where each element in the domain is mapped to a unique element in the range. In other words, no two different elements in the domain can be mapped to the same element in the range. An onto function, also known as a surjective function, is a function where every element in the range has at least one corresponding element in the domain. In other words, the range of the function covers the entire set of possible output values.
About this Document
4.87/5 Rating
Oct 10, 2025 Last updated
Related Exams
JEE
Document Description: Revision Notes - Sets, Relations & Functions for JEE 2025 is part of Mock Tests for JEE Main and Advanced 2026 preparation. The notes and questions for Revision Notes - Sets, Relations & Functions have been prepared according to the JEE exam syllabus. Information about Revision Notes - Sets, Relations & Functions covers topics like and Revision Notes - Sets, Relations & Functions Example, for JEE 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Revision Notes - Sets, Relations & Functions.
Introduction of Revision Notes - Sets, Relations & Functions in English is available as part of our Mock Tests for JEE Main and Advanced 2026 for JEE & Revision Notes - Sets, Relations & Functions in Hindi for Mock Tests for JEE Main and Advanced 2026 course. Download more important topics related with notes, lectures and mock test series for JEE Exam by signing up for free. JEE: Relations and Functions Class 11 Notes Maths Chapter 1
Description
Full syllabus notes, lecture & questions for Relations and Functions Class 11 Notes Maths Chapter 1 - JEE | Plus excerises question with solution to help you revise complete syllabus for Mock Tests for JEE Main and Advanced 2026 | Best notes, free PDF download
Information about Revision Notes - Sets, Relations & Functions
In this doc you can find the meaning of Revision Notes - Sets, Relations & Functions defined & explained in the simplest way possible. Besides explaining types of Revision Notes - Sets, Relations & Functions theory, EduRev gives you an ample number of questions to practice Revision Notes - Sets, Relations & Functions tests, examples and also practice JEE tests
Explore Courses for JEE exam
Related Searches

Semester Notes

,

shortcuts and tricks

,

Previous Year Questions with Solutions

,

video lectures

,

Sample Paper

,

pdf

,

Viva Questions

,

study material

,

ppt

,

past year papers

,

Extra Questions

,

Relations and Functions Class 11 Notes Maths Chapter 1

,

MCQs

,

Relations and Functions Class 11 Notes Maths Chapter 1

,

Relations and Functions Class 11 Notes Maths Chapter 1

,

mock tests for examination

,

Objective type Questions

,

Summary

,

practice quizzes

,

Free

,

Important questions

,

Exam

;
Additional Information about Revision Notes - Sets, Relations & Functions for JEE Preparation

Revision Notes - Sets, Relations & Functions Free PDF Download

The Revision Notes - Sets, Relations & Functions is an invaluable resource that delves deep into the core of the JEE exam. These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective. With the help of these notes, you can grasp complex subjects quickly, revise important points easily, and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner, allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material, or toppers' notes, this PDF has got you covered. Download the Revision Notes - Sets, Relations & Functions now and kickstart your journey towards success in the JEE exam.

Importance of Revision Notes - Sets, Relations & Functions

The importance of Revision Notes - Sets, Relations & Functions cannot be overstated, especially for JEE aspirants. This document holds the key to success in the JEE exam. It offers a detailed understanding of the concept, providing invaluable insights into the topic. By knowing the concepts well in advance, students can plan their preparation effectively. Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.

Revision Notes - Sets, Relations & Functions

Revision Notes - Sets, Relations & Functions Notes offer in-depth insights into the specific topic to help you master it with ease. This comprehensive document covers all aspects related to Revision Notes - Sets, Relations & Functions. It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation. Practice papers and question papers enable you to assess your progress effectively. Additionally, the paper analysis provides valuable tips for tackling the exam strategically. Access to Toppers' notes gives you an edge in understanding complex concepts. Whether you're a beginner or aiming for advanced proficiency, Revision Notes - Sets, Relations & Functions Notes on EduRev are your ultimate resource for success.

Revision Notes - Sets, Relations & Functions JEE Questions

The "Revision Notes - Sets, Relations & Functions JEE Questions" guide is a valuable resource for all aspiring students preparing for the JEE exam. It focuses on providing a wide range of practice questions to help students gauge their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation. The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level. Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.

Study Revision Notes - Sets, Relations & Functions on the App

Students of JEE can study Revision Notes - Sets, Relations & Functions alongwith tests & analysis from the EduRev app, which will help them while preparing for their exam. Apart from the Revision Notes - Sets, Relations & Functions, students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc. The EduRev App will make your learning easier as you can access it from anywhere you want. The content of Revision Notes - Sets, Relations & Functions is prepared as per the latest JEE syllabus.
© EduRev
Education Revolution
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup