JEE Exam > JEE Notes > Mock Tests for JEE Main and Advanced 2026 > Revision Notes - Complex Number
Complex Numbers and Quadratic Equations Class 11 Notes Maths Chapter 4
- z1 = a+ib and z2 = c+id then z1 = z2 implies that a = c and b = d.
- If we have a complex number z where z = a+ib, the conjugate of the complex number is denoted by z* and is equal to a-ib. In fact, for any complex number z, its conjugate is given by z* = Re(z) – Im(z).
- Division of complex numbers: The numerator as well as denominator should first be multiplied by the conjugate of the denominator and then simplified.
Argument of a complex number:
1. Argument of a complex number p(z) is defined by the angle which OP makes with the positive direction of x-axis.
2. Argument of z generally refers to the principal argument of z (i.e. the argument lying in (–π, π) unless the context requires otherwise.
3. Hence, the argument of the complex number z = a + ib = r (cos θ + i sin θ) is the value of θ satisfying r cos θ = a and r sin θ = b.
4. The angle θ is given by θ = tan-1 |b/a|.
5. The value of argument in various quadrants is given below:

- If OP = |z| and arg (z) = θ, then obviously z = r (cos θ + i sin θ) and is called the polar form of complex number z.
- |(z-z1)/(z-z2)| =1 the locus of point representing z is the perpendicular bisector of line joining z1 and z2.
- -|z| ≤ Re(z) ≤ |z| and -|z| ≤ Im(z) ≤ |z|
- If a and b are real numbers and z1 and z2 are complex numbers then
|az1 + bz2|2 + |bz1 - az2|2 = (a2 + b2) (|z1|2 + (|z2|2) - The distance between the complex numbers z1 and z2 is given by |z1 - z2|.
- In parametric form, the equation of line joining z1 and z2 is given by z = tz1 + (1-t)z2.
- If A(z1) and B(z2) are two points in the argand plane, then the complex slope μ of the straight line AB is given by μ = (z1 - z2)/ (1 - 2).
- Two lines having complex slopes μ1 and μ2 are:
1. Parallel iff μ1 = μ2
2. Perpendicular iff μ1 = - μ2 or μ1 + μ2 = 0 - If A(z1), B(z2), C(z3) and D(z4) are four points in the argand plane, then the angle θ between the lines AB and CD is given by θ = arg{(z1 - z2)/ (z3 – z4)}
- Some basic properties of complex numbers:
I. ||z1| - |z2|| = |z1+z2| and |z1-z2| = |z1| + |z2| iff origin, z1, and z2 are collinear and origin lies between z1 and z2.
II. |z1 + z2| = |z1| + |z2| and ||z1| - |z2|| = |z1-z2| iff origin, z1 and z2 are collinear and z1 and z2 lie on the same side of origin.
III. The product of nth roots of any complex number z is z(-1)n-1.
IV. amp(zn) = n amp z
V. The least value of |z - a| + |z - b| is |a - b|.
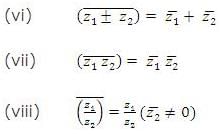 Demoivre's Theorem: The theorem can be stated in two forms:
Demoivre's Theorem: The theorem can be stated in two forms:
Case I: If n is any integer, then
(i) (cos θ + i sin θ)n = cos nθ + i sin nθ
(ii) (cos θ1 + i sin θ1) . (cos θ2 + i sin θ2) ......... (cos θn + i sin θn)
= cos (θ1 + θ2 + θ3 .................. + θn) + i sin (θ1 + θ2 + .............. θn)
Case II: For p and q such that q ≠ 0, we have
(cosθ + isinθ)p/q = cos((2kπ + pq)/q) + isin((2kπ+pq/q) where k = 0,1,2,3,.....,q-1- Demoivre’s formula does not hold for non-integer powers.
- Main application of Demoivre’s formula is in finding the nth roots of unity. So, if we write the complex number z in the polar form then,
z = r(cos x + isin x)
Then z1/n = [r (cos x +i sinx )]1/n
= r 1/n [ cos (x+2kπ/n) + i sin (x+2kπ/n)]
Here k is an integer. To get the n different roots of z one only needs to consider values of k from 0 to n –1 - Continued product of the roots of a complex quantity should be determined using theory of equations.
- The modulus of a complex number is given by |z| = √x2+y2.
- The only complex number with modulus zero is the number (0, 0).
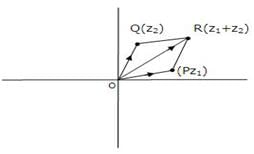
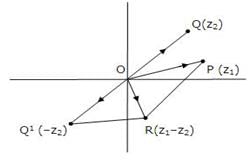
- The following figures illustrate geometrically the meaning of addition and subtraction of complex numbers:
The document Complex Numbers and Quadratic Equations Class 11 Notes Maths Chapter 4 is a part of the JEE Course Mock Tests for JEE Main and Advanced 2026.
All you need of JEE at this link: JEE
|
357 docs|100 tests
|
FAQs on Complex Numbers and Quadratic Equations Class 11 Notes Maths Chapter 4
| 1. What is the definition of a complex number? |  |
Ans. A complex number is a number that can be expressed in the form a + bi, where a and b are real numbers and i is the imaginary unit, defined as the square root of -1.
| 2. How do you add and subtract complex numbers? |  |
Ans. To add or subtract complex numbers, simply add or subtract the real and imaginary parts separately. For example, to add (3 + 2i) and (1 - 4i), add 3 and 1 to get 4, and add 2i and -4i to get -2i. Therefore, the sum is 4 - 2i.
| 3. What is the geometric interpretation of a complex number? |  |
Ans. A complex number can be represented as a point in a two-dimensional plane called the complex plane. The real part corresponds to the horizontal axis, while the imaginary part corresponds to the vertical axis. The magnitude of the complex number represents the distance from the origin, and the angle represents the direction.
| 4. How do you multiply complex numbers? |  |
Ans. To multiply complex numbers, use the distributive property and the fact that i^2 = -1. For example, to multiply (3 + 2i) and (1 - 4i), multiply 3 and 1 to get 3, multiply 3 and -4i to get -12i, multiply 2i and 1 to get 2i, and multiply 2i and -4i to get -8i^2. Simplify the expression and combine like terms to get the final result.
| 5. How do you find the conjugate of a complex number? |  |
Ans. The conjugate of a complex number a + bi is obtained by changing the sign of the imaginary part. In other words, the conjugate of a + bi is a - bi. For example, the conjugate of 3 + 2i is 3 - 2i. The conjugate is useful in various operations, such as dividing complex numbers and simplifying expressions involving complex conjugates.
Related Searches
















