JEE Exam > JEE Notes > Mock Tests for JEE Main and Advanced 2026 > Revision Notes - Solution of Triangles
Solution of Triangles Revision Notes | Mock Tests for JEE Main and Advanced 2026 PDF Download
- Sine rule: Sides of a triangle are proportional to the sine of the angles opposite to them. So, in ΔABC,
sin A/a = sin B/b = sin C/c = 2Δ/abc.
This may also be written as (a/sin A) = (b/sin B) = (c/sin C) - Cosine rule: In any ΔABC,
cos A = (b2 + c2 – a2) /2bc
cos B = (a2 + c2 – b2)/2ac
cos C = (a2 + b2 - c2)/2ab - Trigonometric ratios of half-angles:
sin A/2 = √[(s-b)(s-c)/bc]
sin B/2 = √[(s-c) (s-a)/ac]
sin C/2 = √[(s-a) (s-b)/ab]
cos A/2 = √s(s - a)/bc
cos B/2 = √s(s - b)/ac
cos C/2 = √s(s - c)/ab
tan A/2 = √[(s - b) (s - c)/s(s - a)]
tan B/2 = √[(s - c) (s - a)/s(s - b)]
tan C/2 = √[(s - a) (s - b)/s(s - c)] - Projection rule: In any ΔABC,
a = b cos C + c cos B
b = c cos A + a cos C
c = a cos B + b cos A - Area of a triangle
If Δ denotes the area of the triangle ABC, then it can be calculated in any of the following forms:
Δ = 1/2 bc sin A = 1/2 ca sin B = 1/2 ab sin C
Δ = √s(s - a)(s – b)(s - c)
Δ = 1/2. (a2 sin B sin C)/ sin(B + C)
= 1/2. (b2 sin C sin A)/ sin (C + A)
= 1/2. (c2 sin A sin B)/ sin (A + B) - Semi-perimeter of the triangle
If S denotes the perimeter of the triangle ABC, then s = (a + b + c)/2 - Napier’s analogy
In any ΔABC,
tan [(B – C)/2] = (b – c)/(b + c) cot A/2
tan [(C – A) /2] = (c – a)/(c + a) cot B/2
tan [(A – B) /2] = (a – b)/(a + b) cot C/2 - m-n theorem
Consider a triangle ABC where D is a point on side BC such that it divides the side BC in the ratio m: n, then as shown in the figure, the following results hold good: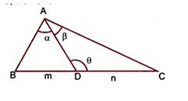
(m + n) cot θ = m cot α – n cot ß.
(m + n) cot θ = n cot B – m cot C. - Apollonius theorem
In a triangle ABC, if AD is the median through A, then
AB2 + AC2 = 2(AD2 + BD2). - If the three sides say a, b and c of a triangle are given, then angle A is obtained with the help of the formula
tan A/2 = √(s - b) (s - c) / s(s - a) or cos A = b2 + c2 - a2 / 2bc.
Angles B and C can also be obtained in the same way. - If two sides b and c and the included angle A are given, then
tan (B – C) /2 = (b – c)/ (b + c) cot A/2
This gives the value of (B- C)/2.
Hence, using (B + C)/2 = 90o - A/2 along with the last equation both B and C can be evaluated. Now, the sides can be evaluated using the formula
a = b sin A/sin B or a2 = b2 + c2 – 2bc cosA. - If two sides b and c and the angle B (opposite to side b) are given, then using the following results, we can easily obtain the remaining elements
sin C = c/b sinB, A = 180o – (B + C) and b = b sin A/sinB - Some of the important points which must be remembered include:
1. b < c sin B, there is no triangle possible (Fig. 1)
2. If b = c sin B and B is an acute angle, then only one triangle is possible (Fig. 2)
3. If c sin B < b < c and B is an acute angle, then there are two values of angle C (Fig. 3).
4. If c < b and B is an acute angle, then there is only one triangle (Fig. 4).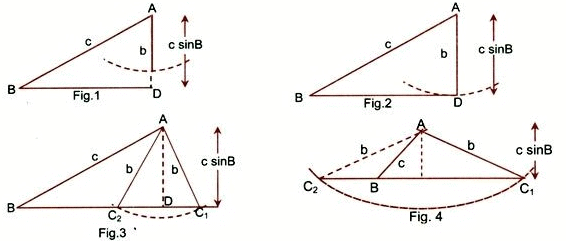
The document Solution of Triangles Revision Notes | Mock Tests for JEE Main and Advanced 2026 is a part of the JEE Course Mock Tests for JEE Main and Advanced 2026.
All you need of JEE at this link: JEE
|
357 docs|100 tests
|
FAQs on Solution of Triangles Revision Notes - Mock Tests for JEE Main and Advanced 2026
| 1. How do I solve a triangle using the given article's solution of triangles method? |  |
Ans. To solve a triangle using the given article's method, follow these steps:
1. Identify the given information: angles and sides of the triangle.
2. Determine which trigonometric ratio (sine, cosine, or tangent) to use based on the given information.
3. Apply the appropriate trigonometric ratio to find the missing angles or sides.
4. Repeat the process if necessary until all the angles and sides of the triangle are known.
5. Verify your solution by checking if the sum of all angles equals 180 degrees and if the triangle satisfies the triangle inequality theorem.
| 2. Can I solve a triangle with only two angles given? | |
Ans. No, it is not possible to solve a triangle with only two angles given. In order to fully solve a triangle, you need to know either three sides or two sides and the included angle, or two angles and the included side. This principle is based on the fact that the sum of the angles in a triangle is always 180 degrees. Without sufficient information, it is not possible to determine the lengths of the sides or the values of the angles accurately.
| 3. Are there any special cases in solving triangles? | |
Ans. Yes, there are special cases in solving triangles. Two commonly encountered special cases are the right-angled triangle and the equilateral triangle.
- In a right-angled triangle, one of the angles is 90 degrees. This allows for the use of special trigonometric ratios such as sine, cosine, and tangent.
- In an equilateral triangle, all three angles are equal to 60 degrees, and all three sides are equal in length. This symmetry simplifies the calculations and allows for the use of special trigonometric ratios.
| 4. Can I use the solution of triangles method to solve any type of triangle? | |
Ans. Yes, the solution of triangles method can be used to solve any type of triangle, including acute, obtuse, and right-angled triangles. The method is based on trigonometric ratios, which are applicable to all types of triangles. However, it is important to ensure that you have sufficient information (angles or sides) to apply the trigonometric ratios accurately. Otherwise, the triangle may not be solvable.
| 5. What is the significance of verifying the solution in solving triangles? | |
Ans. Verifying the solution is important in solving triangles to ensure the accuracy of the calculations and to confirm that the triangle is valid. By checking if the sum of all angles equals 180 degrees, you can confirm that your solution is consistent with the rules of geometry. Additionally, verifying the solution helps identify any errors or inconsistencies in the calculations, allowing you to correct them and arrive at the correct solution.
About this Document
1.2K Views
4.63/5
Rating
Oct 14, 2025
Last updated
Related Exams
Document Description: Revision Notes - Solution of Triangles for JEE 2025 is part of Mock Tests for JEE Main and Advanced 2026 preparation.
The notes and questions for Revision Notes - Solution of Triangles have been prepared according to the JEE exam syllabus. Information about Revision Notes - Solution of Triangles covers topics
like and Revision Notes - Solution of Triangles Example, for JEE 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Revision Notes - Solution of Triangles.
Introduction of Revision Notes - Solution of Triangles in English is available as part of our Mock Tests for JEE Main and Advanced 2026
for JEE & Revision Notes - Solution of Triangles in Hindi for Mock Tests for JEE Main and Advanced 2026 course.
Download more important topics related with notes, lectures and mock test series for JEE
Exam by signing up for free. JEE: Solution of Triangles Revision Notes | Mock Tests for JEE Main and Advanced 2026
Description
Full syllabus notes, lecture & questions for Solution of Triangles Revision Notes | Mock Tests for JEE Main and Advanced 2026 - JEE | Plus excerises question with solution to help you revise complete syllabus for Mock Tests for JEE Main and Advanced 2026 | Best notes, free PDF download
Information about Revision Notes - Solution of Triangles
In this doc you can find the meaning of Revision Notes - Solution of Triangles defined & explained in the simplest way possible. Besides explaining types of
Revision Notes - Solution of Triangles theory, EduRev gives you an ample number of questions to practice Revision Notes - Solution of Triangles tests, examples and also practice JEE
tests
Related Searches
Solution of Triangles Revision Notes | Mock Tests for JEE Main and Advanced 2026
,Sample Paper
,Exam
,past year papers
,Summary
,mock tests for examination
,Important questions
,Free
,video lectures
,practice quizzes
,shortcuts and tricks
,Objective type Questions
,Semester Notes
,Previous Year Questions with Solutions
,study material
,Solution of Triangles Revision Notes | Mock Tests for JEE Main and Advanced 2026
,Viva Questions
,Solution of Triangles Revision Notes | Mock Tests for JEE Main and Advanced 2026
,MCQs
,Extra Questions
,ppt
;
Additional Information about Revision Notes - Solution of Triangles for JEE Preparation
Revision Notes - Solution of Triangles Free PDF Download
The Revision Notes - Solution of Triangles is an invaluable resource that delves deep into the core of the JEE exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Revision Notes - Solution of Triangles now and kickstart your journey towards success in the JEE exam.
Importance of Revision Notes - Solution of Triangles
The importance of Revision Notes - Solution of Triangles cannot be overstated, especially for JEE aspirants.
This document holds the key to success in the JEE exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Revision Notes - Solution of Triangles
Revision Notes - Solution of Triangles Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Revision Notes - Solution of Triangles.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Revision Notes - Solution of Triangles Notes on EduRev are your ultimate resource for success.
Revision Notes - Solution of Triangles JEE Questions
The "Revision Notes - Solution of Triangles JEE Questions" guide is a valuable resource for all aspiring students preparing for the
JEE exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Revision Notes - Solution of Triangles on the App
Students of JEE can study Revision Notes - Solution of Triangles alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Revision Notes - Solution of Triangles,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Revision Notes - Solution of Triangles is prepared as per the latest JEE syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup