JEE Exam > JEE Notes > Mock Tests for JEE Main and Advanced 2025 > Revision Notes - Trigonometric Functions
Trigonometric Functions Class 11 Notes Maths Chapter 3
- The trigonometric ratios are the ratios between the two sides of a right-angles triangle with respect to an angle and hence they are real numbers.
- The angle θ taken into consideration may be acute, obtuse or right angle.
- Various trigonometry formulas related to the basic trigonometric ratios which must be remembered include:
1) sin2 θ + cos2 θ = 1
2) sec2 θ -tan2 θ = 1
3) cosec2 θ - cot2 θ = 1
4) sin θ cosec θ = tan θ cot θ = sec θ cos θ = 1
5) sin2 θ + cos2 θ = 1, so each of them is numerically less than 1.
6) |sin θ| ≤ 1 and |cos θ| ≤ 1
7) -1 <cosec θ<1 and -1 <sec θ<1
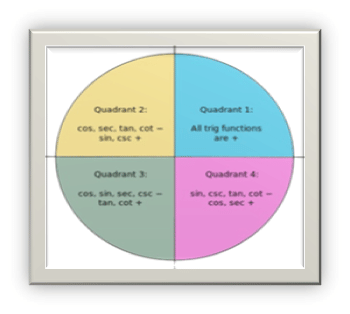
8) tan θ and cot θ may take any value. - The trigonometry ratios can be either positive or negative depending on the quadrant in which they lie. The figure given below illustrates the various trigonometric ratios and their signs in various quadrants:
- Range of f: X →Y is the set of all images f(x) which belongs to Y, i.e.
Range f = {f(x) ∈ Y: x ∈ X} ⊆ Y.
The domain and range of various trigonometry ratios are given below:Trigonometric FunctionDomainRangesin xR-1 ≤ sin x ≤1cos xR-1 ≤ cos x ≤1tan xR – {(2n + 1)π/2, n ∈ I}Rcosec xR – {nπ, n ∈ I}R – {x: -1 < x <1}sec xR – {(2n + 1)π/2, n ∈ I}R – {x: -1 < x <1}cot xR – {nπ, n ∈ I}R - Given below is the trigonometry table of the basic ratios for some frequently used angles. These formulas must be memorized as they are used in almost all questions:Angle (x)sin xcos xtan xcosec xsec xcot x0°010undefined1undefined90° = π/210undefined1undefined0180° = π0-10undefined-1undefined270° =3π/2-10undefined-1undefined0360° = 2π010undefined1undefined
- Some other formulas of trigonometry which are useful in solving questions:Angles0°30°45°60°90°sin01/21/√2√3/21cos1√3/21/√21/20tan0√3/21√3undefinedcosecundefined2√22/√31sec12/√3√22undefinedcotundefined√311/√30
- The values of various trigonometric ratios vary in different quadrants. The variation is listed below quadrant wise:1. sine- increases from 0 to 1First Quadrant
2. cosine- decreases from 1 to 0
3. tangent- increases from 0 to ∞
4. cotangent- decreases from ∞ to 0
5. secant- increases from 1 to ∞
6. cosecant- decreases from ∞ to 11. sine- decreases from 1 to 0Second Quadrant
2. cosine- decreases from 0 to -1
3. tangent- increases from -∞ to 0
4. cotangent- decreases from 0 to -∞
5. secant- increases from -∞ to -1
6. cosecant- increases from 1 to ∞1. sine- decreases from 0 to -1Third Quadrant
2. cosine- increases from -1 to 0
3. tangent- increases from 0 to ∞
4. cotangent- decreases from ∞ to 0
5. secant- decreases from -1 to -∞
6. cosecant- increases from -∞ to -11. sine- increases from -1 to 0Fourth Quadrant
2. cosine- increases from 0 to 1
3. tangent- increases from -∞ to 0
4. cotangent- decreases from 0 to -∞
5. secant- decreases from ∞ to 1
6. cosecant- decreases from -1 to ∞- Sin and cos both have 2π as their period.
- tan function has π as the period.
- The reciprocal functions have the same period as that of the original functions.
- If the period of f(x) is T then that of kf(ax+b) is T/mod (a), hence period is affected by coefficient of x only.
- If f(x) has its period T and g(x) has its period M, then (af(x) + bg(x)) has its period < L.C.M. (T, M). Moreover if f(x) and g(x) are basic trigonometric functions then period of [af (x) + bg(x)] = L.C.M. (T, M).
- If a constant is added, subtracted, multiplied or divided in a periodic function, its period is unaffected.
- Graphs of some basic trigonometric functions:
1) sin x
2) cos x 
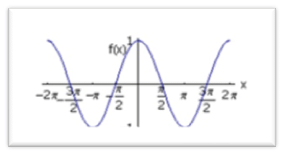3) tan x 
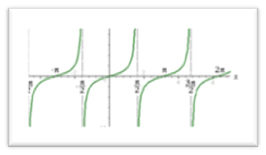4) cot x 
5) sec x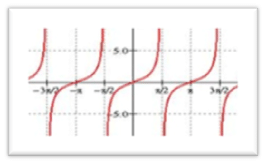 
The document Trigonometric Functions Class 11 Notes Maths Chapter 3 is a part of the JEE Course Mock Tests for JEE Main and Advanced 2025.
All you need of JEE at this link: JEE
|
357 docs|100 tests
|
FAQs on Trigonometric Functions Class 11 Notes Maths Chapter 3
| 1. What are the basic trigonometric functions? |  |
| 2. How are the trigonometric functions defined on the unit circle? | |
Ans. On the unit circle, the trigonometric functions are defined as follows: the sine of an angle is the y-coordinate of the point on the unit circle corresponding to that angle, the cosine of an angle is the x-coordinate, and the tangent of an angle is the ratio of the sine to the cosine.
| 3. What is the range of the sine and cosine functions? | |
Ans. The range of the sine and cosine functions is [-1, 1]. This means that the values of these functions can never exceed 1 or be less than -1.
| 4. How are the reciprocal trigonometric functions defined? | |
Ans. The reciprocal trigonometric functions are the cosecant (csc), secant (sec), and cotangent (cot). They are defined as the reciprocals of the sine, cosine, and tangent functions, respectively. For example, the cosecant of an angle is equal to 1 divided by the sine of that angle.
| 5. What are the periodicity and symmetry properties of the trigonometric functions? | |
Ans. The sine and cosine functions are periodic with a period of 2π. This means that their values repeat every 2π radians or 360 degrees. The tangent function is also periodic, but with a period of π. The sine function is an odd function, which means that sin(-x) = -sin(x), while the cosine function is an even function, which means that cos(-x) = cos(x).
Related Exams
About this Document
4.64/5
Rating
Apr 18, 2025
Last updated
Document Description: Revision Notes - Trigonometric Functions for JEE 2025 is part of Mock Tests for JEE Main and Advanced 2025 preparation.
The notes and questions for Revision Notes - Trigonometric Functions have been prepared according to the JEE exam syllabus. Information about Revision Notes - Trigonometric Functions covers topics
like and Revision Notes - Trigonometric Functions Example, for JEE 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Revision Notes - Trigonometric Functions.
Introduction of Revision Notes - Trigonometric Functions in English is available as part of our Mock Tests for JEE Main and Advanced 2025
for JEE & Revision Notes - Trigonometric Functions in Hindi for Mock Tests for JEE Main and Advanced 2025 course.
Download more important topics related with notes, lectures and mock test series for JEE
Exam by signing up for free. JEE: Trigonometric Functions Class 11 Notes Maths Chapter 3
Description
Full syllabus notes, lecture & questions for Trigonometric Functions Class 11 Notes Maths Chapter 3 - JEE | Plus excerises question with solution to help you revise complete syllabus for Mock Tests for JEE Main and Advanced 2025 | Best notes, free PDF download
Information about Revision Notes - Trigonometric Functions
In this doc you can find the meaning of Revision Notes - Trigonometric Functions defined & explained in the simplest way possible. Besides explaining types of
Revision Notes - Trigonometric Functions theory, EduRev gives you an ample number of questions to practice Revision Notes - Trigonometric Functions tests, examples and also practice JEE
tests
Related Searches
Summary
,Extra Questions
,Sample Paper
,past year papers
,practice quizzes
,video lectures
,Viva Questions
,Trigonometric Functions Class 11 Notes Maths Chapter 3
,mock tests for examination
,study material
,shortcuts and tricks
,Trigonometric Functions Class 11 Notes Maths Chapter 3
,ppt
,MCQs
,Free
,Trigonometric Functions Class 11 Notes Maths Chapter 3
,Exam
,Previous Year Questions with Solutions
,Semester Notes
,Objective type Questions
,Important questions
;
Additional Information about Revision Notes - Trigonometric Functions for JEE Preparation
Revision Notes - Trigonometric Functions Free PDF Download
The Revision Notes - Trigonometric Functions is an invaluable resource that delves deep into the core of the JEE exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Revision Notes - Trigonometric Functions now and kickstart your journey towards success in the JEE exam.
Importance of Revision Notes - Trigonometric Functions
The importance of Revision Notes - Trigonometric Functions cannot be overstated, especially for JEE aspirants.
This document holds the key to success in the JEE exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Revision Notes - Trigonometric Functions
Revision Notes - Trigonometric Functions Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Revision Notes - Trigonometric Functions.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Revision Notes - Trigonometric Functions Notes on EduRev are your ultimate resource for success.
Revision Notes - Trigonometric Functions JEE Questions
The "Revision Notes - Trigonometric Functions JEE Questions" guide is a valuable resource for all aspiring students preparing for the
JEE exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Revision Notes - Trigonometric Functions on the App
Students of JEE can study Revision Notes - Trigonometric Functions alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Revision Notes - Trigonometric Functions,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Revision Notes - Trigonometric Functions is prepared as per the latest JEE syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup