JEE Exam > JEE Notes > Mock Tests for JEE Main and Advanced 2026 > Revision Notes - Parabola
Parabola Class 11 Notes Maths Chapter 11
- The general equation of a conic is ax2 + 2hxy + by2 + 2gx + 2fy +c =0. Here if e =1 and D≠ 0, then it represents a parabola.
- The general equation of parabola is (y-y0)2 = (x-x0), which has its vertex at (x0, y0).
- The general equation of parabola with vertex at (0, 0) is given by y2 = 4ax, and it opens rightwards.
- The parabola x2 = 4ay opens upwards.
- The equation y2 = 4ax is considered to be the standard equation of the parabola for which the various components are
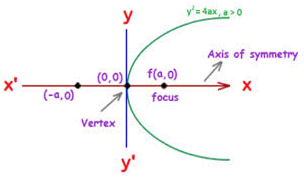1. Vertex at (0,0)
2. Directrix is x+a = 0
3. Axis is y = 0
4. Focus is (a, 0)
5. Length of latus rectum = 4a
6. Ends of latus rectum are L(a, 2a) and L’(a, -2a) - The parabola y = a(x – h)2 + khas its vertex at (h, k)
- The perpendicular distance from focus on directrix is half the length of latus rectum
- Vertex is the middle point of the focus and the point of intersection of directrix and axis
- Two parabolas are said to be equal if they have the same latus rectum
- The point (x1, y1) lies outside, on or inside the parabola y2 = 4ax, according as the expression y12 = 4ax1 is positive, zero or negative.
- Length of the chord intercepted by the parabola on the line y = mx + c is (4/m2) √a(1+m2) (a-mc)
- Length of the focal chord which makes an angle δ with the x-axis is 4a cosec2δ
- In parametric form, the parabola is represented by the equations x = at2 and y =2at
- The equation of a chord joining t1 and t2 is given by 2x – (t1 + t2) y + 2at1t2 = 0
- If a chord joining t1, t2 and t3, t4 pass through a point (c, 0) on the axis, then t1t2 = t3t4 = -c/a
- Tangents to the parabola y2 = 4ax
1. yy1 = 2a(x+x1) at the point (x1, y1)
2. y = mx + a/m ( m ≠ 0) at (a/m2, 2a/m)
3. ty = x+at2 at (at2, 2at) - Normals to the parabola y2 = 4ax
1. y-y1 = -y1/ 2a(x-x1) at the point (x1, y1)
2. y = mx -2am – am3 at (am2, -2am)
3. y + tx = 2at +at3 at (at2, 2at) - The equation of the director circle to the parabola is x + a = 0 which is same as the equation of the directrix
- The circle circumscribing the triangle formed by any three tangents to a parabola passes through the focus.
- The orthocenter of any triangle formed by three tangents to a parabola y2 = 4ax lies on then directrix and has the coordinates –a, a(t1 + t2 + t3 + t1t2t3).
- The area of the triangle formed by three points on a parabola is twice the area of the triangle formed by the tangents at these points.
- A circle circumscribing the triangle formed by three co-normal points passes through the vertex of the parabola and its equation is given by 2(x2 + y2)– 2(h+2a)x - ky =0
The two vital parabolas along with their basic components like vertex and directrix are tabulated below:
The document Parabola Class 11 Notes Maths Chapter 11 is a part of the JEE Course Mock Tests for JEE Main and Advanced 2026.
All you need of JEE at this link: JEE
|
517 docs|120 tests
|
FAQs on Parabola Class 11 Notes Maths Chapter 11
| 1. What is a parabola? |  |
Ans. A parabola is a U-shaped curve that is formed by the graph of a quadratic equation. It is symmetric about a line called the axis of symmetry and has a vertex, which is the lowest or highest point on the curve.
| 2. How do you identify the equation of a parabola? | |
Ans. To identify the equation of a parabola, you need to know its vertex and whether it opens upwards or downwards. If the vertex is at the point (h, k) and the parabola opens upwards, the equation can be written as y = a(x - h)^2 + k. If it opens downwards, the equation would be y = -a(x - h)^2 + k, where 'a' is a constant.
| 3. How can you find the vertex of a parabola? | |
Ans. The vertex of a parabola can be found using the formula (-b/2a, f(-b/2a)), where 'a' and 'b' are the coefficients of the quadratic equation in the form ax^2 + bx + c = 0. By substituting this value of 'x' into the equation, you can find the corresponding 'y' coordinate of the vertex.
| 4. How can you determine if a parabola opens upwards or downwards? | |
Ans. The coefficient 'a' in the quadratic equation determines whether a parabola opens upwards or downwards. If 'a' is positive, the parabola opens upwards, and if 'a' is negative, the parabola opens downwards.
| 5. Can a parabola intersect the x-axis at more than two points? | |
Ans. No, a parabola can intersect the x-axis at a maximum of two points. This is because a quadratic equation can have a maximum of two real roots. If the discriminant of the quadratic equation is greater than zero, it will intersect the x-axis at two distinct points. If the discriminant is zero, it will intersect the x-axis at a single point, which is the vertex of the parabola. If the discriminant is negative, the parabola will not intersect the x-axis.
About this Document
4.92/5
Rating
Sep 28, 2025
Last updated
Related Exams
Document Description: Revision Notes - Parabola for JEE 2025 is part of Mock Tests for JEE Main and Advanced 2026 preparation.
The notes and questions for Revision Notes - Parabola have been prepared according to the JEE exam syllabus. Information about Revision Notes - Parabola covers topics
like and Revision Notes - Parabola Example, for JEE 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Revision Notes - Parabola.
Introduction of Revision Notes - Parabola in English is available as part of our Mock Tests for JEE Main and Advanced 2026
for JEE & Revision Notes - Parabola in Hindi for Mock Tests for JEE Main and Advanced 2026 course.
Download more important topics related with notes, lectures and mock test series for JEE
Exam by signing up for free. JEE: Parabola Class 11 Notes Maths Chapter 11
Description
Full syllabus notes, lecture & questions for Parabola Class 11 Notes Maths Chapter 11 - JEE | Plus excerises question with solution to help you revise complete syllabus for Mock Tests for JEE Main and Advanced 2026 | Best notes, free PDF download
Information about Revision Notes - Parabola
In this doc you can find the meaning of Revision Notes - Parabola defined & explained in the simplest way possible. Besides explaining types of
Revision Notes - Parabola theory, EduRev gives you an ample number of questions to practice Revision Notes - Parabola tests, examples and also practice JEE
tests
Related Searches
Objective type Questions
,study material
,Exam
,practice quizzes
,mock tests for examination
,Summary
,video lectures
,Extra Questions
,Free
,shortcuts and tricks
,Parabola Class 11 Notes Maths Chapter 11
,Previous Year Questions with Solutions
,Important questions
,ppt
,Viva Questions
,Semester Notes
,Parabola Class 11 Notes Maths Chapter 11
,MCQs
,Parabola Class 11 Notes Maths Chapter 11
,Sample Paper
,past year papers
;
Additional Information about Revision Notes - Parabola for JEE Preparation
Revision Notes - Parabola Free PDF Download
The Revision Notes - Parabola is an invaluable resource that delves deep into the core of the JEE exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Revision Notes - Parabola now and kickstart your journey towards success in the JEE exam.
Importance of Revision Notes - Parabola
The importance of Revision Notes - Parabola cannot be overstated, especially for JEE aspirants.
This document holds the key to success in the JEE exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Revision Notes - Parabola
Revision Notes - Parabola Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Revision Notes - Parabola.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Revision Notes - Parabola Notes on EduRev are your ultimate resource for success.
Revision Notes - Parabola JEE Questions
The "Revision Notes - Parabola JEE Questions" guide is a valuable resource for all aspiring students preparing for the
JEE exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Revision Notes - Parabola on the App
Students of JEE can study Revision Notes - Parabola alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Revision Notes - Parabola,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Revision Notes - Parabola is prepared as per the latest JEE syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up
within 7 days!
within 7 days!
Takes less than 10 seconds to signup