JEE Advanced (Subjective Type Questions): Permutations & Combinations | Chapter-wise Tests for JEE Main & Advanced PDF Download
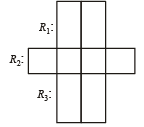
1. Six X's have to be placed in the squares of figure below in such a way that each row contains at least one X. In how many different ways can this be done. (1978)

Ans. Sol. As all the X’s are identical, the question is of selection of 6 squares from 8 squares, so that no row remains empty. Here R1 has 2 squares, R2 has 4 squares and R3 has 2 squares.
The selection scheme is as follows :
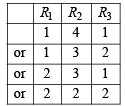
∴ Number of selections are
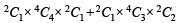
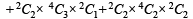
Q.2. Five balls of different colours are to be placed in there boxes of different size. Each box can hold all five. In how many different ways can we place the balls so that no box remains empty ?
Ans.
Sol. The various possibilities to put 5 different balls in 3 different size boxes, when no box remains empty : The balls can be 1, 1 and 3 in different boxes or 2, 2, 1.
Case I : To put 1, 1 and 3 balls in different boxes. Selection of 1, 1 and 3 balls out of 5 balls can be done in 5C1 × 4C1 × 3C3 ways and then 1, 1, 3 can permute (as defferent size boxes) in 3! ways.
∴ No. of ways = 5C1 × 4C1 × 3C3× 3! = 5 × 4× 1 × 6 = 120
Case II : To put 2, 2 and 1 ball in different boxes. Selection of 2, 2 and 1 balls out of 5 balls can be done in 5C2 × 3C2 × 1C1 ways and then 2, 2, 1 can permute (different boxes) in 3! ways
∴ No. of ways = 5C1 × 3C2 × 1C1× 3! = 10 × 3 × 1 × 6 = 180
Combining case I and II, total number of required ways are = 120 + 180 = 300.
Q.3. m men and n women are to be seated in a row so that no two women sit together. If m > n, then show that the number of ways in which they can be seated is
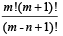 (1983 - 2 Marks)
(1983 - 2 Marks)
Ans.
Sol. m men can be seated in m! ways creating (m +1) places for ladies to sit. n ladies out of (m + 1) places (as n < m) can be seated in m + 1Pn ways
∴ Total ways = m! × m + 1Pn
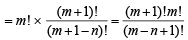
Q.4. 7 relatives of a man comprises 4 ladies and 3 gentlemen; his wife has also 7 relatives; 3 of them are ladies and 4 gentlemen. In how many ways can they invite a dinner party of 3 ladies and 3 gentlemen so that there are 3 of man’s relatives and 3 of the wife’s relatives? (1985 - 5 Marks)
Ans.
Sol. There are four possibilities:
(i) 3 ladies from husband’s side and 3 gentlemen from wife’s side.
No. of ways in this case = 4C3 × 4C3 = 4 × 4 = 16
(ii) 3 gentlemen from husband’s side and 3 ladies from wife’s side.
No. of ways in this case= 3C3 × 3C3 = 1 × 1 = 1
(iii) 2 ladies and one gentlemen from husband’s side and one lady and 2 gentlemen from wife’s side.
No. of ways in this case = (4C2 × 3C1 ) × (3C1 × 4C2) = 6 × 3 × 3× 6 = 324
(iv) One lady and 2 gentlemen from husband’s side and 2 ladies and one gentlemen from wife’s side.
No. of ways in this case = (4C1 × 3C2 ) × (3C2 × 4C1 ) = 4 × 3 × 3× 4 = 144
Hence the total no. of ways are = 16 + 1 + 324 + 144 = 485
Q.5. A box contains two white balls, three black balls and four red balls. In how many ways can three balls be drawn from the box if at least one black ball is to be included in the draw? (1986 - 2½ Marks)
Ans.
Sol. Number of ways of drawing at least one black ball
= 1 black and 2 other or 2 black and 1 other or 3 black
= 3C1 × 6C2 + 3C2 × 6C1 + 3C3
= 3 × 15 + 3 × 6+1
= 45 + 18 + 1 = 64
Q.6. Eighteen guests have to be seated, half on each side of a long table. Four particular guests desire to sit on one particular side and three others on the other side. Determine the number of ways in which the sitting arrangements can be made. (1991 - 4 Marks)
Ans.
Sol. Out of 18 guests half i.e. 9 to be seated on side A and rest 9 on side B. Now out of 18 guests, 4 particular guests desire to sit on one particular side say side A and other 3 on other side B. Out of rest 18 – 4 – 3 = 11 guests we can select 5 more for side A and rest 6 can be seated on side B. Selection of 5 out of 11 can be done in 11C5 ways and 9 guests on each sides of table can be seated in 9! × 9! ways. Thus there are total 11C5 × 9! × 9! arrangements.
Q.7. A committee of 12 is to be formed from 9 women and 8 men.
In how many ways this can be done if at least five women have to be included in a committee? In how many of these committees (1994 - 4 Marks) (a) The women are in majority? (b) The men are in majority?
Ans.
Sol. Given that there are 9 women and 8 men. A committee of 12 is to be formed including at least 5 women.
This can be doen in the following ways.
=5W and 7M or 6W and 6M
or 7W and 5M
or 8W and 4M
or 9W and 3M
No. of ways of forming committee is
= 9C5 × 8C7 + 9C6 × 8C6 + 9C7 × 8C5 + 9C8 × 8C4 + 9C9 × 8C3
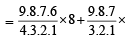
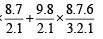
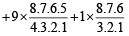
= 126 × 8 + 84 × 28 + 36 × 56 + 9× 70 + 56 = 6062 ways.
(a) The women are in majority in 2016 + 630 + 56 = 2702 ways.
(b) The men are in majority in 1008 ways.
Q.8. Prove by permutation or oth erwise 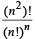 is an integer (n ∈ I+). (2004 - 2 Marks)
is an integer (n ∈ I+). (2004 - 2 Marks)
Ans.
Sol. Let there be n sets of different objects each set containing n identical objects [eg (1, 1, 1 ... 1 (n times) ), (2, 2, 2 ..., 2
(n times) ... (n, n, n ... n (n times))]
Then the no. of ways in which these n × n = n2 objects can be arranged in a row =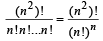
But these number of ways should be a natural number.
Hence 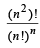 is an integer. (n ∈ I+)
is an integer. (n ∈ I+)
Q.9. If total number of runs scored in n matches is
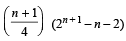 where n > 1, and the runs scored in the kth match are given by k. 2n + 1– k, where 1 ≤ k ≤ n. Find n. (2005 - 2 Marks)
where n > 1, and the runs scored in the kth match are given by k. 2n + 1– k, where 1 ≤ k ≤ n. Find n. (2005 - 2 Marks)
Ans. Sol. Given that runs scored in kth match 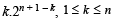
and runs scored in n matches =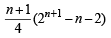
∴ 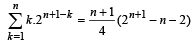
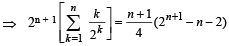
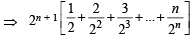
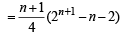 ....(i)
....(i)
Let 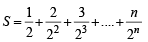
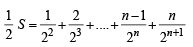
Subtracting the above two, we get
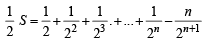
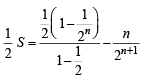 ⇒
⇒ 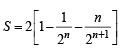
∴ Equation (i) becomes
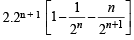
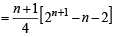
⇒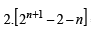
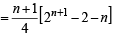
⇒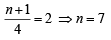
|
446 docs|930 tests
|
















