JEE Advanced (Fill in the Blanks): Sequences & Series | Chapter-wise Tests for JEE Main & Advanced PDF Download
Q.1. The sum of integers from 1 to 100 that are divisible by 2 or 5 is .............. (1984 - 2 Marks)
Ans. 3050
Sol. The sum of integers from 1 to 100 that are divisible by 2 or = sum of integers from 1 to 100 divisible by 2 + sum of integers from 1 to 100 divisible by 5 – sum of integers from 1 to 100 divisible by 10
= (2 + 4 + 6 +...+ 100) + (5 + 10 + 15 +...+ 100)
– (10 + 20 +...+ 100)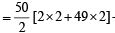
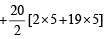
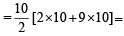
= 2550 + 1050 – 550 = 3050
Q.2. The solution of the equation 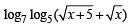 is .............. (1986 - 2 Marks)
is .............. (1986 - 2 Marks)
Ans. 4
Sol. The given equation is
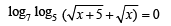
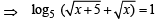
Squaring both sides

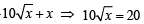
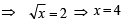
Q.3. The sum of the first n terms of the series
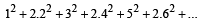 ....... is
....... is
n (n + 1) 2/2, when n is even. When n is odd, the sum is .............. (1988 - 2 Marks)
Ans.
Sol. When n is odd, let n = 2m + 1
∴ The req. sum
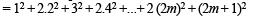
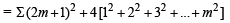
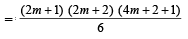
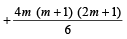
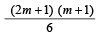 [2 (4m + 3) + 4m]
[2 (4m + 3) + 4m]
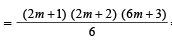
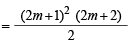
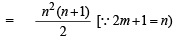
Q.4. Let the harmonic mean and geometric mean of two positive numbers be the ratio 4 : 5. Then the two number are in the ratio .............. (1992 - 2 Marks)
Ans. 4 : 1 or 1 : 4
Sol. Let a and b be two positive numbers.
Then, H.M. 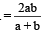 and G.M.
and G.M. 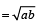
ATQ HM : GM = 4 : 5
∴ 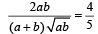
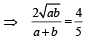
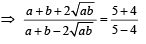
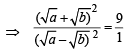

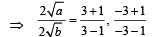
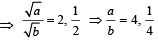
a : b = 4 : 1 or 1 : 4
Q.5. For any odd integer n ≥ 1, n3-(n-1)3+...+(-1)n-1 13 = .............. (1996 - 1 Mark)
Ans.
Sol. Since n is an odd integer, (– 1)n–1 = 1 and n – 1, n – 3, n – 5, .... are even integers.
We have
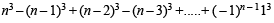
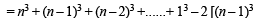
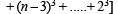
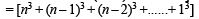
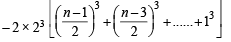
[∴ n – 1, n – 3.........are even integers] Here the first square bracket contain the sum of cubes of 1st n natural numbers. Whereas the second square bracket contains the sum of the cubes of natural numbers from 1 to
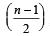 , where n – 1, n – 3, ...... are even integers. Using the formula for sum of cubes of 1st n natural numbers we get the summation
, where n – 1, n – 3, ...... are even integers. Using the formula for sum of cubes of 1st n natural numbers we get the summation
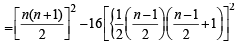
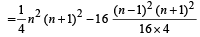
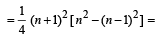
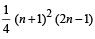
Q.6. Let p and q be roots of the equation x2 – 2x + A = 0 and let r and s be the roots of the equation x2 – 18x + B = 0. If p < q < r < s are in arithmetic progression, then A = .............. and B = .............. (1997 - 2 Marks)
Ans. –3, 77
Sol. It is given p + q = 2, pq = A and r + s = 18, rs = B and it is given that p,q, r, are in A.P.
Therefore, let p = a – 3s, q = a – d, r = a + d and s = a + 3d.
As p < q < r < s, we have d > 0
Now, 2 = p + q = a – 3d + a – d = 2a – 4d
⇒ a – 2d = 1 ....(1)
Again 18 = r + s = a + d + a + 3d
⇒ 18 = 2a + 4d ⇒ 9 = a + 2d. ....(2)
Subtracting (1) from (2) ⇒ 8 = 4d ⇒ 2 = d
Putting in (2) we obtain a = 5
∴ p = a – 3d = 5 – 6 = – 1,
q = a – d = 5 – 2 = 3 r = a + d = 5 + 2 = 7,
s = a + 3d = 5 + 6 = 11
Therefore, A = pq = – 3 and B = rs = 77.
|
481 docs|964 tests
|
















