JEE Advanced (Matrix Match): Inverse Trigonometric Functions | Chapter-wise Tests for JEE Main & Advanced PDF Download
DIRECTIONS (Q. 1 & 2) : Each question contains statements given in two columns, which have to be matched. The statements in Column-I are labelled A, B, C and D, while the statements in Column-II are labelled p, q, r, s and t. Any given statement in Column-I can have correct matching with ONE OR MORE statement(s) in Column-II. The appropriate bubbles corresponding to the answers to these questions have to be darkened as illustrated in the following example :
If the correct matches are A-p, s and t; B-q and r; C-p and q; and D-s then the correct darkening of bubbles will look like the given.

Q. 1. Match the following
Column I Column II
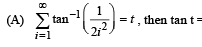 (p) 1
(p) 1
(B) Sides a, b, c of a triangle ABC are in AP and (q) 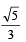
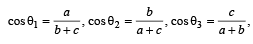
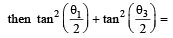
(C) A line is perpendicular to x + 2y + 2z = 0 and (r) 2/3
passes through (0, 1, 0). The perpendicular
distance of this line from the origin is
Ans. (A)-(p), (B)-(r), (C)-(q)
Solution.
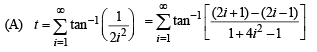
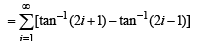
t = tan–1 3 – tan–1 1 + tan–15 – tan–13 + ...... + tan–1(2n + 1) – tan–1 (2n – 1) + ...... ∞
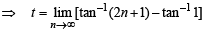
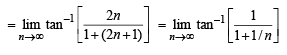
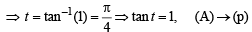
(B) ∴ a, b, c are in AP ⇒ 2b = a + c
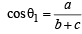
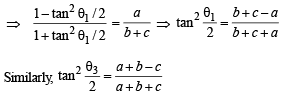
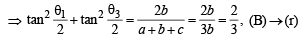
(C) Equation of line through (0, 1, 0) and perpendicular to
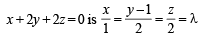
For some value of λ, the foot of perpendicular from origin to line is (λ, 2λ + 1, 2λ)
Dr ’s of this ^ from origin are λ , 2λ + 1, 2λ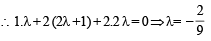
∴ Foot of perpendicular is 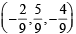
∴ Required distance
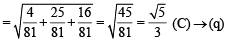
Q. 2. Let (x, y) be such that 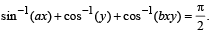
Match the statements in Column I with statements in Column II and indicate your answer by darkening the appropriate bubbles in the 4 × 4 matrix given in the ORS.
Column I Column II
(A) If a = 1 and b = 0, then (x, y) (p) lies on the circle x2 + y2 = 1
(B) If a = 1 and b = 1, they (x, y) (q) lies on (x2 – 1)(y2 – 1) = 0
(C) If a = 1 and b = 2, then (x, y) (r) lies on y = x
(D) If a = 2 and b = 2, then (x, y) (s) lies on (4x2 – 1) (y2 – 1) = 0
Ans. (A) → p, (B) → q, (C) → p , (D) → s
Solution.
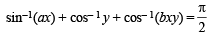
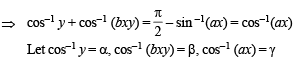
⇒ y = cos α, bxy = cos β, αx = cos γ
∴ We get α + β = γ and cos β = bxy
⇒ cos (γ – α) = bxy
⇒ cos y cos α + sin γ sin α = bxy
⇒ axy + sin γ sin α = bxy ⇒ (a – b) xy = – sin α sin γ
⇒ (a – b)2 x2y2 = – sin2 α sin2 γ
= (1– cos2 α) (1– cos2 γ)
⇒ (a – b)2 x2y2 = (1– a2x2) (1– y2) ....(1)
(A) For a = 1, b = 0, equation (1) reduces to
x2y2 = (1 – x2) (1– y2) ⇒ x2 + y2 = 1
(B) For a = 1, b = 1 equation (1) becomes
(1– x2) (1– y2) = 0 ⇒ (x2 – 1) (y2 – 1) = 0
(C) For a = 1, b = 2 equation (1) reduces to
x2y2 = (1– x2) (1– y2) ⇒ x2 + y2 = 1
(D) For a = 2, b = 2 equation (1) reduces to
0 = (1– 4x2) (1– y2) ⇒ (4x2 – 1) (y2 – 1) = 0
DIRECTIONS (Q. 3) : Following question has matching lists. The codes for the lists have choices (a), (b), (c) and (d) out of which ONLY ONE is correct.
Q. 3. Match List I with List II and select the correct answer using the code given below the lists :
List I List II
P.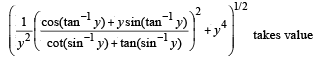 1.
1. 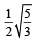
Q. If cosx + cosy + cosz = 0 = sinx + siny + sinz then possible value of cos 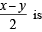 2. √2
2. √2
R. 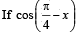 cos 2x + sinx sin 2 secx = cosx sin2x secx + 3. 1/2
cos 2x + sinx sin 2 secx = cosx sin2x secx + 3. 1/2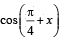 cos 2x then possible value of secx is
cos 2x then possible value of secx is
S. 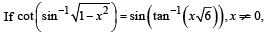 4. 1
4. 1
then possible value of x is
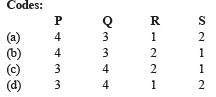
Ans. (b)
Solution.
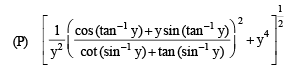
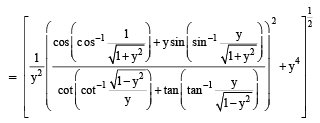
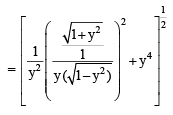
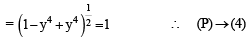
(Q) We have cos x + cos y = – cos z
sin x + sin y = – sin z
Squaring and adding we get
(cos x + cos y)2 + (sin x + sin y)2 = cos2 z + sin2 z
⇒ 2 + 2 cos (x – y) = 1
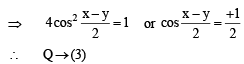
(R) We have
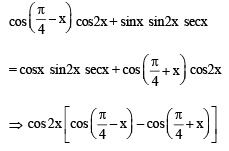
= sin2x secx (cosx – sinx)
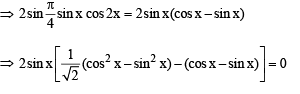
∴ (R) → (2)
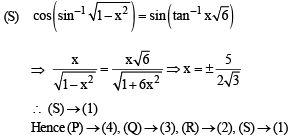
|
446 docs|929 tests
|
















