Integer Answer Type Questions: Matrices and Determinants | JEE Advanced | 35 Years Chapter wise Previous Year Solved Papers for JEE PDF Download
Q. 1. Let w be the complex number 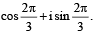 Then the number of distinct complex numbers z satisfying
Then the number of distinct complex numbers z satisfying 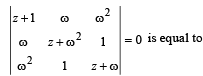
Ans. 0
Solution.
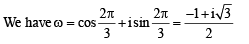
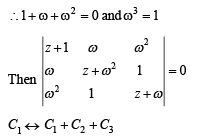
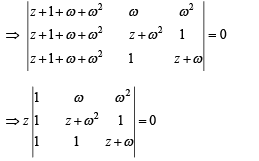
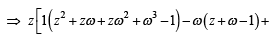
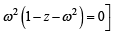
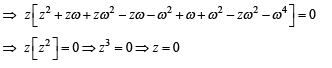
∴ z = 0 is the only solution.
Q. 2. Let k be a positive r eal n umber and let 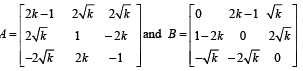
If det (adj A) + det (adj B) = 106. then [k] is equal to
[Note : adj M denotes the adjoint of square matrix M and [k] denotes the largest integer less than or equal k.
Ans. 4
Solution.
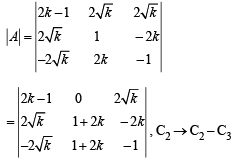

= (1 + 2k) (8k – 4k + 4k2+ 1) = (2k+ 1)3
Also B = 0 as B is skew symmetric of odd order..
∴ |Adj A| + |Adj B| = |A|2 + |B|2 = 106
⇒ (2k + 1)6 = 106 ⇒ 2k + 1 = 10 ⇒ k= 4.5
∴ [k] = 4
Q. 3. Let M be a 3 × 3 matrix satisfying 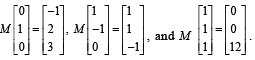 Then the sum of the diagonal entries of M is
Then the sum of the diagonal entries of M is
Ans. 9
Solution.
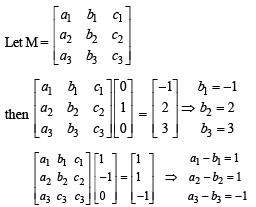
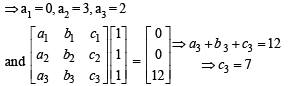
∴ Sum of diagonal elements = a1 + b2 + c3 = 0 + 2 + 7 = 9
Q. 4. The total number of distinc 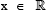 for which
for which 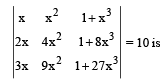
Ans. 2
Solution.

Operating C2 – C1, C3 – C1 for both the determinants, we get
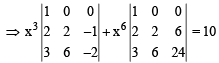
⇒ x3 (–4 + 6) + x6 (48 – 36) = 10
⇒ 2x3 + 12x6 = 10 ⇒ 6x6 + x3 – 5 = 0
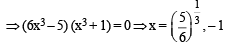
Q. 5. 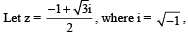 and r, s ∈ {1, 2, 3}. Let
and r, s ∈ {1, 2, 3}. Let 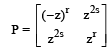 and I be the identity matrix of order 2. Then the total number of ordered pairs (r, s) for which P2 = –I is
and I be the identity matrix of order 2. Then the total number of ordered pairs (r, s) for which P2 = –I is
Ans. 1
Solution.
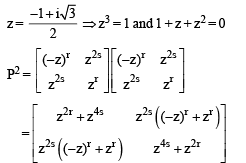
For P2 = – I we should have z2r + z4s = – 1 and z2s ((–z)r + zr) = 0
⇒ z2r + zs + 1 = 0 and (–z)r + zr = 0
⇒ r is odd and s = r but not a multiple of 3.
Which is possible when s = r = 1
∴ only one pair is there.
|
347 docs|185 tests
|
FAQs on Integer Answer Type Questions: Matrices and Determinants - JEE Advanced - 35 Years Chapter wise Previous Year Solved Papers for JEE
| 1. What is the difference between a matrix and a determinant? |  |
| 2. How do you find the determinant of a matrix? |  |
| 3. What does a zero determinant of a matrix indicate? |  |
| 4. Can a matrix have a negative determinant? |  |
| 5. What is the significance of the determinant in linear algebra? |  |
















