JEE Advanced (Subjective Type Questions): Circle | Chapter-wise Tests for JEE Main & Advanced PDF Download
Q.1. Find the equation of the circle whose radius is 5 and which touches the circle x2 + y2 – 2x – 4y – 20 = 0 at the point (5, 5). (1978)
Ans. x2 + y2 – 18x – 16y + 120 = 0
Sol. The given circle is
x2 + y2 – 2x – 4y – 20 = 0 whose centre is (1, 2) and radius = 5 Radius of required circle is also 5.
Let its centre be C2 (α, β). Both the circles touch each other at P (5, 5).
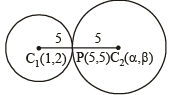
It is clear from figure that P (5, 5) is the mid-point of C1C2.
Therefore, we should have
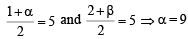 and β = 8
and β = 8
∴ Centre of requir ed cir cle is (9, 8) and equation of required circle is
(x – 9)2 + (y – 8)2 = 52
⇒ x2 + y2 – 18x – 16y + 120 = 0
Q.2. Let A be the centre of the circle x2 + y2 – 2x – 4y – 20 = 0.
Suppose that the tangents at the points B(1, 7) and D(4. –2) on the circle meet at the point C. Find the area of the quadrilateral ABCD. (1981 - 4 Marks)
Ans. 75 sq. units
Sol. The eq. of circle is
x2 + y2 – 2x – 4y – 20 = 0
Centre (1, 2), radius =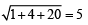
Using eq. of tangent at (x1, y1) of
x2 + y2 + 2gx1 + 2fy1 + c = 0 is
xx1 + yy1 + g (x + x1) f (y + y1) + c = 0
Eq. of tangent at (1, 7) is x . 1 + y . 7 – (x + 1) – 2 (y + 7) – 20 = 0
⇒ y – 7 = 0 … (1) Similarly eq. of tangent at (4, – 2) is

4x – 2y – (x + 4) –2 (y – 2) – 20 = 0
⇒ 3x – 4y – 20 = 0 … (2)
For pt C, solving (1) and (2),
we get x = 16, y = 7 ∴ C (16, 7).
Now, clearly ar (quad ABCD) = 2 Ar (rt ΔABC)
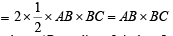
where AB = radius of circle = 5 and BC = length of tangent from C to circle

∴ ar (quad ABCD) = 5 × 15 = 75 sq. units.
Q.3. Find the equations of the circle passing through (–4, 3) and touching the lines x + y = 2 and x – y = 2. (1982 - 3 Marks)
Ans.
Sol. Given st. lines are x + y = 2
x – y = 2
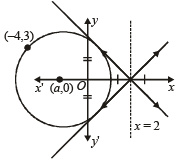
As centre lies on ∠ bisector of given equations (lines) which are the lines y = 0 and x = 2.
∴ Centre lies on x axis or x = 2.
But as it passes through (– 4, 3), i.e., II quadrant.
∴ Centre must lie on x-axis Let it be (a, 0) then distance between (a, 0) and (– 4, 3) is = length of ⊥ lar distance from (a, 0) to x + y – 2 = 0
⇒ (a + 4)2 + (0 – 3)2 = 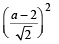
⇒ a2 + 20a + 46 = 0 ⇒ 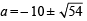
∴ Equation of circle is
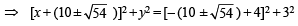
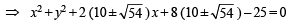
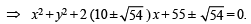
Q.4. Through a fixed point (h, k) secants are drawn to the circle x2 + y2 = r2. Show that the locus of the mid-points of the secants intercepted by the circle is x2 + y2 = hx + ky. (1983 - 5 Marks)
Ans. Sol. Equation of chord whose mid point is given is
T = S1
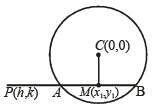
[Consider (x1, y1) be mid pt. of AB]
⇒ xx1 + yy1 – r2 = x12 + y12-r2
As it passes through (h, k),
∴ hx1 + ky1 = x12 +y12
∴ locus of (x1, y1) is, x2 + y2 = hx + ky
Q.5. The abscissa of the two points A and B are the roots of the equation x2 + 2ax – b2 = 0 and their ordinates are the roots of the equation x2 + 2px – q2 = 0. Find the equation and the radius of the circle with AB as diameter. (1984 - 4 Marks)
Ans.
Sol. Let the two points be A = (α1, β1) and B = (α2, β2)
Thus α1, α2 are roots of x2 + 2αx – b2 = 0
∴ α1 + α2 = – 2α … (1)
α1 α2 = – β2 … (2)
β1, β2 are roots of x2 + 2px – q2 = 0
∴ β1 + β2 = – 2p … (3)
β1β2 = – q2 … (4)
Now equation of circle with AB as diameter is (x – α1) (x – α2) + (y – β1) (y – β2) = 0
⇒ x2– (α1 + α2)x + α1α2 + y2– (β1 + β2)y + β1β2 = 0
⇒ x2 + 2αx – β2 + y2 + 2py – q2 = 0 [Using eq. (1), (2), (3) and (4)]
⇒ x2 + y2 + 2αx + 2py – b2 – q2 = 0
Which is the equation of required circle, with its centre (– a, – p) and radius 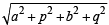
Q.6. Lines 5x + 12y – 10 = 0 and 5x – 12y – 40 = 0 touch a circle C1 of diameter 6. If the centre of C1 lies in the first quadrant, find the equation of the circle C2 which is concentric with C1 and cuts intercepts of length 8 on these lines. (1986 - 5 Marks)
Ans. Sol. Let equation of tangent PAB be 5x + 12y – 10 = 0 and that of
PXY be 5x – 12y – 40 = 0
Now let centre of circles C1 and C2 be C (h, k).
Let CM ⊥ PAB then CM = radius of C1 = 3
Also C2 makes an intercept of length 8 units on PAB ⇒ AM = 4
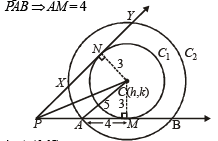
Then in ΔAMC, we get
∴ Radius of C2 is = 5 units
Also, as 5x + 12y – 10 = 0 … (1)
and 5x – 12y – 40 = 0 … (2)
are tangents to C1, length of perpendicular from C to AB = 3 units

⇒ 5h + 12k – 49 = 0 … (i)
or5h + 12k + 29 = 0 … (ii)
⇒ 5h – 12k – 79 = 0 … (iii)
or5h – 12k – 1 = 0 … (iv)
As C lies in first quadrant
∴ h, k are + ve
∴ Eq. (ii) is not possible.
Solving (i) and (iii), we get h = 64/5, k = – 5/4
This is also not possible.
Now solving (i) and (iv), we get h = 5, k = 2.
Thus centre for C2 is (5, 2) and radius 5.
Hence, equation of C2 is (x – 5)2 + (y – 2)2 = 52
⇒ x2 + y2 – 10x – 4y + 4 = 0
Q.7. Let a given line L1 intersects the x and y axes at P and Q, respectively. Let another line L2, perpendicular to L1, cut the x and y axes at R and S, respectively. Show that the locus of the point of intersection of the lines PS and QR is a circle passing through the origin. (1987 - 3 Marks)
Ans.
Sol. Let the equation of L1 be x cosα + y sin a = p1
Then any line perpendicular to L1 is x sin a – y cosα = p2, where p2 is a variable.
Then L1 meets x-axis at P (p1 secα, 0) and y-axis at Q (0, p1 cosecα).
Similarly L2 meets x-axis at R (p2 cosecα, 0) and y-axis at S (0, – p2 secα).
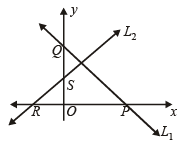
Now equation of PS is,
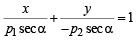
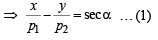
Similarly, equation of QR is,
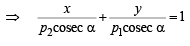
 … (2)
… (2)
Locus of point of intersection of PS and QR can be obtained by eliminating the variable p2 from (1) and (2)
i.e.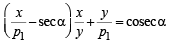
[Substituting the value of 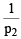 from (1) in (2)]
from (1) in (2)]
⇒ (x – p1 secα) x + y2 = p1y cosecα
⇒ x2 + y2 – p1 x secα – p1y cosecα = 0
which is a circle through origin.
Q.8. The circle x2 + y2 – 4x– 4y + 4 = 0 is inscribed in a triangle which has two of its sides along the co-ordinate axes. The locus of the circumcentre of the triangle is x + y – xy + k(x2 + y2)1/2 = 0. Find k. (1987 - 4 Marks)
Ans. Sol. The given circle is x2 + y2 – 4x – 4y + 4 = 0.
This can be re-written as (x – 2)2 + (y – 2)2 = 4
which has centre C (2, 2) and radius 2.
Let the eq. of third side AB of ΔOAB is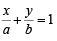 such that
such that
A (a, 0) and B (0, b)
Length of perpendicular form (2, 2) on AB = radius = CM = 2
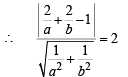
Since (2, 2) and origin lie on same side of AB
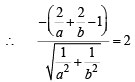
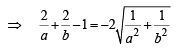 … (1)
… (1)
Since ∠AOB = π/2.
Hence, AB is the diameter of the circle passing through ΔOAB, mid point of AB is the centre of the circle i.e. (a/2, b/2)
Let centre be (h, k) 
then a = 2h, b = 2k.
Substituting the values of a and b in (1), we get
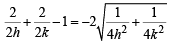
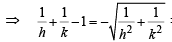
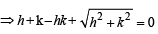
∴ Locus of M (h, k) is,
 … (2)
… (2)
Comparing it with given equation of locus of circumcentre of Δ i.e.
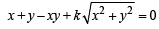 …(3)
…(3)
We get, k = 1
Q. 9. If 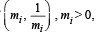 i = 1, 2, 3, 4 are four distinct points on a circle, then show that m1m2 m3m4 = 1 (1989 - 2 Marks)
i = 1, 2, 3, 4 are four distinct points on a circle, then show that m1m2 m3m4 = 1 (1989 - 2 Marks)
Ans. Sol. Given that 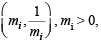 i = 1, 2, 3, 4 are four distinct points on a circle.
i = 1, 2, 3, 4 are four distinct points on a circle.
Let the equation of circle be x2 + y2 + 2gx + 2fy + c = 0
As the point 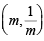 lies on it, therefore, we have
lies on it, therefore, we have
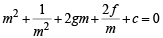
⇒ m4 + 2gm3 + cm2 + 2fm + 1 = 0
Since m1, m2, m3, m4 are roots of this equation, therefore product of roots = 1
⇒ m1m2m3m4 = 1
Q.10. A circle touches the line y = x at a point P such th at 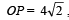 , where O is the origin. The circle contains the point (– 10, 2) in its interior and the length of its chord on the line x + y = 0 is
, where O is the origin. The circle contains the point (– 10, 2) in its interior and the length of its chord on the line x + y = 0 is 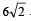 . Determine the equation of the circle. (1990 - 5 Marks)
. Determine the equation of the circle. (1990 - 5 Marks)
Ans. x2 + y2 + 18x – 2y + 32 = 0
Sol. Let AB be the length of ch ord intercepted by circle on y + x = 0
Let CM be perpendicular to AB from centre C (h, k).
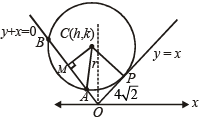
Also y – x = 0 and y + x = 0 are perpendicular to each other.
∴ OPCM is rectangle.
∴ CM = OP = 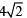
Let r be the radius of cirlce.
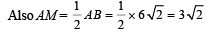
∴ In ΔCAM, AC2 = AM2 + MC2
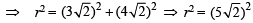
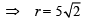
Again y = x is tangent to the circle at P
∴ CP = r
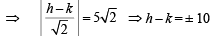 (1)
(1)
Also CM = 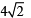
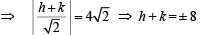 … (2)
… (2)
Solving four sets of eq’s given by (1) and (2), we get the possible centres as
(9, – 1), (1, – 9), (– 1, 9), (– 9, 1)
∴ Possible circles are (x – 9)2 + (y + 1)2 – 50
= 0 (x – 1)2 + (y + 9)2 – 50
= 0 (x + 1)2 + (y – 9)2 – 50
= 0 (x + 9)2 + (y – 1)2 – 50 = 0
But the pt (– 10, 2) lies inside the circle.
∴ S1 < 0
which is satisfied only for (x + 9)2 + (y – 1)2 – 50 = 0
∴ The required eq. of circle is x2 + y2 + 18x – 2y + 32 = 0
Q.11. Two circles, each of radius 5 units, touch each other at (1, 2).
If the equation of their common tangent is 4x + 3y = 10, find the equation of the circles. (1991 - 4 Marks)
Ans. Sol. Let t be the common tangent given by 4x + 3y = 10 … (1)
Common pt of contact being P (1, 2)
Let A and B be the centres of the circles, required.
Clearly, AB is the line perpendicular to t and passing through P (1, 2).
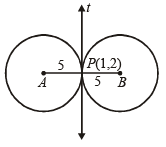
Therefore eq. of AB is
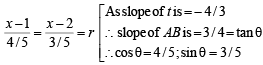
For pt A, r = – 5 and for pt B, r = 5, we get
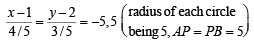
⇒ For pt A x = – 4 + 1, y = – 3 + 2
and For pt B x = 4 + 1, y = 3 + 2
∴ A (– 3, – 1) B (5, 5).
∴ Eq.’s of required circles are (x + 3)2 + (y + 1)2 = 52
and (x – 5)2 + (y – 5)2 = 52
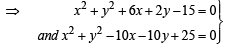
Q.12. Let a circle be given by 2x(x – a) + y(2y – b) = 0, (a ≠ 0, b ≠ 0).
Find the condition on a and b if two chords, each bisected by the x- axis, can be drawn to the circle from 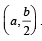 (1992 - 6 Marks)
(1992 - 6 Marks)
Ans. Sol. The given circle is 2x (x – a) + y (2y – b) = 0 (a, b ≠ 0)
⇒ 2x2 + 2y2 – 2ax – by = 0 ....(1)
Let us consider the chord of this circle which passes through
the pt 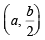 and whose mid pt. lies on x-axis.
and whose mid pt. lies on x-axis.

Let (h, 0) be the mid point of the chord, then eq. of chord can be obtained by T = S1
i.e., 2xh + 2y.0 – a (x + h) – 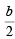 (y + 0) = 2h2 – 2ah
(y + 0) = 2h2 – 2ah
⇒ (2h – a) x – 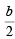 y + ah – 2h2 = 0
y + ah – 2h2 = 0
This chord passes through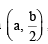 therefore
therefore
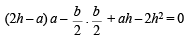
⇒ 8h2 – 12ah + (4a2 + b2) = 0
As given in question, two such chords are there, so we should have two real and distinct values of h from the above quadratic in h, for which
D > 0
⇒ (12a)2 – 4 × 8 × (4 a2 + b2) > 0
⇒ a2 > 2b2
Q.13. Consider a family of circles passing through two fixed points A (3,7) and B (6, 5). Show that the chords in which the circle x2 + y2 – 4x – 6y – 3 = 0 cuts the members of the family are concurrent at a point. Find the coordinate of this point. (1993 - 5 Marks)
Ans. 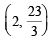
Sol. Let the family of circles, passing through A (3, 7) and B (6, 5), be
x2 + y2 + 2gx + 2fy + c = 0
As it passes through (3, 7)
∴ 9 + 49 + 6g + 14f + c = 0 or,6g + 14f + c + 58 = 0 … (1)
As it passes through (6, 5)
∴ 36 + 25 + 12g + 10f + c = 0
12g + 10f + c + 61 = 0 … (2)
(2) – (1) gives,
6g – 4f + 3 = 0 
Substituting the value of g in equation (1),
we get 4f – 3 + 14f + c + 58 = 0
⇒ 18f + 55 + c = 0 ⇒ c = – 18f – 55
Thus the family is
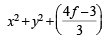 x + 2fy – (18f + 55) = 0
x + 2fy – (18f + 55) = 0
Members of this family are cut by the circle x2 + y2 – 4x – 6y – 3 = 0
∴ Equation of family of chords of intersection of above two circles is S1 – S2 = 0
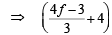 x + (2f + 6) y – 18f + 52) = 0
x + (2f + 6) y – 18f + 52) = 0
which can be written as
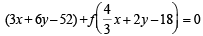
which represents the family of lines passing through the pt. of intersection of the lines
3x + 6y – 52 = 0 and 4x + 6y – 54 = 0
Solving which we get x = 2 and y = 23/3.
Thus the required pt. of intersection is 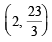
Q.14. Find the coordinates of the point at which the circles x2 + y2 – 4x – 2y = –4 and x2 + y2 – 12x – 8y = – 36 touch each other. Also find equations common tangents touching the circles in the distinct points. (1993 - 5 Marks)
Ans. Sol. The given circles are
x2 + y2 – 4x – 2y = – 4 and
x2 + y2 – 12x – 8y = – 36
i.e., x2 + y2 – 4x – 2y + 4 = 0 … (1)
x2 + y2 – 12x – 8y + 36 = 0 .... (2)
with centres C1(2, 1) and C2 (6, 4) and radii 1 and 4 respectively.
Also C1C2 = 5 As r1 + r2 = C1C2
⇒ Two circles touch each other externally, at P.
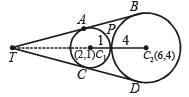
Clearly, P divides C1C2 in the ratio 1 : 4
∴ Co-ordinates of P are
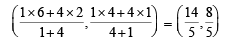
Let AB and CD be two common tangents of given circles, meeting each other at T. Then T divides C1C2 externally in the ratio 1 : 4.
KEY CONCEPT : [As the direct common tangents of two circles pass through a pt. which divides the line segment joining the centres of two circles externally in the ratio of their radii.]
Hence,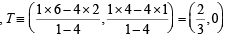
Let m be the slope of the tangent, then equation of tangent through (2/3, 0) is
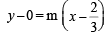
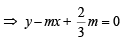
Now, length of perpendicular from (2, 1), to the above tangent is radius of the circle
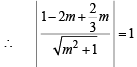
⇒ (3 – 4m)2 = 9(m2 + 1) ⇒ 9 – 24m + 16m2 = 9m2 + 9
⇒ 7m2 – 24m = 0 ⇒ m = 0,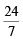
Thus the equations of the tangents are y = 0 and 7y – 24x + 16 = 0.
Q.15. Find the intervals of values of a for which the line y + x = 0 bisects two chords drawn from a point 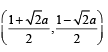 to the circle 2x2 + 2y2 -
to the circle 2x2 + 2y2 -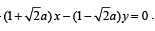 (1996 - 5 Marks)
(1996 - 5 Marks)
Ans.
Sol. Let the given point be
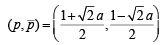 and the equation of the circle
and the equation of the circle
becomes x2 + y2 – px – 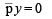
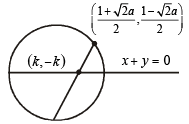
Since the chord is bisected by the line x + y = 0, its mid-point can be chosen as (k, – k). Hence the equation of the chord by T = S1 is
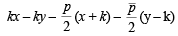
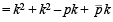
It passes through 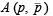
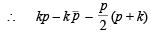
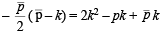
or 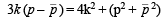 … (1)
… (1)
Put 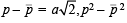
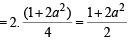 … (2)
… (2)
Hence, from (1) by the help of (2), we get
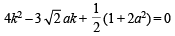 … (3)
… (3)
Since, there are two chords which are bisected by x + y = 0, we must have two real values of k from (3)
∴ Δ > 0
or 18a2 – 8 (1 + 2a2) > 0
or,a2 – 4 > 0
or,(a + 2) (a – 2) > 0
∴ a < – 2 or > 2
∴ a ∈ (– ∞, – 2) ∪ (2, ∞)
or a ∈ ] – ∞, –2[ ∪ ] 2, ∞ [
Q.16. A circle passes through three points A, B and C with the line segment AC as its diameter. A line passing through A intersects the chord BC at a point D inside the circle. If angles DAB and CAB are α and β respectively and the distance between the point A and the mid point of the line segment DC is d, prove that the area of the circle is
 (1996 - 5 Marks)
(1996 - 5 Marks)
Ans.
Sol. Let r be the radius of circle, then AC = 2r Since, AC is the diameter
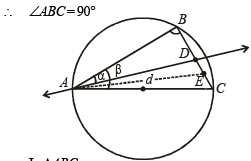
∴ In ΔABC BC = 2r sinβ, AB = 2r cosβ
In rt ∠ed ΔABC BD = AB tanα = 2r cosβ tanα
AD = AB secα = 2r cosβ secα
∴ DC = BC – BD = 2r sinβ – 2r cosβ tanα
Now since E is the mid point of DC
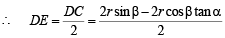
⇒ DE = r sinβ – r cosβ tanα Now in ΔADC, AE is the median
∴ 2 (AE2 + DE2) = AD2 + AC2
⇒ 2 [d2 + r2 (sinβ – cosβ tanα)2]
= 4r2 cos2 b sec2 a + 4r2
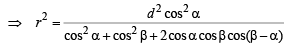
⇒ Area of circle,
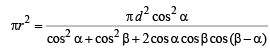
Q.17. Let C be any circle with centre (0, 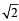 ) . Prove that at the most two rational points can be there on C. (A rational point is a point both of whose coordinates are rational numbers.) (1997 - 5 Marks)
) . Prove that at the most two rational points can be there on C. (A rational point is a point both of whose coordinates are rational numbers.) (1997 - 5 Marks)
Ans.
Sol. Given C is the circle with centre at (0, 2 ) and radius r (say) then 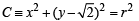
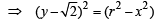
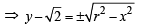
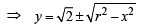 … (1)
… (1)
The only rational value which y can have is 0.
Suppose the possible value of x for which y is 0 is x1. Certainly – x1 will also give the value of y as 0 (from (1)).
Thus, at the most, there are two rational pts which satisfy the eqn of C.
Q.18. C1 and C2 are two concentric circles, the radius of C2 being twice that of C1. From a point P on C2, tangents PA and PB are drawn to C1. Prove that the centroid of the triangle PAB lies on C1. (1998 - 8 Marks)
Ans.
Sol. Let P (h, k) be on C2
∴ h2 + k2 = 4r2
Chord of contact of P w.r.t. C1 is hx + ky = r2
It intersects C1, x2 + y2 = a2 in A and B.
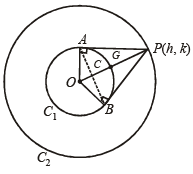
Eliminating y, we get,
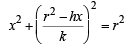
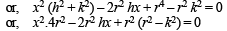
If (x, y) be the centroid of ΔPAB, then
 or h = 2x and similarly k = 2y
or h = 2x and similarly k = 2y
Putting in (1) we get 4x2 + 4y2 = 4r2
∴ Locus is x2 + y2 = r2 i.e., C1
Q.19. Let T1, T2 be two tangents drawn from (–2, 0) onto the circle C : x2 + y2 = 1. Determine the circles touching C and having T1, T2 as their pair of tangents. Further, find the equations of all possible common tangents to these circles, when taken two at a time. (1999 - 10 Marks)
Ans.
Sol. The given circle is x2 + y2 = 1 … (1)
Centre O (0, 0) radius = 1
Let T1 and T2 be the tangents drawn from (– 2, 0) to the circle (1).
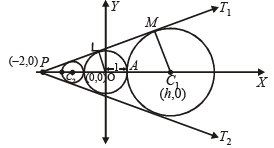
Let m be the slope of tangent then equations of tangents are
y – 0 = m (x + 2) or, mx – y + 2m = 0 … (2)
As it is tangent to circle (1)
length of ⊥ lar from (0, 0) to (2) = radius of (1)
 4m2 = m2 + 1 ⇒ m
4m2 = m2 + 1 ⇒ m 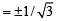
∴ Th e two tangen ts are 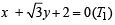 and
and
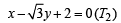
Now any other circle touching (1)
and T1, T2 is such that its centre lies on x-axis.
Let (h, 0) be the centre of such circle, then from fig.
OC1 = OA + AC1 ⇒ | h | = 1 + | AC1 |
But AC1 = ⊥ lar distance of (h, 0) to tangent
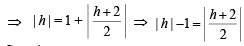
Squaring,
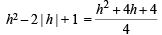
⇒ 4h2 ± 8h + 4 = h2 + 4h + 4
‘ + ’ ⇒ 3h2 = – 4h ⇒ h = – 4/3
‘–’ ⇒ 3h2 = 12h ⇒ h = 4
Thus centres of circles are (4, 0),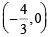
∴ Radius of circle with centre (4, 0) is = 4 – 1 = 3 and radius of circle with centre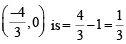
∴ The two possible circles are (x – 4)2 + y2 = 32 … (3)
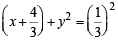 … (4)
… (4)
Now, common tangents of (1) and (3). Since (1) and (3) are two touching circles they have three common tangents
T1, T2 and x = 1 (clear from fig.)
Similarly common tangents of (1) and (4) are T1, T2 and x = – 1.
For the circles (3) and (4) there will be four common tangents of which two are direct common tangents .
XY and x' y' and two are indirect common tangents. Let us find two common indirect tangents. We know that In two similar Δ’s C1XN and C2YN
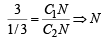 divides C1C2 in the ratio 9 : 1.
divides C1C2 in the ratio 9 : 1.
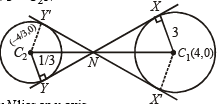
Clearly N lies on x-axis.
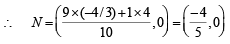
Any line through N is
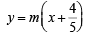 or 5mx – 5y + 4m = 0
or 5mx – 5y + 4m = 0
If it is tangent to (3) then
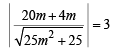
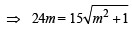 ⇒ 64m2 = 25m2 + 25
⇒ 64m2 = 25m2 + 25
⇒ 39m2 = 25 ⇒ 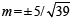
∴ Required tangents are
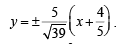
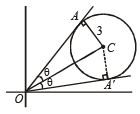
Q.20. Let 2x2 + y2 - 3xy = 0 be the equation of a pair of tangents drawn from the origin O to a circle of radius 3 with centre in the first quadrant. If A is one of the points of contact, find the length of OA. (2001 - 5 Marks)
Ans. Sol. The equation 2x2 – 3xy + y2 = 0 represents pair of tangents OA and OA'.
Let angle between these to tangents be 2θ.
Then, 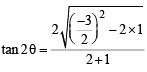
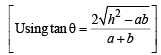
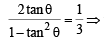
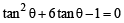
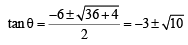
As θ is acute 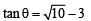
Now we know that line joining the pt through which tangents are drawn to the centre bisects the angle between the tangents,
∴∠AOC = ∠A'OAC = θ
In ΔAOC,
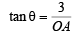
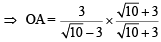
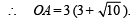
Q.21. Let C1 and C2 be two circles with C2 lying inside C1. A circle C lying inside C1 touches C1 internally and C2 externally.
Identify the locus of the centre of C. (2001 - 5 Marks)
Ans. Sol. Let equation of C1 be x2 + y2 = r12 and of C2 be
(x – a)2 + (y – b)2 = r22
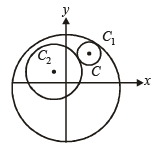
Let centre of C be (h, k) and radius be r, then by the given conditions.
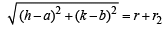 and
and 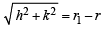
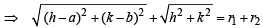
Required locus is
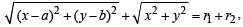
which represents an ellipse whose foci are at (a, b) and (0, 0).
[∵ PS + PS' = constant ⇒ locus of P is an ellipse with foci at S and S']
Q.22. For the circle x2 + y2 = r2, find the value of r for which the area enclosed by the tangents drawn from the point P (6, 8) to the circle and the chord of contact is maximum. (2003 - 2 Marks)
Ans.
Sol. The given circle is x2 + y2 = r2
From pt. (6, 8) tangents are drawn to this circle.

Then length of tangent
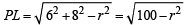
Also equation of chord of contact LM is
6x + 8y – r2 = 0
PN = length of ⊥ lar from P to LM
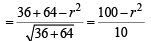
Now in rt. ΔPLN, LN2 = PL2 – PN2
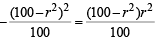
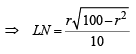
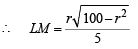 (∵ LM = 2 LN)
(∵ LM = 2 LN)
∴ Area of ΔPLM =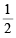 x L M x PN
x L M x PN
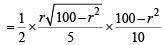
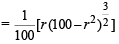
For max value of area, we should have
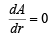
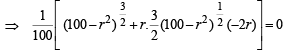
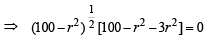
⇒ r = 10 or r = 5
But r = 10 gives length of tangent PL = 0
∴ r ≠ 10. Hence, r = 5
Q.23. Find the equation of circle touching the line 2x + 3y + 1 = 0 at (1, – 1) and cutting orthogonally the circle having line segment joining (0, 3) and (–2, –1) as diameter. (2004 - 4 Marks)
Ans. Sol. We are given that line 2x + 3y + 1 = 0 touches a circle S = 0 at (1, – 1).
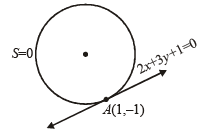
So, eqn of this circle can be given by (x – 1)2 + (y + 1)2 + λ(2x + 3y + 1) = 0.
[Note : (x – 1)2 + (y + 1)2 = 0 represents a pt. circle with centre at (1, –1)].
or x2 + y2 + 2x (λ – 1) + y (3λ + 2) + (λ + 2) = 0 …(1)
But given that this circle is orthogonal to the circle, the extremities of whose diameter are (0, 3) and (– 2, – 1)
i.e. x (x + 2) + (y – 3) (y + 1) = 0
x2 + y2 + 2x – 2y – 3 = 0 .......... (2)
Applying the condition of orthogonality for (1) and (2), we
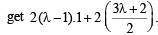
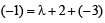
[2g1g2 + 2f1f2 = c1 + c2]
⇒ 2λ – 2 – 3λ – 2 = λ – 1
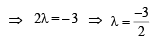
Substituting this value of λ in eqn (1) we get the required circle as
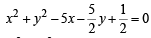
or,2x2 + 2y2 – 10x – 5y + 1 = 0
Q.24. Circles with radii 3, 4 and 5 touch each other externally. If P is the point of intersection of tangents to these circles at their points of contact, find the distance of P from the points of contact. (2005 - 2 Marks)
Ans. Sol. Given these circles with centres at C1, C2 and C3 and with radii 3, 4 and 5 respectively, The three circles touch each other externally as shown in the figure.
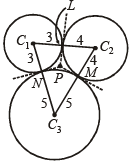
P is the point of intersection of the three tangents drawn at the pts of contacts, L, M and N. Since lengths of tangents to a circle from a point are equal, we get
PL = PM = PN
Also PL ⊥ C1C2 , PM ⊥ C2C3, PN⊥ C1C3
(Q tangent is perpendicular to the radius at pt. of contact)
Clearly P is the incentre of ΔC1C2C3 and its distance from pt.of contact i.e.,
PL is the radius of incircle of ΔC1C2C3.
In ΔC1C2C3 sides are a = 3 + 4 = 7, b = 4 + 5 = 9, c = 5 + 3 = 8
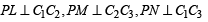
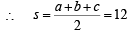
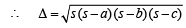
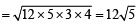
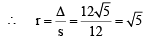
|
446 docs|930 tests
|

















