Integer Answer Type Questions: Definite Integrals and Applications of Integrals | JEE Advanced | 35 Years Chapter wise Previous Year Solved Papers for JEE PDF Download
Q. 1. Let f: R → R be a continuous function which satisfies (2009)
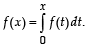
Then the value of f (ln 5) is (2009)
Ans. 0
Solution.
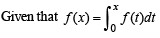
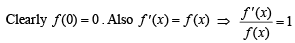
Integrating both sides with respect to x, we get
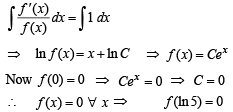
Q. 2. For any real number x, let [x] denote the largest integer less than or equal to x. Let f be a real valued function defined on the interval [–10, 10] by
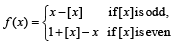
Then the value of 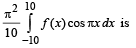 (2010)
(2010)
Ans. 4
Solution.
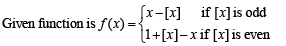
The graph of this function is as below
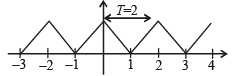
Clearly f(x) is periodic with period 2
Also cos πx is periodic with period 2
∴ f ( x) cosπx is periodic with period 2
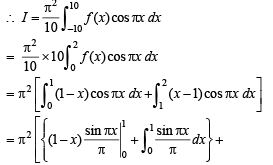
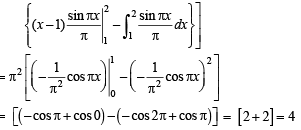
Q. 3. 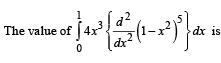 (JEE Adv. 2014)
(JEE Adv. 2014)
Ans. 2
Solution.
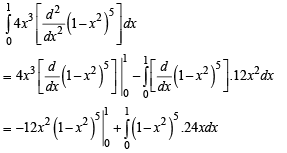
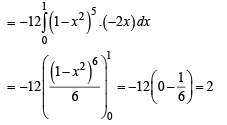
Q. 4. Let f : R → R be a function defined by 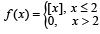 where [x] is the greatest integer less than or equal to x, if
where [x] is the greatest integer less than or equal to x, if 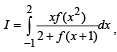 , then the value of (4I – 1) is (JEE Adv. 2015)
, then the value of (4I – 1) is (JEE Adv. 2015)
Ans. 0
Solution.
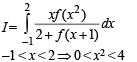
Also 0 < x2 < 1 ⇒ f(x2) = [x2] = 0
1 < x2 < 2 ⇒ f(x2) = [x2] = 1
2 < x2 < 3 ⇒ f(x2) = 0 (using definition of f)
3 < x2 < 4 ⇒ f(x2) = 0 (using definition of f)
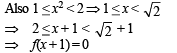
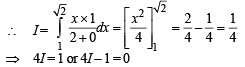
Q. 5. Let 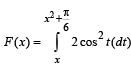 for all x ∈ R and
for all x ∈ R and 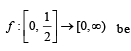 a continuous function. F or
a continuous function. F or 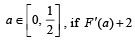 is the area of the region bounded by x = 0, y = 0, y = f(x) and x = a, then f(0) is (JEE Adv. 2015)
is the area of the region bounded by x = 0, y = 0, y = f(x) and x = a, then f(0) is (JEE Adv. 2015)
Ans. 3
Solution.
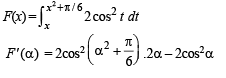
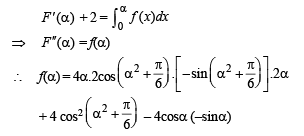
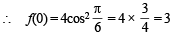
Q. 6. 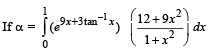 where tan–1x takes only principal values, then the value of
where tan–1x takes only principal values, then the value of 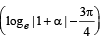 is (JEE Adv. 2015)
is (JEE Adv. 2015)
Ans. 9
Solution.
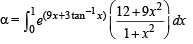
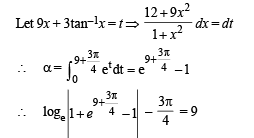
Q. 7. 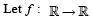 be a continuous odd function, which vanishes exactly at one point and f (1) = 1/2. Suppose that
be a continuous odd function, which vanishes exactly at one point and f (1) = 1/2. Suppose that 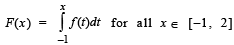
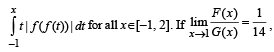 then the value of
then the value of 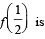 (JEE Adv. 2015)
(JEE Adv. 2015)
Ans. 7
Solution.
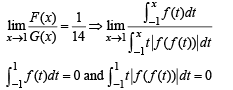
f(t) being odd function
∴ Using L Hospital’s rule, we get
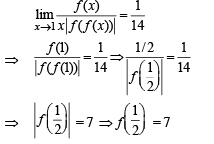
Q. 8. The total number of distinct x ∈ [0, 1] for which  (JEE Adv. 2016)
(JEE Adv. 2016)
Ans. 1
Solution.
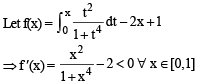
∴ f is decreasing on [0, 1]
Also f(0) = 1
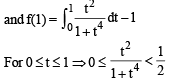
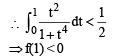
∴ f(x) crosses x-axis exactly once in [0, 1]
∴ f(x) = 0 has exactly one root in [0, 1]
|
347 docs|185 tests
|
FAQs on Integer Answer Type Questions: Definite Integrals and Applications of Integrals - JEE Advanced - 35 Years Chapter wise Previous Year Solved Papers for JEE
| 1. What is a definite integral? |  |
| 2. How is a definite integral calculated? |  |
| 3. What are the applications of definite integrals? |  |
| 4. How can definite integrals be used to calculate areas? |  |
| 5. Can definite integrals be used to solve real-world problems? |  |
















